一道八年级数学试题的溯源、解答及推广
广东省广州市真光中学(510380) 苏国东
2020年广州市荔湾区八年级上学期期末考第25 题基于熟悉情境命制,层次分明,方法灵活,推广性强,是对一学期几何模块知识的整合与提升.试题集中考查了等边三角形和全等三角形的判定与性质,添加辅助线构造几何模型,分类讨论、类比与转化等数学思想.要求学生具备较好的直观想象、数学建模、逻辑推理等核心素养,以及分析、解决动态问题的思维能力.
1 试题呈现
试题:已知ΔABC为等边三角形,点D、E分别是边AB、BC所在直线上的动点,若点D、E以相同的速度,同时从点A、点B出发,分别延AB、BC方向运动,直线AE、CD交于点O.
(1)如图1,求证:ΔABE∽= ΔCAD;

图1
(2)在点D、点E运动过程中,∠COE=____°;
(3)如图2,点P为边AC中点,连接BO、PO,当点D、E分别在线段AB、BC上运动时,判断BO与PO的数量关系,并证明你的结论.

图2
2 试题溯源
通过对试题及图形的拆分与还原,可知(1)(2)是以等边三角形为基本模型,以动态问题为背景,考查熟悉的全等与角度的问题,源于以下中考压轴题.
素材1:(2020年四川凉山中考第25 题)点P、Q分别是等边ΔABC边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图3,连接AQ、CP,求证:ΔABQ∽= ΔCAP;
(2)如图3,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,∠QMC的大小是否变化? 若变化,请说明理由;若不变,求出它的度数;

图3
(3)如图4,当点P、Q在AB、BC的延长线上运动时,直线AQ、CP相交于点M,∠QMC的大小是否变化? 若变化,请说明理由;若不变,求出它的度数.
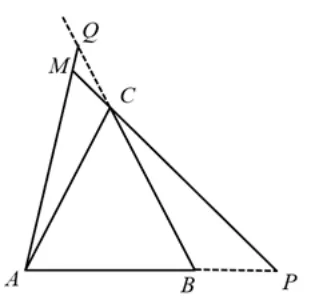
图4
命题者将素材后两问精简为试题(2)的填空题,降低门槛,为试题(3)的解答留出空间.试题(3)以等边三角形为背景,意在考查添加辅助线构造手拉手模型和倍长中线模型,将条件转化和集中到各组全等三角形当中.本问源于以下期末考压轴题.
素材2:(2017年武汉武昌期末考第24 题节选)如图5,ΔABC为等边三角形,点M是BC中点,点P是ΔABC内一点,连接PA,PB,PC,PM,直线PC与直线AB交于点D,∠BPC=120°.
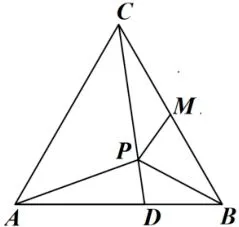
图5
(1)当点P在AM上时,求证:∠APD=∠BPM;
(2)当点P不在AM上时,∠APD=∠BPM是否仍然成立? 若成立,请证明;若不成立,请说明理由.
素材2 中的∠BPC=120°可转换为∠BPD=60°,与素材1 中的∠QMC= ∠AMP= 60°实现无缝对接.命题者选取素材题(2)的一般情形,将构造全等三角形证明的对应角关系,结合中点的条件替换为证明对应边的数量关系,即PA=2PM,以吻合压轴题(3)的命题难度.
最后,整合问题与图形,统一编排字母,试题命制成型.
3 试题解答
(1)如图1,因为ΔABC为等边三角形,所以AB=AC,∠ABE= ∠CAD= 60°,又因为点D、E运动速度相同,故AD=BE,所以ΔABE∽= ΔCAD.
(2) 分为两动点在线段或其延长线上运动两种情况.情况1:当点D、E分别在线段AB、BC上运动时,由ΔABE∽= ΔCAD可得∠EAB= ∠ACD,所以∠COE=∠CAE+ ∠ACD= ∠CAE+ ∠EAB= ∠CAB= 60°;情况2:当点D、E分别在AB、BC的延长线上运动时,如图6.仍有AB=AC,∠ABE= ∠CAD= 60°,AD=BE,所以ΔABE∽= ΔCAD,故∠AEB= ∠ADC,所以∠COE= ∠OAD+ ∠ADC= ∠OAD+ ∠AEB=∠EBD= 180° -∠ABC= 180° -60°= 120°.综上所述,∠COE为60°或120°.

图6
(3)需要再构造一个等边三角形以建立手拉手模型,可将OA或OC绕点O顺时针或逆时针旋转60°进行构造.下面各举一种解法.
解法1:如图7,将OA绕点O逆时针旋转60°得到ON,因为∠COE= 60°,所以C、O、N三点共线.连接AN、BN,易知ΔAON是等边三角形,所以OA=AN=ON,∠OAN= ∠ONA= 60°.因 为∠CAB= 60°,所以∠CAO= ∠BAN.又因为AB=AC,所以ΔACO∽= ΔABN,CO=BN,∠ANB= ∠AOC=180°-∠COE=120°,所以∠BNO=60°.
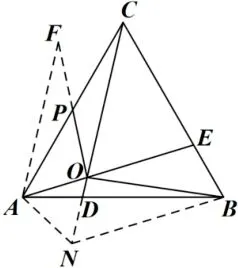
图7
延长OP至点F,使得PF=PO,连接AF.因为点P是边AC的中点,所以PA=PC,易证ΔCPO∽= ΔAPF,所以AF=CO=BN,∠PAF= ∠PCO,所以CO//AF,∠FAO= ∠COE= 60°= ∠BNO.又因为OA=ON,所以ΔAOF∽= ΔNOB,BO=FO=2PO.
解法2:如图8,将OC绕点O顺时针旋转60°得到ON,因为∠COE=60°,所以O、E、N三点共线.连接CN、BN,易知ΔCON是等边三角形,OC=ON=CN,∠OCN=∠ONC=60°.因为∠ACB=60°,所以∠ACO=∠BCN.又因为AC=BC,所以ΔACO∽= ΔBCN,AO=BN,∠BNC=∠AOC=180°-∠COE=120°,所以∠BNO=60°.

图8
延长OP至点F,使得PF=PO,连接AF.因为点P是边AC的中点,所以PA=PC,易证ΔCPO∽= ΔAPF,所以AF=CO=ON,∠PAF= ∠PCO,所以CO//AF,∠FAO=∠COE=60°=∠BNO.
又因为AO=BN,所以ΔAOF∽= ΔNBO,BO=FO=2PO.
4 变式推广
根据素材2,在最后证得的两个全等三角形中,对应角之间也存在相等关系,故有推广1.
推广1:在(3)中,判断∠AOP与∠BOD(或∠POC与∠BOE)的数量关系,并证明你的结论.
在(2)解答的情况2 中,直线AE、CD的交点O移至了ΔABC外部,可探究此时上述线段或角度之间的数量关系是否仍成立,故有推广2.
推广2:如图9,当点D、E分别在AB、BC的延长线上运动时,判断BO与PO的数量关系,以及∠AOP与∠BOD的数量关系,并证明你的结论.

图9
更一般的,当点O在等边ΔABC外部,满足∠AOC=60°时,即可探究上述线段和角度是否存在确定的数量关系,即有推广3.
推广3:ΔABC为等边三角形,点O与点B位于直线AC的两侧,且∠AOC=60°,直线AB、CO交于点D,点P为边AC中点,连接BO、PO.判断BO与PO的数量关系,以及∠AOP与∠BOD的数量关系,并证明你的结论.
虽然图形发生了改变,但解题思路和构造方式可作类比引申.下面以推广3 为例进行解答.
解:显然点D在AB的延长线或反向延长线上.
情况1:当点D在AB延长线上时,如图10,将OA绕点O逆时针旋转60°得到ON,因为∠AOC= 60°,所以O、C、N三点共线.连接AN、BN,易知ΔAON是等边三角形,AO=AN=ON,∠OAN= ∠ONA= 60°.因为∠CAB= 60°,所以∠OAC= ∠NAB.又因为AC=AB,所以ΔAOC∽= ΔANB,OC=NB,∠ANB= ∠AOC=60°,所以∠ONB=120°.

图10
延长OP至点F,使得PF=PO,连接AF.因为点P是边AC的中点,所以PA=PC,易证ΔAPF∽= ΔCPO,所以AF=OC=NB,∠PAF= ∠PCO,所以AF//OC,∠OAF=180°-∠AOC=120°=∠ONB.
又因为OA=ON,所以ΔOAF∽= ΔONB,BO=OF=2PO,∠AOP=∠BOD.
此情况1 也即为推广2 的解答.
情况2:当点D在BA延长线上时,如图11,将OC绕点O顺时针旋转60°得到ON,因为∠AOC= 60°,所以O、A、N三点共线.连接CN、BN,易知ΔCON是等边三角形,OC=ON=CN,∠OCN= ∠ONC= 60°.因为∠ACB= 60°,所以∠OCA= ∠NCB.又因为AC=BC,所以ΔACO∽= ΔBCN,OA=NB,∠BNC= ∠AOC=60°,所以∠ONB=120°.

图11
延长OP至点F,使得PF=PO,连接CF.因为点P是边AC的中点,所以PA=PC,易证ΔOPA∽= ΔFPC,所以CF=OA=NB,∠POA= ∠PFC,所以AO//CF,∠OCF=180°-∠AOC=120°=∠ONB.
又因为OC=ON,所以ΔOCF∽= ΔONB,BO=FO= 2PO,∠COF= ∠NOB,所以∠AOP= ∠BOC,所以∠AOP+∠BOD=∠BOC+∠BOD=180°.
综上所述,BO= 2PO,∠AOP= ∠BOD或∠AOP+∠BOD=180°.

