搭建问题的桥梁 实现思维的联通——以圆的习题课为例

广州市白云区金沙小学(510168) 吴厚仪

数学教学的根本目标,是培养学生的数学思维.而数学思想方法作为数学的“灵魂”,在培养学生数学思维的过程中起决定性作用.因此,数学思想方法的传授是数学教学过程的核心.然而,数学基本思想方法总是被掩盖在教材所呈现的概念、定理等具体数学知识的背后,看不见、摸不着.在数学课堂上,教师如何在教材知识和数学问题的讲解过程中,做到“不着痕迹”地传授数学思想方法,潜移默化地培养学生的数学思维? 本文从一节圆的习题课出发,探讨教师如何在数学习题课上为学生提供数学思维策略的指导和数学思想方法的传授,让学生在逐步感悟数学思想方法的过程中,提升数学思维.

1 教学过程

《义务教育数学课程标准(2011年版)》中强调,学生在积极参与教学活动的过程中,通过独立思考、合作交流,逐步感悟数学思想.本课例中,笔者将从“初探问题——再探问题——总结归纳——方法应用——拓展深化”五个环节开展教学活动.

1.1 初探问题

例1如图1,AB是⊙O的直径,CD是⊙O的一条弦.求证:∠BCO=∠D.

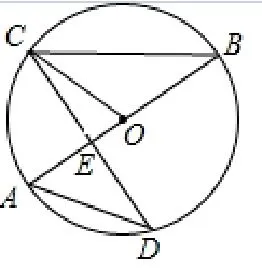
图1

例2如图2,在ΔABC中,∠ACB= 90°,以BC为直径的圆O交AB于点D.

图2

求证:∠ACD=∠DEC.

例3如图3,AB是⊙O的直径,点C、F在⊙O上,CD⊥AB,垂足为D,CD的延长线交BF于点E,求证:∠BCE=∠BFC.

图3

1.2 再探问题

问题1:请分别讲解这三道例题的解题思路.

问题2:这三道例题有没有共通点? (提示:可从条件、设问、解题思路等方面出发进行思考)

【教学片断】

师:刚刚三位同学都不约而同地从知识点这个角度来分析解题思路的共通点,为大家总结了以后在遇到这类问题的时候,应该首先联想到哪些知识点进行解决.很实用的总结!那么除了知识点以外,这三道题在解题方法上有没有共通点呢?

(生静静思考,似乎没有答案)

师:在这三道例题里,我们能不能直接证明设问里所提出的两个角相等呢?

生(齐声答):不能.

师:既然无法直接证明,那么我们是如何间接证明的?

生1:例如说,题目要求我们证明∠1 = ∠2,我们先分别证明∠1 和∠2 都等于∠3,这样就可以运用等量代换,得到∠1=∠2.

生2:或者说先分别证明∠1 = ∠3,∠2 = ∠4,然后再证明∠3=∠4,最后可以通过等量代换,得到这四个角相等.

师:也就是说,由于无法直接证明两个角相等,所以我们借助了∠3 甚至是∠4 的力量,然后运用了等量代换的方法证明是吗?

生(齐声答):是的.

师:在等量代换的过程中,引入的∠3 和∠4 起到了什么作用?

生9:被代换的等量.

师:是的! 它们就像一座鹊桥一样,让两边需要证明相等的∠1 和∠2 牵起了双手,结成一段良缘,然后默默退出,深藏功与名.

(生开心地笑了)

师:所以,我们在发现“证明∠1 = ∠2”这一问题无法一下子解决时,我们就考虑引入∠3,把问题退一步,转化为先证明∠1 = ∠3,∠2 = ∠3,最后运用等量代换得到∠1=∠3=∠2,搭建∠3 这座桥梁把∠1 和∠2 牵起来.搭建桥梁的这一过程,不仅仅运用了等量代换的方法,更重要地是,它体现了一种数学基本思想方法——转化与化归.

1.3 总结归纳

转化与化归思想,就是在解决数学问题时通过观察、联想、等价转化等环节,将隐蔽的条件明显化,把未知的问题转化为已知的问题,进而达到解决问题的思想.其中,等量代换就是转化与化归思想的一种重要体现.

【设计意图】

著名数学教育家波利亚在《怎样解题》一书中提出“变化问题”,意即把问题转化为一个等价的问题,去考虑一个可能相关的问题,先解决一个更特殊的问题……“变化问题”揭示了探索解题思路的途径与实质,是波利亚解题思想的精髓.如今,“变化问题”成为重要的数学基本思想方法之一——转化与化归.如何让学生在解决具体数学问题的过程中,领悟体会这一重要的数学思想方法,并逐步内化为一般思维方式? 在本课中,解题完毕后学生再次梳理解题思路,随后教师启发引导学生对三道例题的解题思路进行观察、类比,最终从条件、设问、所用知识方法等多个角度具体分析和归纳其共通点,得出更一般化的解题思想方法.经历分析、观察、类比、总结的过程,学生不仅能逐步培养归纳概括能力和数学表达能力,还能提高数学学习的自我效能感.

另一方面,在教师引导下,学生通过观察、类比、归纳等手段从特殊解法的思路中得到一般解法的信息,这实质是一个解题回顾的过程.解题回顾作为数学解题的基本程序之一,对于数学思维和创造能力的培养有极大的促进作用.教师引导学生进行解题回顾,不仅能提炼和储备解题经验,为数学思维的升华提供经验基础,同时,教师的适时启发和总结归纳以及适量的练习训练,也使学生对于转化与化归这一数学思想方法模糊的感性认识逐步上升为清晰的理性认识.

1.4 方法应用

练习1:如图4,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.求证:DB=DC.

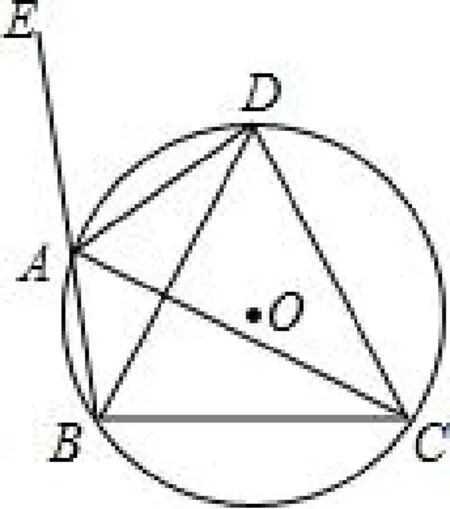
图4

练习2:如图5,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.求证:CF=BF.

图5

1.5 拓展深化

例4如图6,ΔABC中,AB=BC,点O为高AD上一点,以OD为半径的⊙O与AB相切于点E.连接CE,点O在CE上.若AE:EB= 2 :3,AC=求⊙O的半径.

图6

练习:如图7,在ΔABC中,AB=AC,以AB为直径的O分别交BC、AC于点D、E,连接EB交OD于点F.(1)求证:OD⊥BE;(2)若DE=,求AE的长.

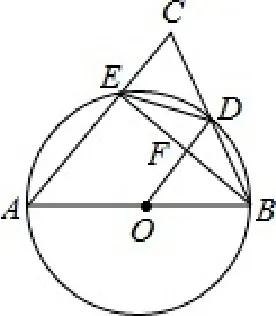
图7

例5(2020年陕西中考):如图8,ΔABC是⊙O的内接三角形,∠BAC= 75°,∠ABC= 45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.(1)求证:AD//EC;(2)若AB= 12,求线段EC的长.

图8

【设计意图】

在圆的问题中,除了角的转化外,还有线段的转化.一类问题是直接进行线段的等量代换,把某一线段作为“桥梁”构建方程进行求解.在例4 中,经过思考不难发现,不论从哪一个直角三角形入手,AD都是问题解决的“挡路石”,为清除这一障碍,不妨考虑转化问题,把“挡路石”变成“垫脚石”.首先在RtΔABD和RtΔACD中,根据勾股定理,分别表示出AD的关系式,然后进行等量代换,将AD作为搭建方程的“桥梁”,进行求解.

另一类问题则是借助辅助线把线段进行平移,把“桥梁”移到所需之处进行问题转化.在例5 第(2)问中,直接求CE比较困难,所以联想到过点A作CE的垂线达到分割CE、平移半径的目的.此时,半径充当了转化问题的“桥梁”,不仅转化为CE的部分已知长度,也成为了利用三角函数求CE未知长度部分的关键.总之,例4、5 的解题过程不仅是圆与三角函数、一元二次方程、勾股定理等内容的拓展与综合,更是转化与化归思想方法运用灵活化与丰富化的体现.

2 总结

2.1 准确把握学生认知结构,激活学生的思维活动

数学是思维的活动,思维的主体性要求人们在学习数学时必须充分发挥自己的主观能动性.数学基本思想方法作为数学家思维活动的精粹,被简明的数学结论所掩盖,要想使其暴露出来,更是离不开学生积极主动的思维活动.如何使学生自发地进行数学思维活动? 首先需要教师准确地把握学生的数学认知结构.一方面,教师只有在充分了解学生数学学习的基础上,才能创造适当的教学情境,引起学生思维的矛盾冲突,从而引起学生的学习兴趣,激发学生积极地进行数学思维活动.另一方面,数学思想方法的高度抽象性与学生的认知发展仍处于从具体到抽象的过渡阶段之间的矛盾,也决定了数学基本思想方法的教学要以学生现有的数学认知水平为基础,以“最近发展区”为定向,才能有效地激发学生的求知欲,促进学生数学思维的发展.

2.2 用心钻研课标和教材,还原专家的思维活动

数学家真实的思维过程蕴含在教材中,但由于学生的认知水平有限,学生独立从教材中揭露数学家的思维活动过程是十分困难的.这就要求教师用心钻研教材和新课程标准,对数学学科整体的知识结构有较完整的把握,并结合专业理论去重新认识、理解教材,注意到数学知识所包含的基本原理,方能深入挖掘出教材背后所掩盖的数学家的思维活动,从而通过思维策略的指导来调控学生的思维活动进程,帮助学生解决矛盾冲突,总结思维规律和方法,潜移默化地引导学生的思维活动向数学家的思维活动靠近,理解数学的本质,运用数学思维和方法分析和解决问题.

2.3 引导学生进行解题回顾,培养数学思维品质

由于中学生的年龄特征以及数学认知结构水平的限制,学生在解答问题以后,往往缺乏对解题过程的反思,不对自己的思维过程进行提炼、概括,为解题而解题,因而解题仅停留在具体经验方法的水平上.如果不对解题的具体方法进行提炼、概括,那么它的适用性就很小,不易产生迁移,不利于数学认知结构灵活性和层次性的提高.因此在学生解题以后,教师必须引导学生结合自己已有的解题经验,回顾整理解题思路,从中归纳概括出一般的、具有广泛应用性的数学思想方法.在教师引导下,学生有层次地对数学思想方法进行概括,使数学思维由个别推广至一般,将解题提高到数学基本思想的熏陶、数学基本方法的训练的层次,这样不仅使学生对数学思想方法的认知不断丰富和深刻,而且有助于学生数学思维品质的提升.

2.4 努力学会稚化思维,实现思维的联通

由于教师与学生在年龄、思维方式、经验丰富程度等方面的差异,教师与学生在数学理解上往往存在较大鸿沟.教师如何能跨越这一鸿沟,在引导学生进行解题回顾的过程中,准确地抓住学生数学思维的盲点和痛点,从而使学生对数学基本思想方法的内化过程更为自然活跃? 关键是教师在启发引导时,要学会稚化思维,即模拟学生的思维方式去分析、思考问题,这样才能明确认识学生在思路寻求的困惑和障碍.然后,教师再以学生的身份展示自然真实的思维过程,努力揭示对方法的思考和选择过程,特别重视对歧途的剖析.如此,教师方能更好地引导学生搭建数学问题的桥梁,促进学生对数学思想方法的内化,实现教师、学生与数学家之间思维的“联通”.