考虑用户参与度的电动汽车集群优化调度策略

韩 妍，丁惜瀛，程 锟，李晓东

（沈阳工业大学，辽宁 沈阳 110870）

0 引言

由于能源紧缺与环境日益恶化，电动汽车的发展已逐渐成为汽车行业的必然趋势。电动汽车不仅清洁、环保，而且其特有的储能能力使其为电网提供辅助服务成为可能。大量电动汽车的储能能力如能得到合理调控，将缓冲电网中可再生能源不确定性带来的影响，有效提高新能源的渗透率[1]。电动汽车负荷具有数量多、容量小、分布散等特点[2]，若被大规模接入电网，则电网调峰将很难控制。将电动汽车分类，以集群的方式调控并网，可有效提升电动汽车规模储能调控的快速性，降低调控难度。在电动汽车并网过程中，电动汽车可被视为移动的储能单元，实现能量在电动汽车与电网之间双向流动[3]。电网负荷低谷期，电动汽车作为负荷充电可避免电能浪费；电网负荷高峰期，电动汽车作为分布式储能电源可缓解电网压力，参与调峰，实现削峰填谷的目的[4-5]。

近年来，电动汽车有序充放电并参与电网调峰一直是行业研究热点。文献[6]利用遗传算法搭建随机参数的电动汽车集群模型，该方法虽理论性强，但不能完全顾及单辆汽车实际情况，因此难以被实际应用。文献[7]根据开始充电时刻和车主期望电量这两个特征值进行电动汽车分类集群，但所考虑的电动汽车集群因素过于单一。文献[8]提出了一种智能有序充电策略，其以电网负荷波动和充电费用最小为优化目标，但并未考虑V2G电动汽车的电网回馈能力。文献[9-10]在对电动汽车进行优化时，仅从电网侧或用户侧进行单方面考量，并没有兼顾双方利益。目前的研究大多基于以电动汽车可用来参与电网调峰的容量为固定值的假设[11]；可实际上，考虑用户意愿以及自身因素，每辆电动汽车参与电网调峰的时段以及可用容量是可以被调控的。根据电网峰谷状态及车辆自身需求，以集群化调控方式确定每辆电动汽车参与调峰的时间段以及可用容量，这将在有效辅助电网调峰的同时降低车辆用电费用。

本文在区域电网电力负荷预测的基础上，综合考虑了电动汽车用户意愿以及电动汽车自身状态，构建了一种基于卷积神经网络的电动汽车集群分类网络，其按调峰参与能力和意愿对电动汽车进行调峰参与度排序并根据排序结果集群化，确定各时段可参与削峰填谷的电动汽车的数量及相关信息；同时考虑电网和用户双方利益，以电网负荷波动和电动汽车用户充放电费用最低为优化目标，采用改进粒子群优化算法计算每个时段的调控容量并进行了仿真验证。

1 电力负荷预测

针对电力负荷预测问题，通过统计产品与服务解决方案（SPSS）仿真平台分别建立了指数平滑法和多层感知器神经网络模型，以预测某区域电网未来一天（24 h）的电力负荷，并进行分析比较。

1.1 指数平滑预测法

指数平滑预测法是通过对一定时间内不规则的电力负荷数据加以平滑处理来确定指数平滑值，从而获取电力负荷数据的变化规律，以此推断和预测未来几天的电力负荷。该方法将所有数据考虑在内并给数据赋予不同权重，其中早期观测值赋予较小的权重，而近期观测值赋予较大权重：

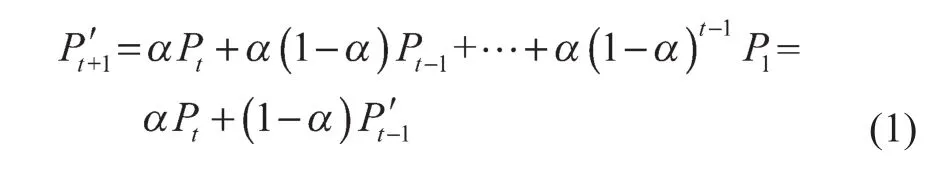
式中：Pt,Pt-1——第t期和第(t-1)期的电力负荷实际值；P′t-1,P′t+1——第(t-1)期和第(t+1)期电力负荷预测值；α——平滑常数，其取值范围为[0, 1]。

采用指数平滑预测法，第（t+1）期电力负荷的单步预测值是以往所有观测值的加权平均数。该方法较为简便，只要有上期实际负荷和预测负荷数据就可预测下期负荷，其无需很多负荷数据并节省处理负荷数据的时间，减小了负荷数据的存储量。

以潍坊青州王母宫地区为例，将预测日前5天每天24 h负荷数据共120个负荷数据依次输入，通过SPSS仿真平台创建传统模型预测未来一天24 h负荷。在所有模型中，选用简单季节性模型进行模型拟合并通过该模型进行预测。模型拟合度统计如表1所示，其中，MAPE表示平均绝对百分比误差，MaxAPE表示最大绝对误差百分比，R²衡量的是模型整体的拟合度。

表1 模型拟合度Tab. 1 Model fit degree

采用指数平滑预测法对该区域进行电力负荷预测，结果如图1所示。

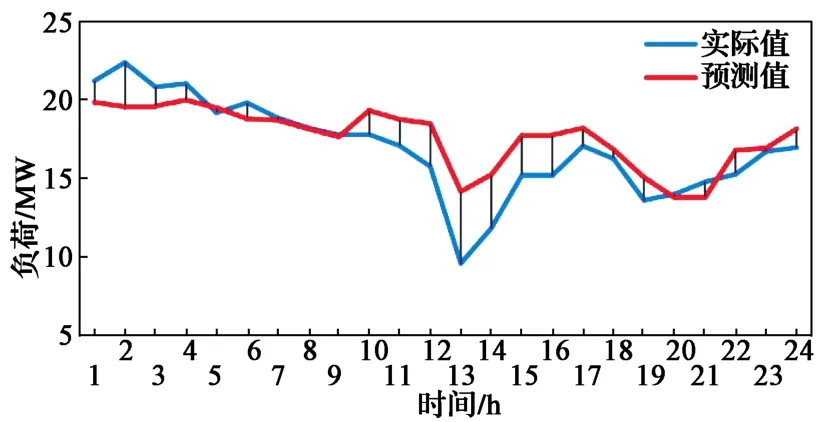
图1 指数平滑预测结果Fig. 1 Exponential smoothing prediction results

在上述模型拟合参数中，R²其值接近于1。可以看出，指数平滑模型对负荷的拟合情况良好，并通过该模型预测未来一天24小时负荷。负荷预测准确率计算公式如式(2)所示。采用指数平滑预测法电力负荷预测准确率为86%。

式中：n——日负荷预测总点数。

1.2 多层感知器神经网络

指数平滑预测法是通过确定平滑常数对未来电力负荷进行预测的，平滑常数过高或过低都会对预测精确度造成一定的影响。多层感知器神经网络是通过学习和训练进行自组织来处理更为复杂的数据，从而提高预测精确度。由于负荷预测模型输入量和输出量较多，因此对模型建立的要求更为严苛，而多层感知器神经网络可通过增加网络层数来提高精度。总体而言，多层感知器神经网络共有3层，分别为输入层、隐含层以及输出层。多层感知器神经网络对隐含层数量以及输出层神经元并没有具体限制，可根据个人需求自行设定，适用面较广。多层感知器神经网络负荷预测模型如图2所示。

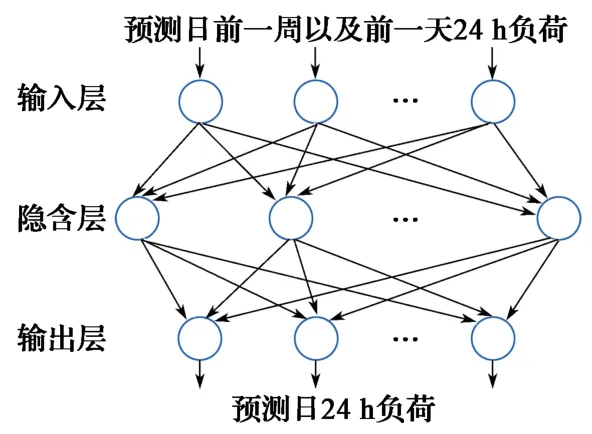
图2 多层感知器神经网络负荷预测模型Fig. 2 Model of load forecasting by multi layer perceptron(MLP)

本文以潍坊青州王母宫地区为例，将预测日前一周以及前一天24 h负荷数据作为神经网络输入，同时将预测日24 h负荷数据作为输出。通过SPSS Modeler仿真平台训练建模（图3），并取500组数据，其中70%用于训练，30%用于测试。

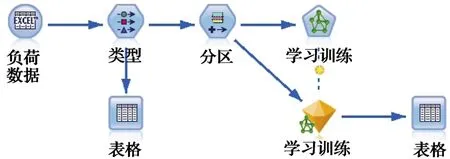
图3 负荷预测建模流程Fig. 3 Load forecasting modeling process

采用多层感知器神经网络与指数平滑预测方法对同一天电力负荷进行预测，结果如图4所示。由图4和式(2)可知，多层感知器神经网络预测准确率达93.6%，相比指数平滑预测法，其预测效果更好。

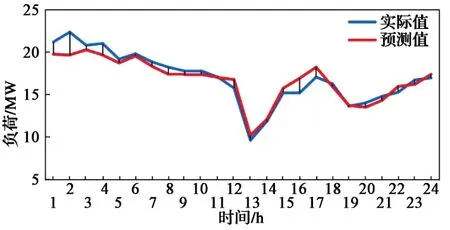
图4 多层感知器神经网络负荷预测结果Fig. 4 Load prediction results by MLP

2 基于卷积神经网络的电动汽车集群

为了充分发挥电动汽车的自身优势、辅助电网削峰填谷，应先对电动汽车进行集群分类。由于电动汽车数据较多，本文选取在处理高维复杂数据方面快速性和准确性较好且便于操作的卷积神经网络进行电动汽车集群分类。

卷积神经网络是一种前馈神经网络，其主要包括卷积层和池化层，结构如图5所示。卷积神经网络不需要任何精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出之间的映射关系，可以在降低数据维度的基础上获取数据深层的特征信息。

图5 卷积神经网络结构Fig. 5 Convolutional neural network structure diagram

应用卷积神经网络将电动汽车进行集群分类，具体流程如下：

（1）生成电动汽车随机数用以模拟电动汽车。随机数涉及车主参与意愿度（0～100%）、距离（0～20 km）、车况良好度（0～100%）、汽车荷电状态SOC（0～100%）、汽车编号（1～50）、百公里耗电量（6～16 kW·h）、实时续航里程（100～900 km）以及额定电池容量（10～100 kW·h）。

（2） 根据规则人为地将电动汽车分为4类，分别为充电（charge）、放电（discharge）、参与调峰（high）以及不参与调峰（low）。电动汽车集群规则如图6所示。

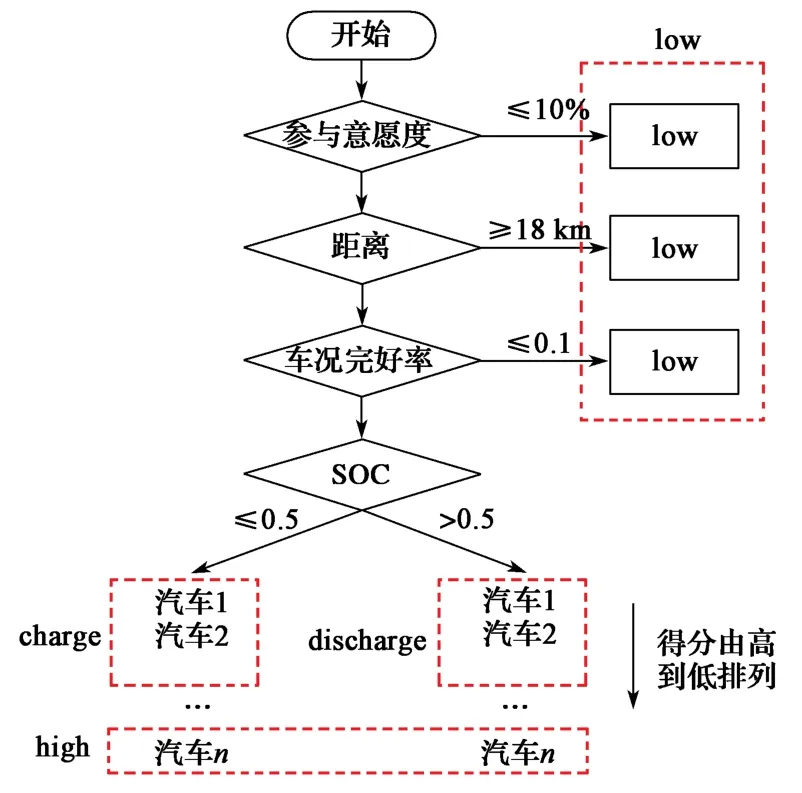
图6 电动汽车集群规则Fig. 6 Electric vehicle cluster rules

具体规则包括车主参与意愿较低、电动汽车距离电站较远或电动汽车自身车况较差（属于不参与调峰的low类）；剩余电动汽车根据荷电状态（SOC）大致分成充电和放电两类，分别按参与调峰可能性由高到低进行排序，根据该时段电网负荷与平均负荷差值大小，取其中排名较高的电动汽车分属于充电charge类和放电discharge类，排名较低的电动汽车属于备选high类。

（3）随机选取1 000组运行数据，其中70%作为训练数据，30%作为验证数据。GoogLenet作为基本神经网络，学习率被设置为1×10-4。训练结果如图7所示。

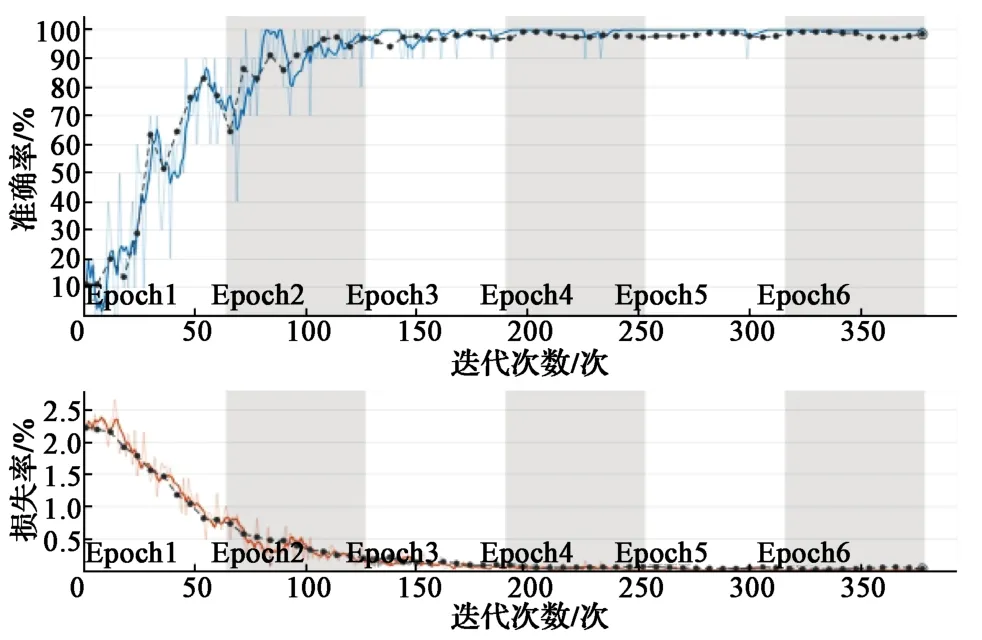
图7 深度学习算法训练结果Fig. 7 DLA training results

由训练结果可知，训练完成后的卷积神经网络平均准确率达到99.17%，用该卷积神经网络对4种集群进行重新验证，各集群判定结果如表2所示。

表2 4类电动汽车集群分类结果准确率Tab. 2 Four types electric vehicles cluster accuracy

由表2可以看出，4类电动汽车集群分类结果准确率均高于90%，具有较高可信度。这表明随着迭代次数的提高，卷积神经网络能有效地根据规则对电动汽车进行集群。对每一时段电动汽车数据进行学习训练，以确定各时段参与调峰的电动汽车的数量及状态信息，进而对可用充放电容量进行优化。

3 参与削峰填谷的电动汽车集群优化调度策略

对电动汽车个体而言，其分布散且容量小，很难对电网产生一定影响；只有以集群形式有序充放电，才能对电网进行有效削峰填谷。本文提出一种以电网侧削峰填谷和用户侧经济效益为目标的电动汽车有序充放电控制策略，并采用改进型粒子群优化算法进行仿真求解，以验证该集群优化调度控制策略的有效性。

3.1 电动汽车集群参与削峰填谷优化调度模型

3.1.1 目标函数

针对电动汽车集群削峰填谷问题，选择未来一天每小时电动汽车集群与电网之间充电和放电的交互功率为优化变量，即{PC1,PC2, …,PCt,PF1,PF2, …,PFt}，其中t=1, 2, …, 24表示24个时间段。

从电网角度考虑，电动汽车集群调度目标是通过调控充放电量来减少负荷波动，使电网平稳运行。以电网负荷曲线的均方差最小为目标函数，构造目标函数F1：

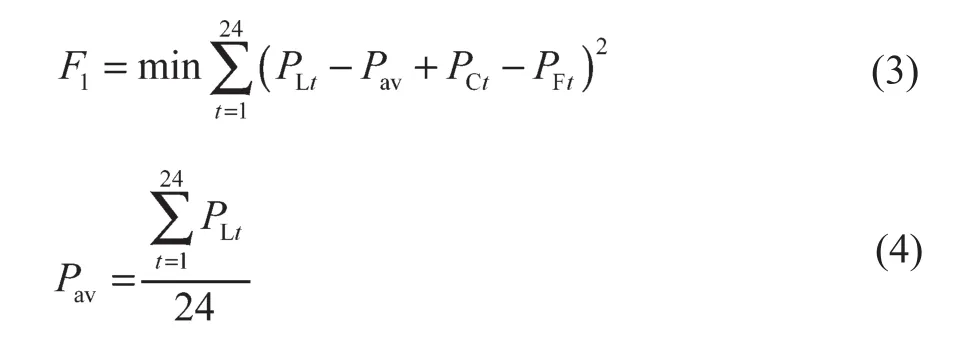
式中：PLt——没有电动汽车时t时段电网的负荷；Pav——没有电动汽车时电网的平均负荷；PCt——电动汽车集群在t时段的充电功率；PFt——电动汽车集群在t时段的放电功率。

从用户角度考虑，根据分时电价用户可以通过分时充电或放电获取更好的经济收益。以用户参与削峰填谷充放电费用最少为目标函数，根据上述优化变量，构造目标函数F2：

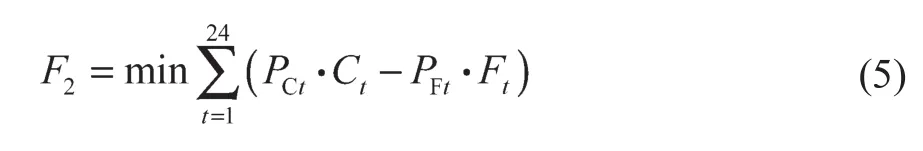
式中：Ct——电动汽车在t时段充电电价；Ft——电动汽车在t时段放电电价。

3.1.2 约束条件

在建立优化目标函数的基础上，还需考虑各种约束条件。电动汽车参与电网调峰受到的约束条件主要为车辆充放电功率、可用荷电状态以及可用容量约束等。

（1）车辆充放电功率约束

电动汽车充放电时，充电电流最大值为额定电流的一半，放电电流最大值为额定电流2倍。

式中：IC——电动汽车的充电电流；IF——电动汽车的放电电流；IN——额定电流，其取决于电池型号。

考虑线路功率容量约束：

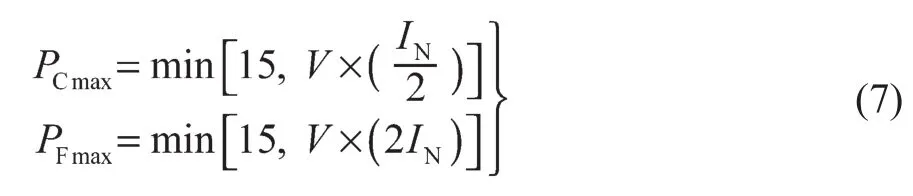
式中：PCmax——电动汽车的充电功率上限；PFmax——电动汽车的放电功率上限；V——电动汽车电压。

（2）可用荷电状态值约束

电池过度充放电会对电动汽车本身造成危害，一般需规定可用荷电状态值范围：

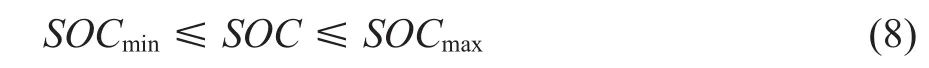
式中：SOCmin——电动汽车电池最低荷电状态；SOCmax——电动汽车电池最高荷电状态。

（3）可用容量约束

根据电动汽车额定容量不同，结合荷电状态上下限，得到电动汽车可用容量约束：

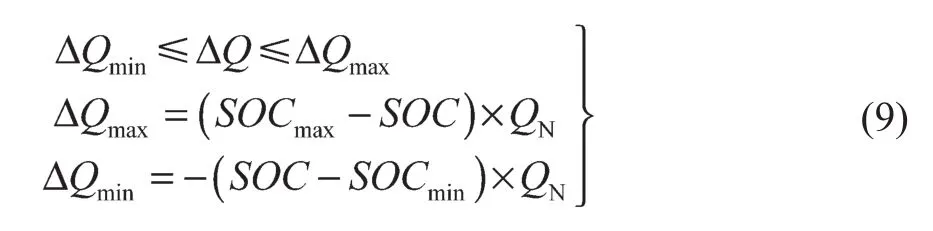
式中：QN——电动汽车额定容量；ΔQmin——电动汽车可用容量下限；ΔQmax——电动汽车可用容量上限。

3.2 粒子群优化算法的改进

3.2.1 粒子权重的设定和改进

标准粒子群算法的速度更新方程为

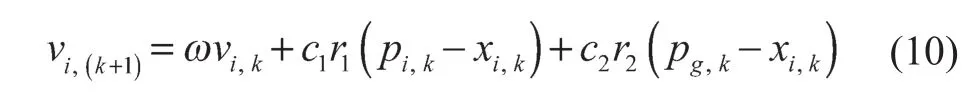
式中：ω——惯性权重；c1,c2——粒子的学习常数；pi——个体极值；pg——全局极值；k——迭代次数；r1,r2——变量，在[0, 1]间均匀取值。

式(10)中，第一部分（ωvi,k）体现局部寻优能力，第二部分（c1r1(pi,k-xi,k)）和第三部分（c2r2(pg,k-xi,k)）体现整体状态下寻优能力，粒子权重的改变会影响全局搜索能力。相比之下，第一部分权重为固定值，此算法在不断迭代时因为权重不变可能会对局部搜索能力产生一定影响，从而影响优化结果。为了更好地解决这个问题，可以将第一部分惯性权重从固定值变为一个动态ω，按式(11)进行取值。

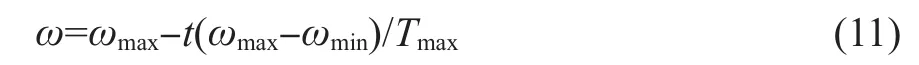
式中：Tmax——设定的最大迭代次数；ωmax——最大惯性权重；ωmin——最小惯性权重。

3.2.2 对约束条件进行处理

为了满足上述不等式条件约束，判断电动汽车充放电功率是否处于约束条件范围之内，如果超出约束条件的边界，需要根据式(12)和式(13)进行修正，使其满足设定的边界条件：

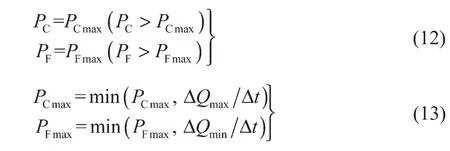
式中：Δt——单位时间。

采用罚函数的处理方法，将罚函数放入目标函数里，变换后的目标函数F′为

式中：F——原目标函数；K——惩罚系数；U——新增的罚函数；PLt——没有电动汽车时t时段电网的负荷。

3.3 算例分析与仿真

以潍坊青州王母宫地区为例进行算例分析，首先预测未来一天24 h电力负荷（表3），通过电动汽车集群方式进行削峰填谷平抑负荷波动，并在不同用户参与度下进行仿真分析。

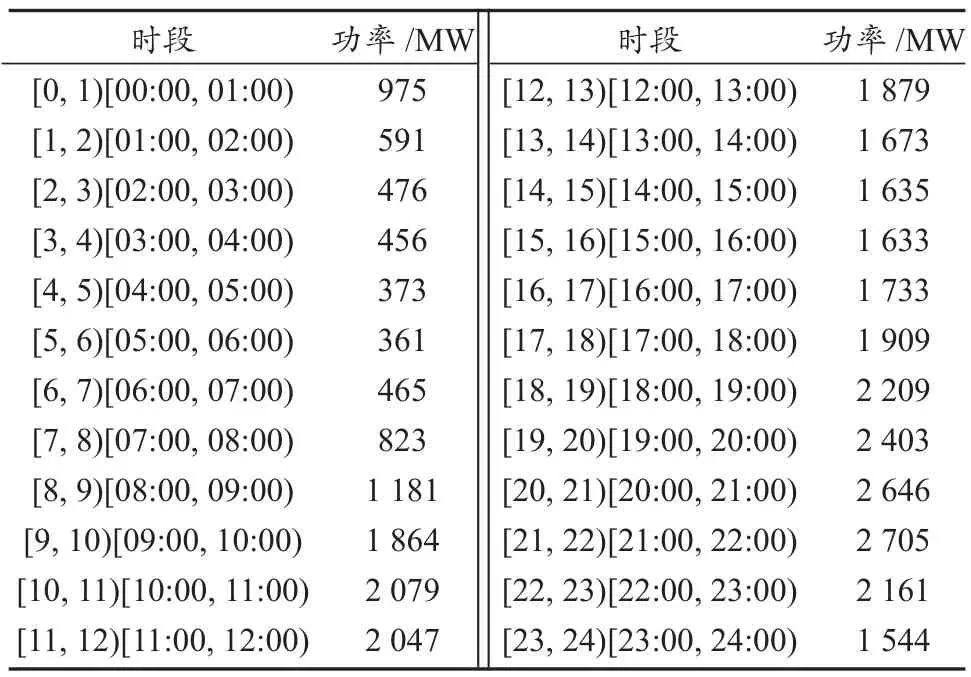
表3 电力负荷预测值Tab. 3 Power load forecasting values

将电动汽车集群，采用基于改进型粒子群算法对电网进行削峰填谷，并运用Matlab软件进行仿真。其中优化算法中参数设置如表4所示。

表4 粒子群算法参数设置Tab. 4 Parameters of particle swarm optimization algorithm

在用户参与度分别为20%、50%以及80%情况下，采用粒子群算法优化前后负荷曲线以及最优个体适应度曲线分别如图8和图9所示。可以看出，用户参与度越高，调峰效果越明显。因此，希望尽可能调动用户积极性，使之参与到削峰填谷这项服务中，这样不仅在更大程度上可缓解电网压力，而且用户通过充放电亦可获得差价收益。

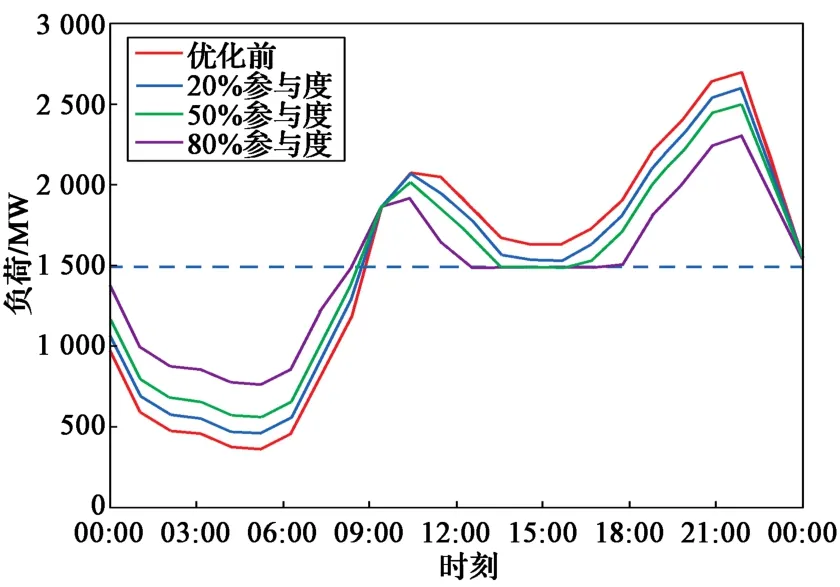
图8 削峰填谷优化前后负荷曲线Fig. 8 Load curves before and after optimization of peak showing and valley filling

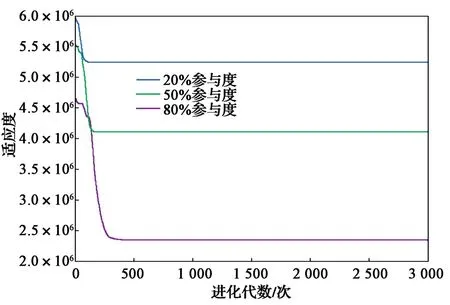
图9 最优个体适应度曲线Fig. 9 Optimal individual fitness curves

4 结语

本文首先针对区域电网进行电力负荷预测，相比指数平滑预测法，多层感知器神经网络能较准确预测未来电力负荷，为后续集群削峰填谷打下基础；其次，通过随机生成电动汽车参数并根据人为规则对电动汽车进行集群分类，再运用卷积神经网络进行训练，能有效将电动汽车集群；最后建立了电动汽车参与电网削峰填谷模型，考虑到不同用户参与度，采用改进型粒子群优化算法对其进行求解，仿真结果表明，电动汽车用户参与度越高，对缓解电网负荷波动越有利。

本文所提调度策略将所有参与削峰填谷的电动汽车可用容量均用来降低峰谷差，但并未考虑实际充放电时间、电池损耗等因素。除此之外，如何将参与调峰的容量合理分配到各电动汽车将作为下一步研究的内容。