一种重载列车自动驾驶操纵曲线规划方法
钟谱华,张征方,熊佳远
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
重载列车不仅吨位大、运行环境恶劣、相较于其他种类列车更难被操纵,而且对安全性和平稳性的要求更高,是列车自动驾驶应用场景中的重点和难点。列车操纵曲线是列车自动驾驶系统的核心功能,也是列车自动驾驶系统智能评价的重要参考依据之一。其主要包含未来一定区段内列车运行的位置、速度及牵引力/制动力等信息,规划了列车未来一定时间内的运动趋势。操纵曲线的合理性一定程度上决定了列车的运行品质,重载列车自动驾驶运行过程中遇到的速度控制和冲动等问题都可以通过调节操纵曲线得到一定程度的缓解甚至解决。因此,设计合理的操控曲线对重载列车自动驾驶系统而言至关重要。
自动驾驶操纵曲线是否合理,主要从安全性、平稳性、节能性和运行效率4方面进行评价。其中,安全性主要体现在列车运行过程中不超过列车自动保护系统(automatic train protection, ATP)限速、不冒进;平稳性主要体现在列车速度和牵引力/制动力变化平缓,运行过程中无冲动、涌动和晃动等现象发生;节能性主要体现在列车在单趟运行过程中能耗情况,耗能越少,节能性越好;运行效率主要体现在列车单趟运行过程耗时情况,单趟耗时越少,运行效率越高。
针对列车自动驾驶操纵曲线规划,文献[1]提出了一种基于神经网络模型的实时速度曲线规划算法来优化列车操纵指导,仿真表明利用该算法所得的速度曲线与基于二次规划的离线全局规划算法的速度曲线相吻合,且相比于优秀司机的操纵结果节能5.98%。文献[2]针对传统混合A*算法搜索效率较低且搜索路径平滑性较差的问题,文章提出一种基于等步长分层拓展的混合A*路径规划方法,可应用于非结构化道路场景,为智能车辆规划一条安全、平滑且满足车辆运动学约束的可行驶路径。文献[3]比较了蚁群算法、遗传算法和动态规划在求解特定线路最优操纵曲线问题的应用,研究发现蚁群算法在稳定性和效率方面平衡性更好。文献[4-5]研究了遗传算法在列车目标速度曲线规划中的应用,试验结果表明基于遗传算法的目标速度曲线满足列车运行的安全性、准点性和节能性等需求。文献[6]研究了求解列车准点节能运行最优控制问题的间接法,提出了一种列车运行控制工况最优切换点的求解方法,通过仿真求解了最优控制工况序列、最优速度和工况转换的时机。文献[7]提出了一种基于行程预规划的机车节能操纵优化控制算法,其基于线路数据和机车参数来预规划机车运行状态,并基于实时状态进行调整,在半实物仿真测试平台上测试,测试结果相比人工操纵列车的运行数据,平均节能约11.47%。文献[8]提出了一种基于两列以上高速列车运行模型的节能曲线规划方法,其利用武广高铁的线路数据,将该方法规划的操纵曲线与司机实际运行的操纵曲线进行比较,验证了该方法的节能效果。文献[9-10]提出了一种针对移动闭塞信号系统的列车运行曲线规划方法,其将列车轨迹规划问题转换为线性时不变系统的求解问题,并通过仿真验证了该算法的效果。文献[11]提出了一种基于启发式动态规划的列车运行速度曲线优化方法,并基于北京地铁亦庄线线路条件进行了仿真,验证了该算法的节能效果。文献[12]建立了考虑势能因素的列车节能模型,设计了基于该模型的节能曲线规划方法,其可为城轨和地铁线路规划和设计提供参考。文献[13]建立了详细的列车动力学模型并设计了列车运行的多目标优化指标,通过迭代求解的方式得到了列车目标速度运行曲线。文献[14-15]研究了重载列车的操纵优化,通过仿真验证了在满足列车安全性和准点要求的条件下规划的操纵曲线能兼顾操纵平稳性和节能性。文献[16]研究了地铁运行过程中的节能问题,考虑运行过程中的多车交互因素和准点要求,提出了一种速度轨迹优化控制策略,通过在北京地铁7号线的试验验证了该控制策略的有效性,采用该策略能降低16.24%的能耗。文献[17]研究了地铁运行过程中的节能问题,建立了地铁运行的多质点模型,考虑实时变化的乘客流,提出了一种新的基于改进差分进化算法的速度轨迹优化控制策略,通过南宁地铁1号线的应用情况验证了基于该方法规划的速度轨迹比基于传统差分算法规划的速度轨迹具有更好的节能效果。文献[18]研究了列车在给定时刻表条件下的到点/开点时刻调度和速度轨迹规划,其以节能为目标,研究了单车和多车的规划问题,并将该算法用于荷兰铁路单轨和双轨试验,结果验证了采用该算法在给定时刻表下可提升能量利用效率。文献[19]研究了部分系统参数不确定条件下的列车速度轨迹规划问题,包括牵引力和阻力的不确定性等,建立了该问题的马尔可夫决策过程模型,提出了一种新的数值求解方法和一种新的速度轨迹规划策略,通过基于实际运行数据的仿真,验证了该策略的节能效果。文献[20]研究了中速磁浮列车的节能问题,提出了一种通过动态规划实现速度轨迹规划的方法,仿真结果表明采用该方法能确保中速磁浮系统安全运行和实现节能。
在以上提出的规划方法中,大部分方法对实际运行中的安全性因素考虑不足,未涉及牵引力变化率、制动力变化率等约束,规划的速度曲线中存在牵引力/制动力变化过快的情况,在实际应用过程中可能造成列车冲动;部分方法考虑的性能相对单一,缺乏择优的过程,过于关注一种性能可能导致规划方法在其他性能上表现欠佳,影响算法的整体效果。为此,本文提出一种重载列车运行曲线规划方法。其在第一条操纵曲线规划过程中,生成基于ATP的简单诱导曲线;在合理范围内随机生成步长,引导列车运行状态向诱导曲线上的运行状态转移,完成单条操纵曲线的生成;通过设计性能指标,在规划的多条操纵曲线中择优,选取总指标最优的操纵曲线,迭代更新作为下一次的诱导曲线或输出作为最终的操纵曲线。
1 车辆模型、约束及评价指标
车辆模型是重载列车自动驾驶操纵曲线规划的基础。在规划操纵曲线时,操纵曲线需满足一定的约束条件以更符合实际情况下的运行状况;同时,需要考虑设计评价指标以评价操纵曲线的优劣。文中位置变量单位均为m,速度变量单位均为km/h,牵引力/电制力变量单位均为kN,质量变量单位均为t,时间变量单位均为s。
1.1 车辆模型
重载列车车身长、结构复杂。在纵向动力学研究范围内,重载列车车辆模型被简化为一个多质点的质量弹簧阻尼系统[13]。

图1 列车多质点模型Fig. 1 Train multi-particle model
对第i节车,其动力学模型如下:

式中:xi——第i节车的位移;——第i节车的惯性力;Fi,G——第i对车钩的车钩力,,K为车钩的劲度系数,C为车钩的阻尼系数;Fi,B——第i节车所受的空气制动力;Fi——第i节车的牵引力或制动力;Fi,C——第i节车所受的基本阻力;Fi,R——第i节车所受的弯道阻力;Fi,W——第i节车所受的坡道阻力;n——车辆数。
1.2 列车运行约束
列车运行约束体现了机车性能、操纵要求等因素对自动驾驶系统的影响,本文考虑的列车运行约束主要包括机车能力约束、安全性约束及平稳性约束等。
机车能力约束主要用机车的牵引/制动特性曲线表示。该约束表征重载列车在特定速度下的最大牵引力和电制动力输出能力:

式中:Fi,T——最大输出牵引力;Fi,E——最大输出制动力;vi——重载列车速度。
列车运行过程中,需确保列车的目标速度曲线低于LKJ所设定的ATP速度vi,LKJ,见式(4),否则可能出现超速和冒进的风险。

为保证列车运行过程的平稳性,需确保机车输出的牵引力/制动力平缓变化。设定牵引力/制动力变化所允许的最大上升斜率gi,up和最大下降斜率gi,down,将Δt时间内机车输出的牵引力/制动力Fi的变化范围限制在[Fi,min,Fi,max]:

1.3 评价指标
针对本文提出的操纵规划方法,下面将从安全性、平稳性、能耗和运行效率的角度设计指标,以评价所规划的操纵曲线是否合理。
(1) 安全性指标J1
从列车运行的安全性考虑,运行过程中若出现超速现象,则该操纵曲线被认为不合理。因此,一旦发现规划的操纵曲线存在超速点,则安全性指标为1,其余情况安全性指标为0。

(2)平稳性指标J2
列车平稳性主要考虑列车运行过程中的牵引力/制动力变化情况,若牵引力/制动力剧烈变化,在重载条件下,极有可能造成列车冲动和涌动。平稳性指标J2主要考虑运行过程中的牵引力/制动力变化情况。该指标越小,表征列车加速度变化越平缓,手柄级位保持越好,运行相对越平稳[14]。智能驾驶系统将规划的操作曲线离散为M段,令第l段所规划的牵引力/电制力为Fl,该段规划的牵引力/电制力变化量为ΔFl=Fl-F(l-1),且ΔF1=0,则有

(3)能耗指标J3
能耗指标评价列车运行过程中的能耗情况,能耗指标主要是牵引力/制动力的做功情况。该指标越小,表征自动驾驶运行过程越节能[15]。智能驾驶系统将规划曲线离散为M段,令第l段所规划的距离为Sl,不考虑硬件层面问题、摩擦损耗等因素,不考虑弯道阻力、坡道阻力等在相同位置近似为定值的阻力所消耗的电能,按照第l段规划曲线运行的能耗指标可以近似为牵引力/制动力所做的功|FlSl|,则每段规划曲线的能耗指标之和为总能耗指标。

(4)运行效率指标J4
运行效率指标主要根据机务段提升运量的目标进行设置。考虑以通过特定区段的运行时间作为运行效率指标,从起始点到终点的时间越短,运行效率越高;所需时间越短,该区段内列车运行平均速度越高,列车运行效率越高。
智能驾驶系统将规划的操纵曲线离散为M段,令第l段操纵曲线初速度为vl,末速度为v(l+1),故运行第l段规划距离的运行时间为,M段规划曲线的运行时间之和为总运行效率指标。

(5 )总指标J
由于各指标所考虑参数的绝对数值不同且不同条件下对特定性能可能有侧重,因此对各指标设置权重并将其作为系数加入各指标中,以防止因某一指标在数值上过于突出而造成求解过程陷入局部最优情况的发生。
综上,总指标J被设置为

式中:k1——安全性指标的权重;k2——平稳性指标的权重;k3——能耗指标的权重;k4——运行效率指标的权重。
在本文算法,一旦有超速情况,即认为该操纵曲线不合理,故设置k1为无穷大;在确保无超速的情况下,主要考虑平稳性指标、能耗指标和运行效率指标。
2 算法实现
本文所提重载列车自动驾驶操纵曲线规划方法在单次迭代周期内,通过设置随机探测步长和跟随诱导曲线的方式,生成多条操纵曲线进行择优,选择使总指标达到最优的操纵曲线进行输出,并作为下次迭代过程的诱导曲线。最优操纵曲线的规划过程如图2所示。

图2 最优操纵曲线的规划过程Fig. 2 Planning process of the optimal manipulating curve
2.1 诱导曲线更新
规划的核心任务是在已知位置和速度的前提下选择合适的牵引力/制动力。作为一种启发式的规划方法,规划操纵曲线中每一点所选择的牵引力/制动力大小信息都来自诱导曲线。诱导曲线既要包含一定的位置和速度信息,又不能包含过多的先验经验,以避免算法具有特殊性。在已知ATP限速的基础上选择第一条操纵曲线,其为将ATP限速减5得到的曲线。在完成一轮迭代后,所得到的性能指标最优的操纵曲线被作为新的诱导曲线进行下一轮迭代。
2.2 随机探测步长
诱导曲线表征该区段内所期望的列车理想运行状态。但实际应用过程中,受列车特性和操纵约束的限制,列车只能向诱导曲线逼近,无法完全实现参照诱导曲线运行。在列车当前位置,考虑获取前方一定长度范围内(而不是所有)的诱导曲线信息,该长度范围即为探测步长,将其设定为Sstep,单位为m。事先无法得知Sstep的最佳取值,考虑为其设置上界Sstepmax和下界Sstepmin,在该范围内随机生成Sstep。设置Sstepmax是为了防止所选取的步长太长,对临时限速、列车阻力等信息考虑不足;设置Sstepmin是为了防止选取的步长太短,导致单条操纵曲线生成过程中运行次数过多,影响算法的运行效率。Sstep的生成公式如式(12)所示。
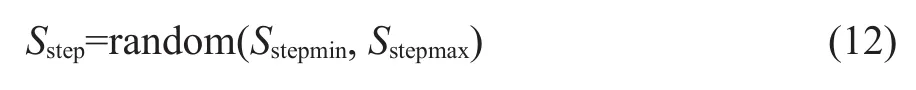
2.3 计算工况级位
操纵曲线上每一点都包含位置、速度、牵引力/制动力这3种信息,设机车当前状态速度为vi,位置为Si,牵引力/制动力为Fi。
将Sstep范围内诱导曲线等距离离散为N个点,其中第j个点的位置为Si,j,速度为vi,j,牵引力/制动力为Fi,j,则从当前状态位置到诱导曲线上第j个点的位置差值为ΔSi,j,从当前状态速度到诱导曲线上第j个点的速度差值为Δvi,j,具体如下:

当前状态位置到诱导曲线上N个点的位置差值最大值为ΔSi,max,从当前状态速度到诱导曲线上N个点的速度差值最大值为Δvi,max,从当前状态牵引力/制动力到诱导曲线上N个点的牵引力/制动力差值最大值为 ΔFi,max。

列车当前状态(Si,vi,Fi)、诱导曲线的示意如图3所示。

图3 当前状态和诱导曲线的示意图Fig. 3 Schematic diagram of current state and induction curve
设当前状态与诱导曲线第j个点连直线,沿该直线运行的加速度为ai,j,所需牵引力/制动力为Fj,a,则有

式中:P——机车质量;G——货车质量;γ——旋转质量系数。
权重系数wi,j用于表征当前状态与诱导曲线上第j个点状态差异的大小。状态差异越大,表征相同的机车能力条件下当前状态应尽快向诱导曲线上第j点状态转移,第j点状态在诱导曲线的N个点中对当前状态吸引的权重越大。相反,当前状态越接近第j点状态,表征当前状态无须做出太多调整即可到达第j点状态,第j点状态在诱导曲线的N个点中对当前状态吸引的权重越小。

当前状态所选择的牵引力/制动力为

实际机车输出的牵引力/制动力应满足机车能力、安全性和平稳性约束,即牵引力/制动力输出不能超过机车的最大能力限制,牵引力/制动力变化斜率必须满足平稳性要求。令机车能力和平稳性约束分别为fi,TE(F)和fi,g(F),施加约束后最终得到的下一点状态的牵引力/制动力为

2.4 机车状态转移
在已知到达下一点状态的牵引力/制动力F(i+1)后,可以计算下一点状态的位置和速度。设定规划过程两个相邻点之间的时间步长为tf,令两个相邻点之间的距离为di,di与当前状态速度Vi和设定的时间步长tf相关,见式(24)。确定F(i+1)后,下一点状态位置为Si+di,见式(25),下一点状态下位置和速度如下:
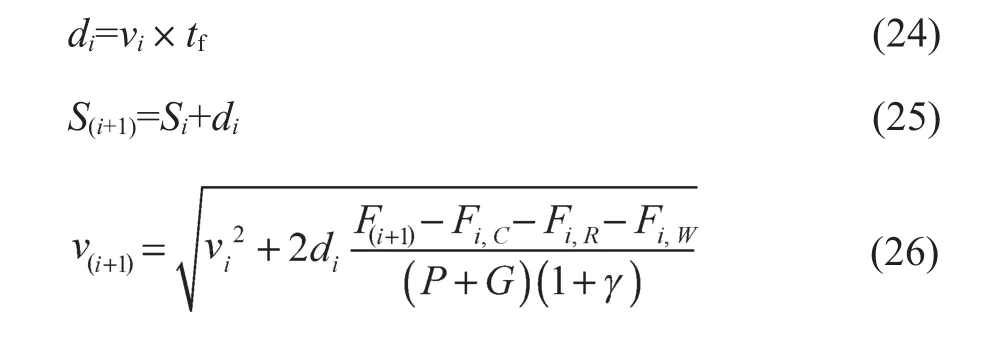
式中:S(i+1)——下一点状态下位置;v(i+1)——下一点状态下速度。
2.5 计算性能指标
得到下一点状态下S(i+1)和v(i+1)后,完成由当前状态向下一点状态的转移。从初始位置S0、初始速度v0、初始牵引力/制动力F0出发,依次规划M个点,得到一条完整的操纵曲线Lk,计算该操纵曲线的总指标:

2.6 择优操纵曲线
通过之前的步骤,从初始状态(S0,v0,F0)出发,依次规划每个点的牵引力/制动力,计算每个点的位置和速度,得到整条操纵曲线Lk,并计算了Lk的总指标Jk。重复从初始状态(S0,v0,F0)规划得到整条操纵曲线的过程,由于探测步长Sstep在一定范围内随机,得到的每条操纵曲线存在区别。
在本轮迭代周期得到的所有规划曲线中,选择综合性能指标J最小的操纵曲线Lk。
2.7 输出操纵曲线
将该操纵曲线L作为下一轮迭代过程的诱导曲线,进行下一轮迭代过程。当迭代达到一定次数或综合性能指标小于设定的数值时,结束迭代,输出操纵曲线。
3 仿真结果
采用神朔铁路的神木北站至黄羊城站区段线路数据进行仿真。该区段大上坡较多,最大的上坡坡度为12‰,列车通过时需要较大的牵引力;弯道方向多变且半径相对较小,列车通过时弯道阻力变化频繁,在重载、大牵引力的条件下容易发生列车冲动和涌动,严重影响列车运行的平稳性。规划合理的操纵曲线,是重载列车自动驾驶亟待实现的一个功能,依此可降低此区段内列车运行的牵引力/制动力变化率,进而避免冲动和涌动的产生。
仿真采用神木铁路现场常见的万吨“3+0”编组列车参数,表1示出部分仿真参数。
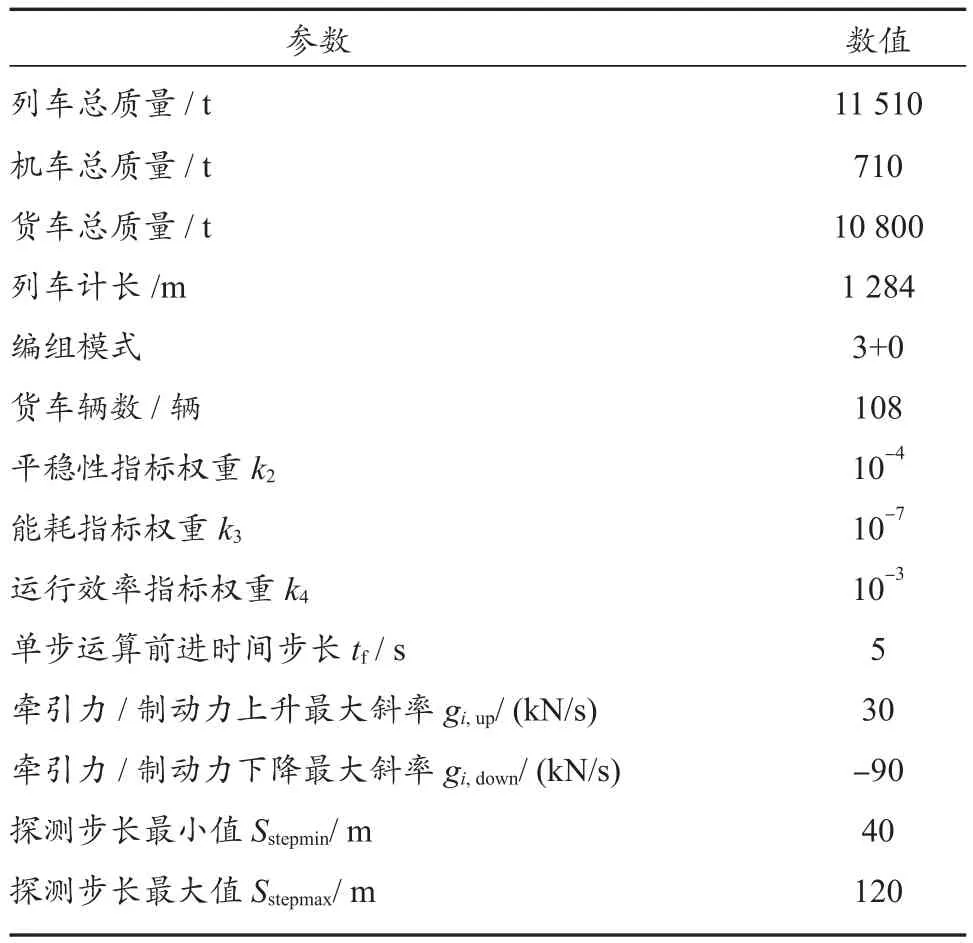
表1 仿真参数表Tab. 1 Simulation parameter
图4示出第1次、第3次和第8次迭代更新后输出的规划操纵曲线。可以看出,随着迭代次数的增加,总体而言,规划的操纵曲线越来越光滑,表征列车运行过程中牵引力/制动力的变化更加平缓,列车操纵平稳性更好。从局部细节来看,在ATP限速变化的区域,迭代次数较少时,规划的操纵曲线存在类似“超调”的情况,表征为曲线前半段下降过多而后半段重新拉升,存在较明显的转折点(实际运行过程中在转折点处容易产生冲动,影响列车的平稳性)。在第8次迭代的操纵曲线中,在ATP限速变化的区域操纵曲线的“超调”基本消失,操纵曲线平缓过渡,这表征列车操纵平稳性有较大提升。可见,随着迭代次数的增加,8次迭代后,操纵曲线得到较大改善,已趋于收敛。

图4 第1次、第3次和第8次迭代输出的操纵曲线Fig. 4 Manipulation curves of the first, third and eighth iterations
图5~图8分别示出随着迭代次数增加而变化的总指标、平稳性指标、能耗指标和运行效率指标。8次迭代输出曲线的具体指标数值如表2所示。结合图表进行分析,从第1次进行到第8次迭代过程中,操纵曲线的4个指标数值上都有减小,随着迭代次数增加,斜率越来越小,经过8次迭代后输出曲线已趋于稳定。总指标从初次迭代结果的4.702 5减小至第8次迭代结果的3.856 3,相较于最初的操纵曲线减小了17.99%;平稳性指标从1.581 5减小至0.860 3,相较于最初的操纵曲线减小了45.60%;能耗指标从1.744 5减小至1.709 0,相较于最初的操纵曲线减小了2.03%;运行效率指标从1.376 5减小至1.287 1,相较于最初的操纵曲线减小了6.49%。分析各指标情况,随着迭代次数的增加,列车的平稳性提升明显,而能耗和运行效率有小幅提升。

图5 迭代过程中的总指标Fig. 5 Total indices in the period of iteration

图6 迭代过程中的平稳性指标Fig. 6 Stability indices in the period of iteration

图7 迭代过程中的能耗指标Fig. 7 Energy consumption indices in the period of iteration

图8 迭代过程中的运行效率指标Fig. 8 Operation efficiency indices of in the period of iteration
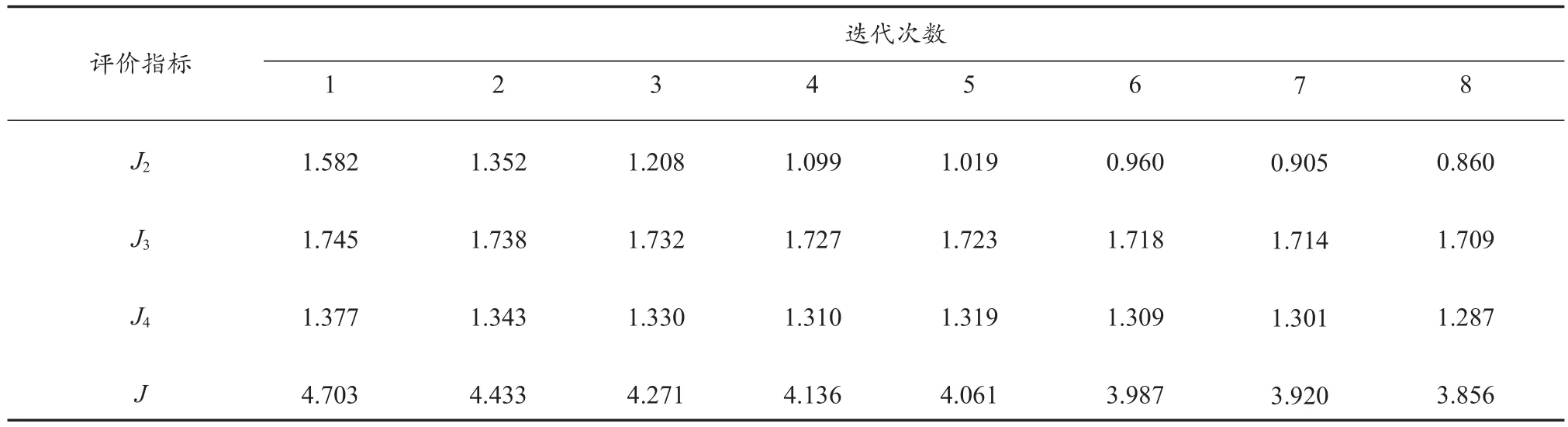
表2 8次迭代所输出操纵曲线的指标数值Tab. 2 Each index of manipulating curves by eight iterations
进一步分析各指标减小的结果及迭代过程,第1次迭代的诱导曲线为ATP限速减5,该诱导曲线代表着该区段所有操纵方法中运行效率最优的“可望而不可及”的运行状态,以该曲线为诱导曲线所规划的操纵曲线运行效率都相对较高,导致后续迭代过程中操纵曲线的运行效率指标提升较小。同理,第1条诱导曲线中存在大量恒速过程,相当于机车整个过程的能耗仅包含各阻力能量消耗及ATP限速下降时的制动能量消耗,一定程度上表征列车运行过程中的理想能耗状态,以此曲线为诱导所得到的操纵曲线能耗也相对较好。与能耗和运行效率相反,第1条诱导曲线基本未考虑列车操纵平稳性等问题,存在明显的“速度转折点”,平稳性相对较差,列车操纵平稳性的提升空间相对较大,在此基础上,后续的迭代过程不断地改善列车运行的操纵平稳性,使该性能有明显的提升。通过跟随能耗指标、运行效率指标较优的诱导曲线,不断迭代更新,生成能耗指标和运行效率指标小幅提升、操纵平稳性指标大幅提升的操纵曲线,从单目标最优的诱导曲线出发,最终实现了多目标的优化效果。
4 结语
本文提出了一种基于启发式诱导曲线和择优的重载列车自动驾驶操纵曲线规划方法,其通过跟随启发式诱导曲线和生成多条曲线择优的方式,迭代更新诱导曲线并输出择优的操纵曲线。仿真结果表明,在第1次迭代中,规划方法已生成一条可行的操纵曲线;随着诱导曲线的迭代更新,8次迭代后,操纵曲线的平稳性指标相较于第1次生成的操纵曲线降低了45.60%,能耗指标相较于第1次生成的操纵曲线降低了2.03%,运行效率指标相较于第1次生成的操纵曲线降低了6.49%,总指标相较于第1次生成的操纵曲线降低了17.99%,列车的操纵平稳性、节能性和运行效率都有提高,其中平稳性提升较大。
本文所提出的自动驾驶操纵曲线规划方法中,探测步长和单步运算前进时间步长的选取对所生成的操纵曲线影响较大。诱导曲线的探测步长与线路条件等因素相关度较高,在随机步长的选取上,可采取自适应性更强的方法;单步运算前进时间步长表征状态转移的频率,时间越短,状态转移越频繁,获得的曲线可能越光滑,但计算量也可能迅速增大,影响算法的实用性。因此,如何智能、自适应地选取步长是提高该算法性能的关键,是我们下一步的研究方向。

