基于混合整数线性规划的城市轨道交通列车
一体化节能运行曲线优化研究
张 瞄,张朝阳,胡云卿,卿光明,张 宇
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
城市轨道交通以其准点、便捷、安全、绿色的特点成为城市交通运输的重要方式之一,其承担着城市较重的运输压力。尤其是在经济发达、人口众多的大都市,城市轨道交通发展较早且目前多呈网络状分布。在此形势下,城市轨道交通系统能耗逐年递增。在系统能耗中,列车牵引能耗约占总能耗的50%[1-2],因此降低牵引能耗成为提高能量利用率的重要途径,也成为运营商和学者们开展研究的热点问题之一。
对于轨道交通领域的节能问题,国内外诸多学者针对单站间给定运行时分下的节能优化驾驶策略展开了研究,部分学者首先基于庞特里亚金极大值原理[3]探讨了列车节能运行的4种工况,即最大牵引、巡航、惰行和最大制动。在此基础上,学者们根据列车动力学的单质点模型,采用了不同的算法来搜索最佳工况序列。文献[4-6]分别采用遗传算法在给定惰行点数量条件下求解最佳工况序列,或连续或基于时域离散或基于S域离散,一般设定每个站间的惰行点不超过2个。在这类给定惰行点数量的研究基础上,文献[7]进一步拓展了研究,采用动态变化的染色体长度表示变化的惰行点数量,依此来搜索最佳惰行点,从而获取最佳工况序列,这种考虑更贴近实际应用场景。此外,部分学者探索了其他不同算法,如蚁群算法[8]、动态规划算法[9]、迭代算法[10]和数值算法[11]等,这些算法都被广泛应用到最佳工况序列的节能运行曲线规划研究中。
实现列车牵引节能的另一个研究方向是列车站间冗余时分的分配策略。冗余时分的调整实际上是对线路站间运行时间进行了调整,因此这一类研究问题其实属于列车运行图调整问题范畴。站间冗余时分被定义为列车实际运行时分与最短运行时分的差[12]。站间冗余时分的引入一方面是为了增强列车运行图的鲁棒性,在发生一定程度的小干扰时,列车可快速恢复至计划列车运行图状态;另一方面,通过合理利用站间冗余时分,可以降低能耗。对于同一站间,分配的冗余时分越多,降低的能耗值越大。因此不同的冗余时分分配策略会造成不同的节能效果,部分学者就此开展了相关研究。文献[13]针对城市轨道交通列车一体化优化问题提出了一种迭代双层优化模型,其第一层决定牵引、惰行和制动这3种工况的转换点,第二层则优化冗余时间分配策略,遗传算法也应用在其模型中进行求解。文献[14]也同样考虑到城市轨道交通列车运行图与速度曲线一体化优化问题,建立了双层规划模型,并提出了一种数值算法进行合理求解。
本文针对城市轨道交通列车节能运行曲线规划问题,综合考虑了列车牵引特性以及限速坡度等线路条件,建立了列车冗余时分分配与定时节能驾驶策略一体化优化模型(一体化是指针对单条线路构建列车运行时分和速度曲线一体化优化模型)。该模型采用混合整数线性规划(mixed integer linear programming,MILP)框架,并通过Matlab调用商业软件CPLEX进行快速求解。
1 城市轨道交通列车一体化节能运行曲线优化模型
对于不同站间,能耗与运行时分的函数关系不同,因此将相同的冗余时分分配至不同站间可以得到不同的节能效果。图1示出站间冗余时分分配策略实现节能的原理。两条曲线表示两个站间(红色线表示站间1,蓝色线表示站间2)的能耗与运行时分关系,即使分配相同的冗余时分ΔT,二者可以减少的能耗量也不同;在冗余时分分配过程中,应尽可能把时间分配给节能效果好的站间。

图1 冗余时分分配节能原理示意Fig. 1 Schematic diagram of reserved time distribution principle
1.1 列车动力学模型
由于线路条件(如限速、坡道等静态信息)是基于位置给定的,因此考虑空间特性的城市轨道交通列车的运行过程可采用经典单质点连续模型进行描述:

式中:m——列车质量;ρ——旋转质量因子,一般取1.06;E——单位质量动能,E=0.5v2;v——列车速度;s——位置;u——控制变量,正值表示牵引力,负值表示制动力;R——基本阻力,与速度相关;G——附加阻力,本文仅考虑坡道阻力,故G与位置相关,表示为s的函数;t——时间。
由文献[15]可知,单位基本阻力可表示为速度的二次函数。相较于牵引力和制动力,基本阻力数值较小,因此也可忽略速度的一次项部分,仅考虑常数项和二次项,将基本阻力转换为与E相关的线性函数:

式中:g——重力加速度;a1——常数;a2——与速度相关的二次项系数。
坡道阻力G可用式(3)进行计算:

式中:α——坡度千分数,正值代表上坡,负值代表下坡。
1.2 一体化节能运行曲线优化模型
本文所考虑的城市轨道交通线路如图2所示,其以降低牵引能耗为优化目标,建立考虑冗余时分分配及单站间定时节能的一体化优化模型。

图2 城市轨道交通线路布局图Fig. 2 Layout of urban rail transit line
该一体化优化模型为双层框架,上层对站间冗余时分进行分配,获取最佳节能冗余时分分配策略;下层基于上层站间冗余时分分配方案给定的站间运行时间优化列车站间运行速度曲线,具体框架如图3所示。

图3 优化模型双层框架Fig. 3 Double-level framework of the optimal model
模型中,目标函数线路上的总牵引能耗J为各站间牵引能耗Ji之和。在不考虑再生制动能的条件下,牵引能耗可通过牵引力对位置积分计算,具体计算公式如下:
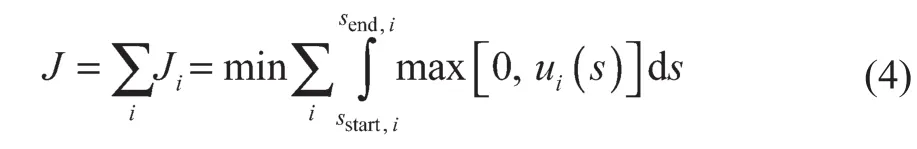
式中:i——站间索引,i∈{1, 2, …,I};I——站间总数,即线路有I+1个站;sstart,i——第i个站间的起点;send,i——第i个站间的终点;ui(s)——第i个站间的控制变量。
为保证列车准点、安全运行,模型除了需满足列车动力学约束条件即式(1)外,还需满足线路限速、列车牵引特性以及边界约束条件,具体如下:

式中:E(sstart,i)——列车在第i个站间的起点动能;Estart,i——列车在第i个站间的动能初始值;E(send,i)——列车在第i个站间的终点动能;Eend,i——列车在第i个站间的动能末值;Ti——列车在第i个站间的运行时间;Emax,i——列车在第i个站间的最大动能;Ei(s)——列车在第i个站间的动能;umax——根据电机特性获取的最大牵引/制动力;umin——根据电机特性获取的最小牵引/制动力。
约束条件式(1)~式(8)为下层模型。约束条件式(5)表示列车在第i个站间的起点和终点动能应为动能的初始值和末值,其中动能的初始值vstart,i为列车在第i个站间的起始速度,即为0。同理可得动能末值,vend,i为列车在第i个站间的末速度,也为0。由于式(1)中动能E位于分母位置,无法为0,因此本文设定动能初始值和末尾值均为0.1J。约束条件式(6)表示列车在第i个站间的运行时间为Ti。约束条件式(7)表示列车在第i个站间的动能均不能超过Emax,i,限制列车实际运行速度不能超过限速,。约束条件式(8)限制了列车实际控制量,牵引力不能超过根据电机特性获取的最大牵引力,提供的制动力也不能超过最大制动力。
约束条件式(9)是上层模型,其为冗余时间分配约束条件条件。考虑到准点以及车辆衔接的需求,约束条件式(9)限制了列车总运行时间,并使其保持不变;各站间运行时间通过冗余时间的分配,可以在一定范围内变化。
由此构建了一体化优化模型,其既保证了线路总运行时间不变,同时在各站运行时间为Ti的条件下,又能满足列车动力学模型约束条件以及边界约束条件。由于连续空间的此类无限维度的优化问题很难被求解,因此需对模型进行离散化处理。即对每个站间基于S域进行分段处理,每一个小区段内的线路坡度值和限速值均为常数,并假设牵引/制动力也保持不变。将第i个站间分为Ni段,每段间隔长度Δsn,i,以n作为分段索引,离散后的优化目标如下:
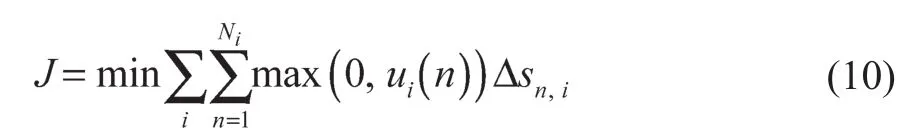
离散后的优化模型不仅仍需满足线路限速、列车牵引特性以及边界约束条件,见式(5)~式(9),同时还需满足根据列车动力学模型离散后获取的动态方程约束条件:

式中:Ei(n)和ui(n)——简写的E(sn,i)和u(sn,i),其中E(sn,i)表示第i个站间第n段的动能,u(sn,i)表示第i个站间第n段的控制变量;an,i,bn,i,cn,i——可求的系数。
状态变量E的动态方程可通过微分方程求解用式(11)进行表达[16];式(12)则可由式(1)中状态变量时间t的微分方程结合梯形积分公式获得。为实现an,i、bn,i和cn,i这3个系数的简单计算,本文采取了与文献[16]不一样且更为简单的计算公式来获取这3个系数的值,从而避免了复杂的指数计算。根据运动学公式可得
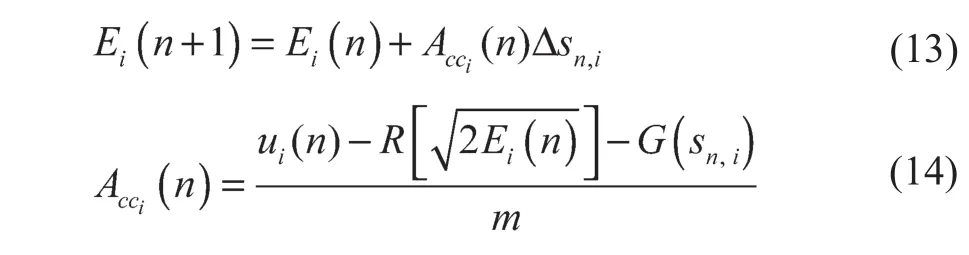
联立式(11),式(13)及式(14),可得

由此,本文已构建了考虑冗余时间分配和单站间定时节能的列车运行曲线一体化优化模型。该模型为一个混合整数非线性规划模型,其中仍存在诸多非线性项。
2 MILP模型求解算法
针对第1.2节所建立的混合整数非线性规划模型,本文考虑采用Piese-Wise-Affine(PWA)函数以及不同的线性化法则对所提列车运行曲线一体化优化模型中的非线性项进行线性化近似或等效,将模型转换为混合整数线性规划模型进行求解。
2.1 非线性函数线性化
由于在时间动态方程中存在非线性函数项,本文借鉴文献[16]中的方法采用PWA函数进行分段线性近似:
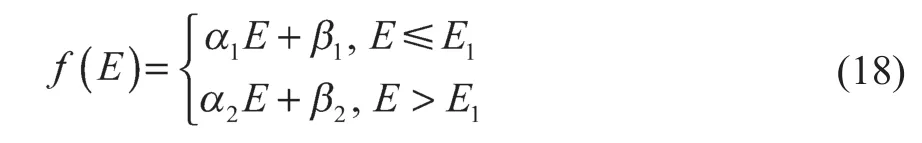
式中:α1,α2,β1,β2——分段后线性拟合系数;E1——特性曲线分段点。
引入逻辑变量δ1,令

则式(18)分段线性近似的f(E)被等效为
f(E)=δ1(α1E+β1)+(1-δ1)(α2E+β2) (20)同时还需引入式(21)所示约束条件来表示式(19)所示逻辑关系:

式中:ε——极小正值。
此外,式(8)约束条件中同样存在非线性函数项umax,电机牵引特性通常分为恒转矩、恒功率和自然特性区。同理,采用PWA函数对其进行线性近似,见式(22),其中E2和E3为特性曲线的两个拐点且E3>E2。
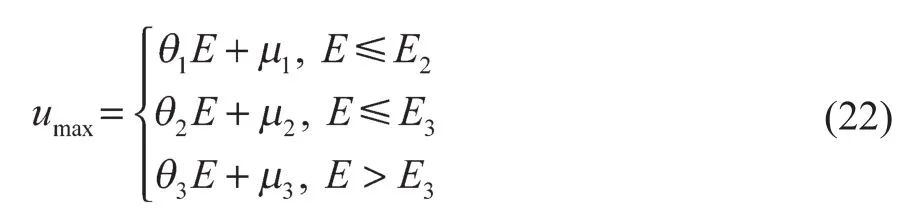
式中:θ1,θ2,θ3,μ1,μ2,μ3——分段后线性拟合系数。
引入逻辑变量δ2和δ3,令

则式(22)等效为

同理,需引入约束条件:

2.2 非线性乘积线性化


3 仿真案例
为验证所提数据设计了仿真案例,其基于采用Intel ® Xeon R Gold 6136 CPU@3.00GHz处理器和6GBRAM的计算机平台,通过Matlab调用CPLEX函数求解节能运行曲线优化问题。
3.1 仿真参数配置
以上行方向为例,长沙地铁4号线的线路如图4所示,4号线共有25个站点即24个站间,线路与列车的基本参数分别如表1和表2所示。图5展示了该线路不同站间的限速与坡度曲线。表3为非线性函数f(E)和umax分段线性近似的系数,二者均采用分两段近似方法。由于列车速度在0~21.11 m/s范围内,为提高近似精确度,减小近似误差,本文针对3段不同范围的速度进行分段近似。
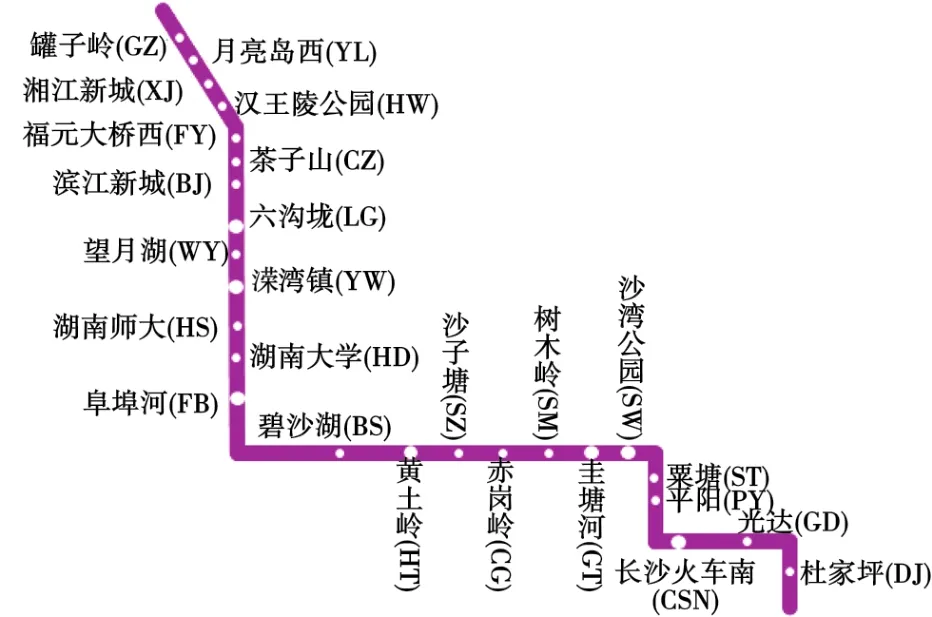
图4 长沙地铁4号线站点布局图Fig. 4 Layout of the Changsha subway No.4 line
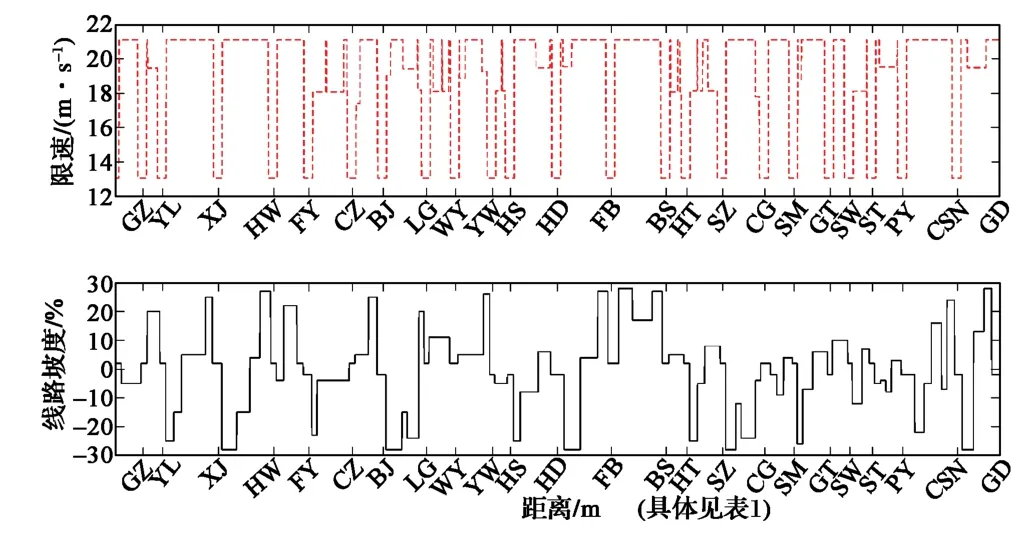
图5 长沙地铁4号线线路限速及坡道曲线Fig. 5 Speed limits and grade profiles of the Changsha subway No.4 line

表1 长沙地铁4号线基本参数Tab. 1 Parameters of the Changsha subway No.4 line

表2 列车基本参数表Tab. 2 Basic train parameters

表3 f (E)和umax 的PWA分段线性近似系数Tab. 3 Piece-wise-affine coefficients of f (E) and umax
在该仿真案例中,为了平衡计算精度与计算时间,将每个站间分为20段,每一段内限速和坡道值相同,控制变量也保持不变。
3.2 仿真结果分析
CPU计算时间为14.37 s,gap值为0.03%,求得的优化后的列车运行速度曲线如图6所示。这里,其中BP为整数连续后得到的最优解,BF为当前求解器求得的整数时的解。图6中,所有速度值均满足限速条件;惰行点在下坡点处时,通过下坡道提供的与基本阻力方向相反的附加阻力使得列车速度提升,以减少牵引能耗。优化后的各站间运行时间与牵引能耗如表4所示。由表可知,无论是相较于本公司现有ATO运行数据,还是计划运行时间,线路中站间运行时间都进行了调整,部分站间运行时间被缩短。例如茶子山站-滨江新城站(CB)线路,运行时间由121.3 s缩短至112.5 s。将该线路站间冗余时分分配至节能更多的站间,导致另一部分站间运行时间延长。例如阜埠河-碧沙湖(FB)线路,运行时间由133.2 s增加至139.7 s,但全线总运行时间与总计划运行时间2 475 s的偏差仅4.9 s,在允许偏差范围内。与现有控制结果相比较,优化后可以达到(421.2-351.9)/421.2=16.5%的节能效果,证明了该算法的有效性。

图6 全线速度曲线及牵引/制动力优化结果Fig. 6 Optimal results of speed profiles and tractive/braking forces

表4 能耗与站间运行时间优化结果Tab. 4 Optimal results of energy consumption and running time between inter-stations
为展示算法实现节能的细节,本文以上行方向第22个站间线路(平阳-长沙火车南站)为例,优化后的站间运行曲线如图7所示。在该站间线路,列车牵引至46 km/h左右后线路坡度转为负值,列车将牵引工况切换为惰行工况,利用下坡时正的坡道阻力克服空气阻力以保持车速,达到节能的目的。坡度由正转负时,仍然采用惰行工况降低车速,以避免不必要的制动;同时也减少了因力的切换而引起的列车颠簸,提高了乘客的舒适度。
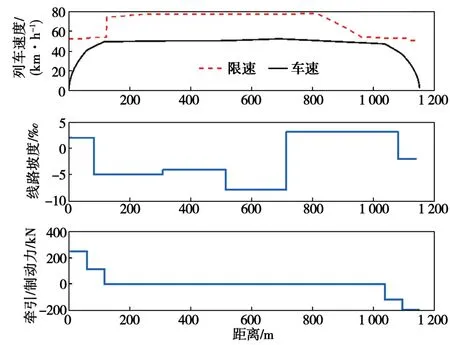
图7 平阳-长沙火车南站间优化运行曲线Fig. 7 Optimal train trajectory between Pingyang and south Changsha railway stations
3.3 平台验证分析
为了进一步验证该算法的有效性,在Matlab仿真结果基础上结合路网车一体化平台对算法结果进行验证。该平台是集城轨列车牵引、制动、供电及信号多个子系统为一体的半实物仿真平台,可用于多车运行条件下的城轨列车供电系统、关键子部件、信号系统的一体化综合仿真试验。平台采用线性二次调节器LQR进行曲线跟踪控制,效果如图8所示。可以看出,该曲线与规划曲线基本贴近,偏差较小。为了更合理地评估算法结果,表5和表6分别示出目前已实现的一种单站间节能算法以及ATO一体化优化算法结果与公司现有ATO控车算法结果的全线路周转的牵引能耗与运行时间对比。可以看出,MILP算法在节省运行时间27.6 s的基础上还能保持14.7%的节能效果。相比较单站间定时节能优化算法,用MILP算法可以节约更多的牵引能耗;同时,若增加线路运行时间,则节能效果将会更好。图9给出了路网车一体化平台半实物仿真测试的界面图,由此清晰地看出能耗、运行时间等数据并判断控制算法效果。

图8 平阳-长沙火车南站间跟踪控制曲线Fig. 8 Tracking control train trajectory between Pingyang and South Changsha railway stations

图9 路网车一体化平台跟踪控制曲线界面Fig. 9 Interface of tracking control train trajectory on the integrated platform of road-network-train
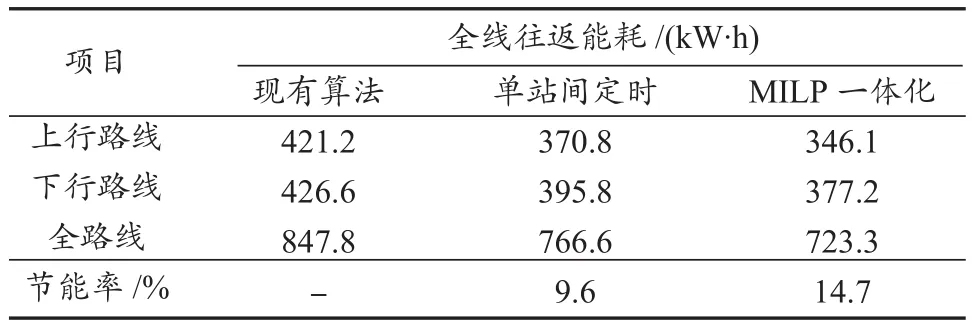
表5 全线往返能耗结果对比Tab. 5 Comparison of energy consumption between up direction and down direction lines

表6 全线往返运行时间结果对比Tab. 6 Comparison of running time between up direction and down direction lines
4 结语
本文针对城市轨道交通列车一体化节能运行曲线优化问题进行研究,选取时间和能耗为状态变量,牵引/制动力为控制变量,基于空间位置对模型进行离散处理,建立了一种考虑冗余时间分配和单站间定时节能一体化优化模型;通过PWA函数以及线性化等效法则,将原非线性模型转换为MILP模型,并通过Matlab调用CPLEX进行求解。基于长沙地铁4号线数据设计仿真案例对模型进行验证。仿真结果表明,采用本文所提出的基于MILP的城市轨道交通列车一体化节能运行曲线优化模型可以达到16.5%的节能效果。由于该模型尚未考虑再生制动能对能耗计算的影响,下一步将对结合再生制动能的节能策略开展列车运行仿真算法研究。

