单值中智语言集属性相关联的多属性群决策方法
冯 源,危 婷
(太原师范学院 数学系,山西 晋中 030619)
0 引言
1965年,Zadeh[1]提出了模糊集的概念,发表的Fuzzy Set奠定了模糊集理论的发展基础.之后Atanassov[2]提出直觉模糊集,它拓展了模糊集的概念,同时考虑了三方面的信息,包括隶属度、非隶属度和犹豫度.对于属性间存在关联性的这类问题,Xu[3]和Tan[4]将Choquet积分引入直觉模糊集上并进行了应用.徐泽水[5]系统研究了直觉模糊集的相关理论.但是由于直觉模糊集的隶属度和非隶属度只能取精确实数,所以不能处理不确定信息.Smarandache[6]将不确定度加入直觉模糊集提出了中智集的理论,再之后Wang 和 Smarandache[7]等在中智集理论的基础上提出了单值中智集的具体概念,并对它相关的运算规则和性质进行研究和讨论.为解决有关多属性决策问题,Ye[8-9]构造了单值中智集和区间中智集的交叉熵.对于单值中智集属性相关联的决策问题,韩莉莉[10]引入了Choquet积分来进行研究分析.
生活中存在许多评价并不能用精确的数字来表示,比如好、很好这类评价方式,关于这类评价,Zadeh[11]最早提出采用语言变量来描述偏好信息,并引发关注.谭春桥[12]引入Choquet积分对语言环境下的决策进行了研究应用,刘宁元[13]又将语言集拓展为直觉语言集,并结合TODIM方法对相关决策问题进行了讨论.Ye[14]在基于中智集的概念又引申提出了单值中智语言集;郭子雪[15]、范建平[16]对单值中智语言环境下的决策方法进行了研究.Gomes和Lima[17]提出的TODIM决策方法通过比较各个方案的优势度再计算出全局优势来判断方案的优劣.
基于此,首先给出了关于单值中智语言集的相关概念以及它的定义运算,然后定义了单值中智语言集的Choquet积分算子并讨论其性质,再结合TODIM方法给出了考虑决策者心理行为属性相关联的多属性群决策方法,最后结合一个算例进行运用,从而证明此法的有效性与可行性.
1 基本知识
首先给出单值中智语言集的基本概念,如下所示:
定义1[14]设X={x1,x2,…,xn}为给定的论域,S={s1,s2,…,sl}为有限且完全有序的离散语言术语集,单值中智语言集A定义为
A={
其中,xi∈X,sθA(xi)∈S,TA(xi)∈[0,1],IA(xi)∈[0,1],FA(xi)∈[0,1].TA(xi),IA(xi),FA(xi)分别表示xi在X为sθA(xi)的真实度,不确定度,谬误度,对任意的xi∈X,均有0≤TA(xi)+IA(xi)+FA(xi)≤3.A可以看作是单值中智语言数的集合,若A中只有一个元素则可称A为单值语言数.
定义2[15]设a=〈sθ(a),(T(a),I(a),F(a)〉是单值语言数,那么a的得分函数s(a)定义为
s(a)=sθ(a)(T(a)+1-I(a)+1-F(a))
精确度函数h(a)定义为
h(a)=sθ(a)(T(a)-F(a))
根据定义2所给的得分函数和精确度函数,可以得到如下两个单值中智语言数的比较方法.
定义3[15]设a=〈sθ(a),(T(a),I(a),F(a)〉和b=〈sθ(b),(T(b),I(b),F(b)〉为两个单值中智语言数,那么他们之间的比较方法如下:
(I)如果s(a)>s(b),则a大于b,记为a≻b.
(II) 如果s(a)=s(b),h(a)=h(b),则a等于b,记为a~b.
(III) 如果s(a)=s(b),h(a) 定义4[14]设a=〈sθ(a),(T(a),I(a),F(a)〉和b=〈sθ(b),(T(b),I(b),F(b)〉为两个单值中智语言数,λ>0,那么单值中智语言数的运算定义如下: (II)a⊗b=〈sθ(a)×θ(b),(T(a)T(b),I(a)+I(b)-I(a)I(b),F(a)+F(b)-F(a)F(b)〉 (III)λa=〈sλθ(a),(T(a),I(a),F(a)〉 (IV)aλ=〈sθλ(a),(Tλ(a),1-(1-I(a))λ,1-(1-F(a))λ)〉 为解决单值中智语言环境下属性间相关联的群决策问题,需要运用Choquet积分,在这里尝试提出单值中智语言集的Choquet积分平均算子.首先为了描述决策属性的重要性以及决策属性间的交互作用,在这里我们采取λ测度来描述.λ测度的定义如下: 定义5[10]设λ∈(-1,∞),称非空有限集X上的集函数gλ:P(X)→[0,1]为λ测度,如果gλ(X)=1,且对任意两个不交子集A,B,有 gλ(A∪B)=gλ(A)+gλ(B)+λgλ(A)gλ(B) 如果λ=0,则为经典的概率测度. 根据定义4的运算规则我们可定义出单值中智语言Choquet积分平均算子. 定义6设αi= (1) 它是Ωn到Ω的映射,其中Ω为单值中智语言集;(·)为集合X上的一个置换,使得α(x(1))≤…≤α(x(n)),X(i)={x(i),…,x(n)},X(i)={x(i),…,x(n)},X(n+1)=φ.当λ=0,即X中的元素互相独立时,单值中智语言Choquet平均算子即为单值中智语言有序加权平均算子. 定理1设αi=〈sθ(αi),(T(αi),I(αi),F(αi)〉(i=1,2,…n)为定义在X上的一组单值中智语言数,μ为X={x1,x2,…,xn}上的λ测度,则上式的计算结果仍然是单值中智语言数,即 (2) 其中,(·)为集合X上的一个置换,使得α(x(1))≤…≤α(x(n)),X(i)={x(i),…,x(n)},X(n+1)=φ. 此等式用数学归纳法即可证得. 同样根据定义4的运算规则我们可定义出单值中智语言Choquet积分几何平均算子. 定义7设αi= (3) 它是Ωn到Ω的映射,其中Ω为单值中智语言集;(·)为集合X上的一个置换,使得α(x(1))≤…≤α(x(n)),X(i)={x(i),…,x(n)},X(n+1)=φ.当λ=0,即X中的元素互相独立时,单值中智语言Choquet积分几何平均算子即为单值中智语言有序加权几何平均算子. 定理2设αi=〈sθ(αi),(T(αi),I(αi),F(αi)〉(i=1,2,…,n)为定义在X上的一组单值中智语言数,μ为X={x1,x2,…,xn}上的λ测度,同理也可得上式的计算结果仍然是单值中智语言数,即 (4) 其中,(·)为集合X上的一个置换,使得α(x(1))≤…≤α(x(n)),X(i)={x(i),…,x(n)},X(n+1)=φ. 我们可以证得上述算子具有以下性质: 证明: 即证,同理可以证明SVNLCWG的置换不变性. 性质2:若单值中智语言数αi=α(i=1,2,…,n),则 SVNLCWA(α1,α2,…,αn)=α;SVNLCWG(α1,α2,…,αn)=α 证明: 即证. 证明: SVNLCWA(α′1,α′2,…,α′n)=SVNLCWA(α′1,α′2,…,α′n)≤ 即证.同理可证SVNLCWG的单调性. 为了方便表示计算步骤,先给出如下假设: (5) (6) 步骤3:根据属性集的模糊测度μ(am),根据式(6)计算出λ2,以及属性集合的模糊测度μ(Am),并由定义2中的得分函数计算出每个属性下群体决策矩阵R的得分函数s(rij) 步骤4:计算方案xi的优势度矩阵Φ=[φ(xi,xt)]n×n.对于属性Aj,备选方案xi与xt的优势度计算如下: (7) (8) (9) μ(aσ(j))=μ(Aσ(j))-μ(Aσ(j+1)),Aσ(j)={aσ(j),…aσ(m)},μ(Aσ(m+1))=0 式子(8)中θ为损失规避系数,θ越小,表明决策者的损失规避程度越高.这里的d为单值中智语言集间的Hamming距离,由Hamming距离的概念我们可以定义两个单值中智语言数a=〈sθ(a),(T(a),I(a),F(a)〉和b=〈sθ(b),(T(b),I(b),F(b)〉间的Hamming距离为: d(a,b)=|θ(a)T(a)-θ(b)T(b)|+|θ(a)I(a)-θ(b)I(b)|+|θ(a)F(a)-θ(b)F(b)| 步骤5:计算每个方案全局优势度. (10) D(1)= D(2)= D(3)= 步骤1:规范化决策矩阵,由于都是效益型属性,所以不需要规范化. 步骤2:根据专家的模糊测度以及式子(6)计算出λ1以及专家间的关联模糊测度: λ1=-0.443,μ(e1,e2)=0.729,μ(e1,e3)=0.729,μ(e2,e3)=0.729,μ(e1,e2,e3)=0.729, 然后利用SVNLCWA算子进行计算,即式(2)对专家的决策矩阵R(k)n×m进行集结,得到 步骤3:根据属性集的模糊测度由式(6)计算出λ2=-0.2371以及属性集合的模糊测度 μ(c1,c2)=μ(c1,c3)=μ(c2,c3)=0.579,μ(c1,c2,c3)=0.839 μ(c1,c2,c4)=μ(c1,c3,c4)=μ(c2,c3,c4)=0.752,μ(c1,c2,c3,c4)=1 以及得分函数 步骤4:根据式(7)计算优势度矩阵 步骤5:根据式(10)计算每个方案的全局优势度ζ(x1)=0,ζ(x2)=1,ζ(x3)=0.774,ζ(x4)=0.417,因为x2≻x3≻x4≻x1,所以供应商2为最优的供应商. 本文定义了单值中智语言集的Choquet积分算子来解决单值中智语言集属性相关联的情况,然后结合TODIM方法来进行相关的多属性群决策问题.本文算例是在文献[10]的算例基础上进行改编,引入语言集以及专家的模糊测度,运用此文提出的方法来进行解决,同样我们得到供应商2为最优选择,供应商1为最差选择,这与原算例结果相同,这表明虽改变一定的评判数值但并未改变结果,充分说明了供应商2综合实力的优等性与供应商1的差等性,中间两个供应商的综合实力判断略有不同,这即是引入语言集以及对专家的权重改变造成的.同时也证明了本文所提方法的有效性与可行性. 对于直觉模糊语言集的研究文章已经比较多,但将语言集引入中智集内的相关研究还比较少,在此文我们对属性间存在相关性的单值中智语言集进行了研究,并结合TODIM方法来做决策判断,在未来我们还可以联系更多的方法,例如逼近理想排序法(TOPSIS),选择消去法(ELECTRE)等,不断丰富对于单值中智语言环境下的群决策理论.2 单值中智语言Choquet积分算子

3 单值中智语言环境下属性相关的群决策方法

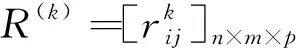



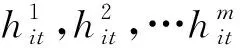
4 算例分析

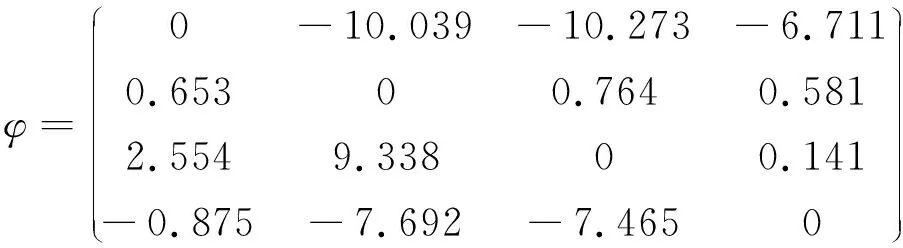
5 总结

