圆形均匀带电薄板电场的数值积分和可视化
周群益,莫云飞,侯兆阳,周丽丽
(1.广州理工学院 通识教育学院,广东 广州,510540;2.长沙学院 电子信息与电气工程学院,湖南 长沙,410022;3.长安大学 理学院应用物理系,陕西 西安,710064;4.赣南医学院 医学信息工程学院,江西 赣州,341000)
均匀带电圆形薄板电场的计算比较复杂,一般只推导了轴线上的电势和电场强度的公式[1–5]。这个问题没有一般的解析解,少有研究这个问题的文献。本文利用环电荷的场强公式,建立了电势和电场强度的积分公式,用MATLAB的数值积分方法解决了计算问题,并绘制电势和场强的曲面、二维等势线和电场线。
1 圆板电荷的电势和场强
(1)电势。在直角坐标系中,圆环电荷的电势为[7–9],其中:Q是圆环的带电量,默认为Q>0。RM是圆环上的点到场点的最大距离;K(m)是第一类完全椭圆积分[10–11],m是模数(a是圆环的半径)。
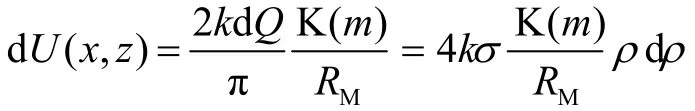
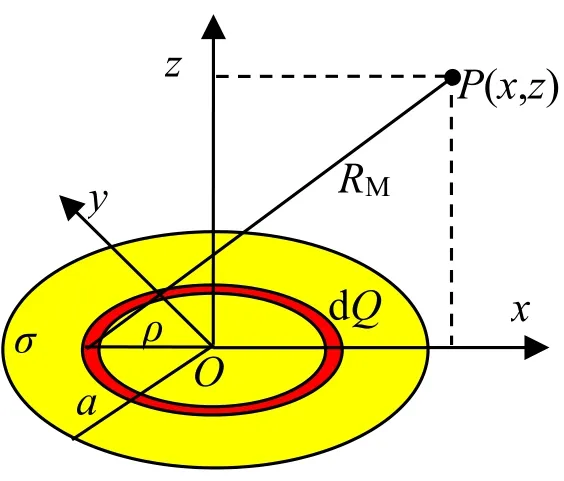
图1 圆板电荷电势的示意图
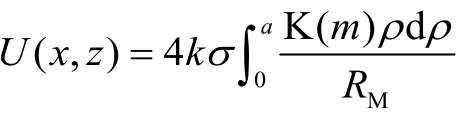
当x=0时,最大距离为,模数为m=m(0,z)=0,第一类完全椭圆积分为K(0)=π/2。圆板在轴线上产生的电势为
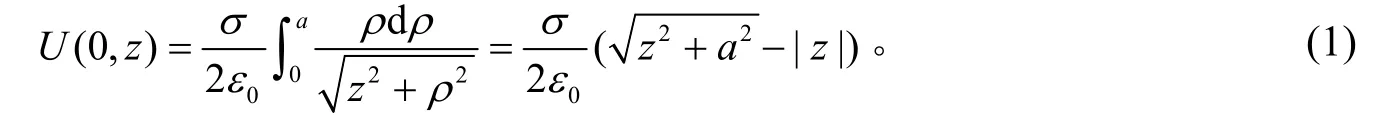
当z→∞时,U(0,z)→0,即:无穷远处是零势点。当z=0时,可得圆心处的电势

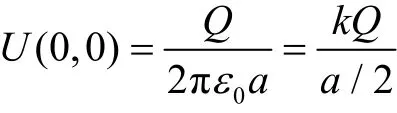
当x=0时,第二类完全椭圆积分为E(0)=π/2。圆板在轴线上产生的场强分别为Ex=0,。这是电磁学中的结果。当a→∞时,可得无限大带电薄板的场强。
2 公式的无量纲化
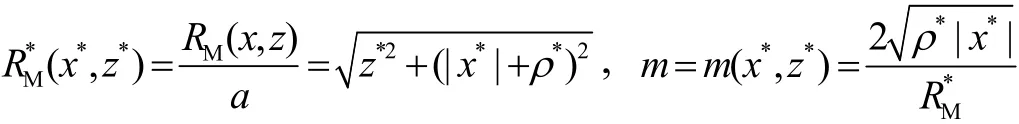

3 电场的可视化
利用MATLAB设计程序,用数值积分方法很容易求出电势和电场强度的积分值(见附录)。
(1)如图2(a)所示,均匀带电圆板在轴线上的电势U(0,z)是偶对称曲线,z=0处是一个尖点,表示圆心的电势最高U(0,0)=2U0;在离圆心较远的地方,带电圆板产生的电势接近于点电荷产生的电势。如图2(b)所示,均匀带电圆板在轴线上的场强Ez(0,z)是奇对称曲线,在z=0处,Ez(0,0)=0,这是圆心的场强;在z=0+处,Ez(0,0+)=2E0,这是上表面的场强;在z=0-处,Ez(0,0-)=-2E0,这是下表面的场强,负号表示方向相反;在离圆心较远的地方,带电圆板产生的场强接近于点电荷产生的场强。
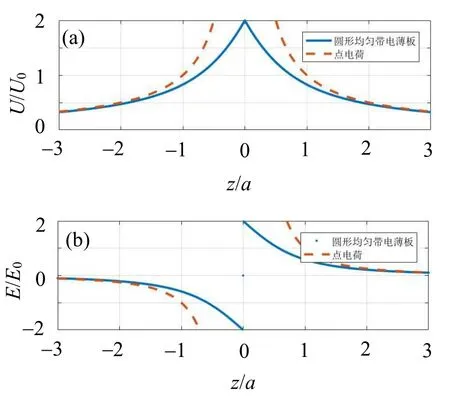
图2 均匀带电圆板在轴线的电势(a)和场强(b)
(2)如图3所示,均匀带电圆板的电势U(x,z)是一个单峰曲面,是关于x和z的偶函数;三维等势线分布在曲面上,沿着Oz方向的电势U(0,z)曲线也分布在曲面上。点(0,0)处的电势最高,当z=0而x在区间[-a,a]的电势U(x,0)并不是常数,说明圆板表面并不是一个等势面。
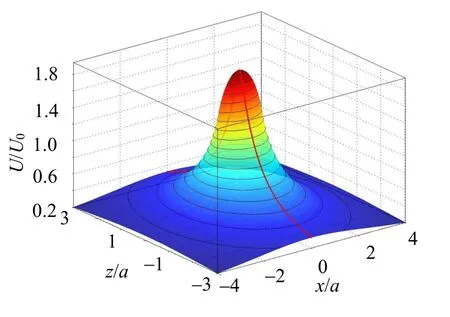
图3 均匀带电圆板的电势
(3)如图4所示,圆板电荷场强的x分量Ex(x,z)是关于x的奇函数,关于z的偶函数;Ex在(±a,0)处各有1个尖锐的“峰”和“谷”,说明两处的Ex很大而方向相反。当x=0时,Ex=0的直线在曲面上。
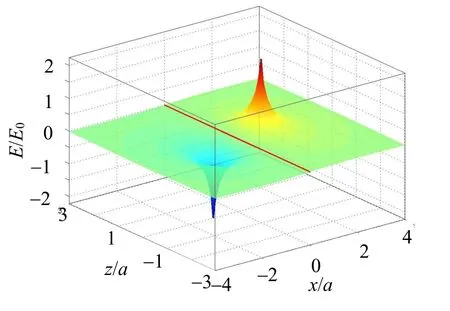
图4 均匀带电圆板场强的x分量
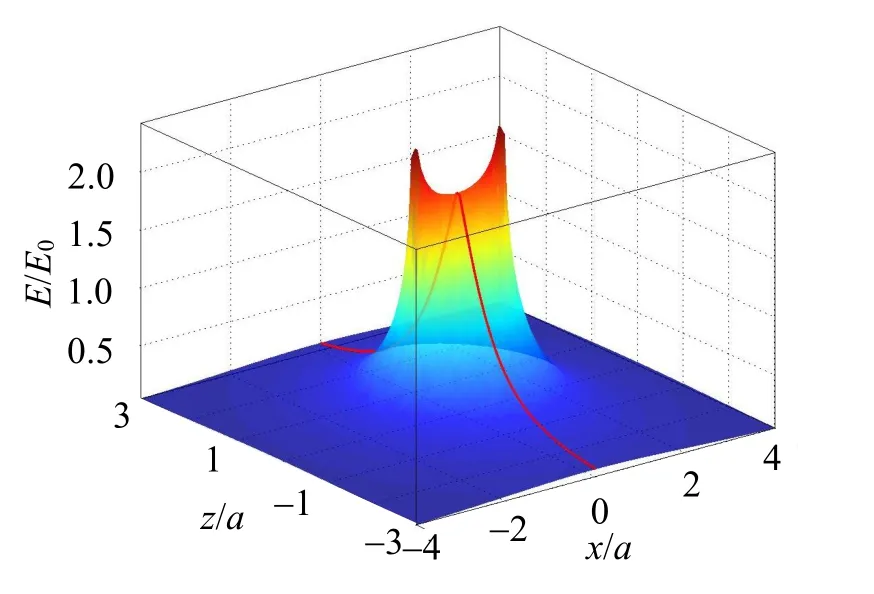
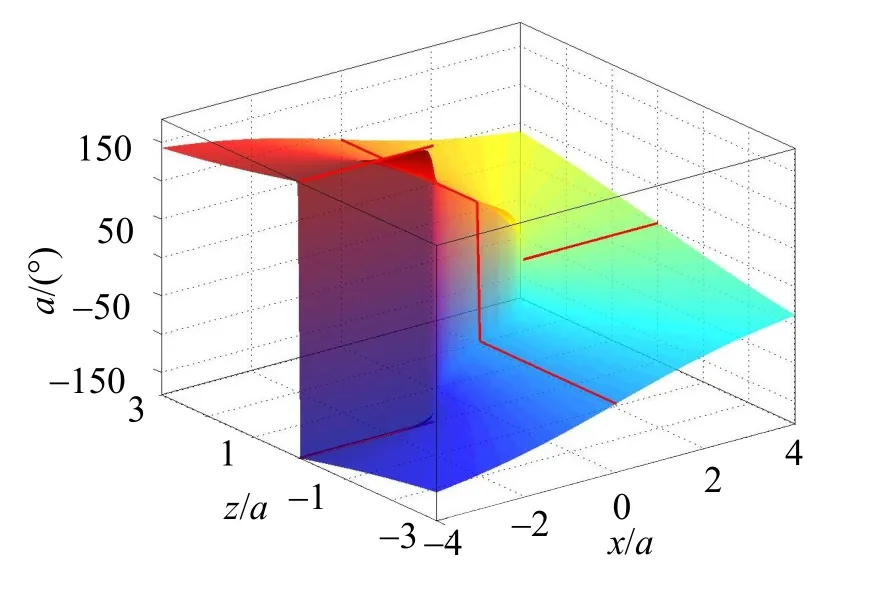
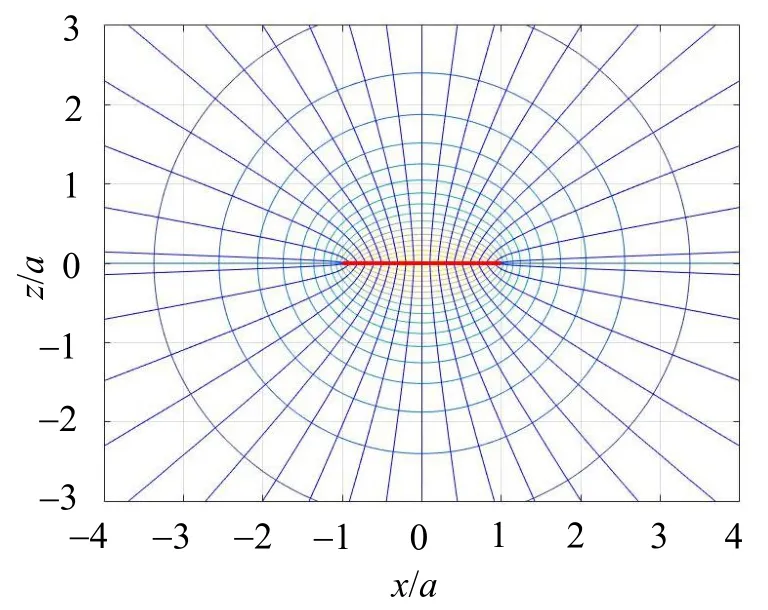
(4)如图5所示,场强的z分量Ez(x,z)是关于x的偶函数,关于z的奇函数;当-a 图5 均匀带电圆板场强的z分量 (5)如图6所示,合场强E的大小E(x,z)是关于x和z的偶函数,曲面在(±a,0)处有一对“犄角”,这是因为(±a,0)处的场强E比较大。当x=0时,E=|Ez|的曲线在曲面上,这是轴线上场强的大小,(0,0)处是一个鞍点。 图6 均匀带电圆板的合场强 (6)如图7所示,合场强E的方向角α随着Oxz平面的极角φ(极轴是x轴,逆时针方向为正)的增加而增加,在φ=0且x>a处,α=0;在φ=±π/2处,α=±π/2;在φ=π且x<-a处,α发生从π到-π的跃变,这是因为π和-π是同一角度;在圆板的两边(-a 图7 均匀带电圆板合场强的方向 (7)如图8所示,二维等势线就是图2中的三维等势线在Oxz平面上的投影。电势较低的等势线包围圆板,电势越低,等势线越圆;电势较高的等势线穿过圆板,说明均匀带电的圆板表面不是等势面。除了轴线上之外,圆板表面的电场线与表面并不垂直,也说明圆板表面不是等势面。电场线与等势线垂直,在点(±a,0)附近,电场线比较密集,说明两处的场强比较大。 图8 均匀带电圆板的等势线和电场线 本文建立了圆板电荷的电势和电场强度的积分公式,将公式无量纲化,用MATLAB的数值积分的方法计算数值,用简单的指令绘制了电势和电场强度的分布曲面和二维等势线和电场线,说明了电场分布的规律。当积分公式没有解析解时,数值积分是十分有用的方法。由绘制的图形可知:均匀带电圆板并不是等势面(体),场强并不与表面垂直,因而不是导体。圆形带电导体薄板的电势和电场还需要深入研究。 附录: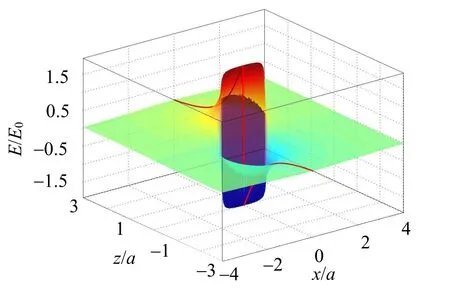
4 结束语



