一类非自治时滞Mackey-Glass推广模型的吸引性分析

周启元,曹前,杨刚

(1.湖南文理学院 数理学院,湖南 常德,415000;2.湖南工商大学 理学院,湖南 长沙,410205)

时滞动力学模型的复杂行为一直是物理学、生物数学、网络系统等领域的研究热点[1–7]。早在1977年,为了研究人类疾病的调控机制,Mackey和Glass[8]建立了著名的时滞微分方程

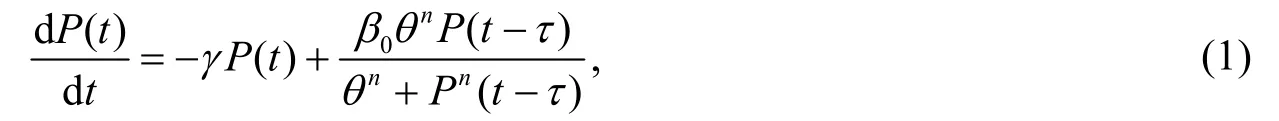
来描述单峰生产速率下的造血过程,称之为 Mackey-Glass模型。从生物学角度来说,P(t)表示成熟循环细胞的密度,n>0,γ,β0,θ为正常数,分别表示破坏速率、最大生产率和形状参数,τ表示循环过程中骨髓产生的细胞从出生到发育成熟所需的时间。因为系统(1)再现了正常呼吸和异常呼吸状态下造血过程的某些定性特征,从而引起了学术界的广泛关注,并获得了有关其正解的存在性、分岔、持久性、有界性、振动性以及这类方程及其类似模型的局部稳定性的诸多成果[9–12]。

由于在造血过程中,骨髓所产生的细胞从出生到发育成熟所需的时间(称为成熟时滞)和孵化时间(称为孵化时滞)一般是不相同的,因此系统(1)很自然地被推广为以下具有2个互异时变时滞的非自治时滞微分方程形式[13]

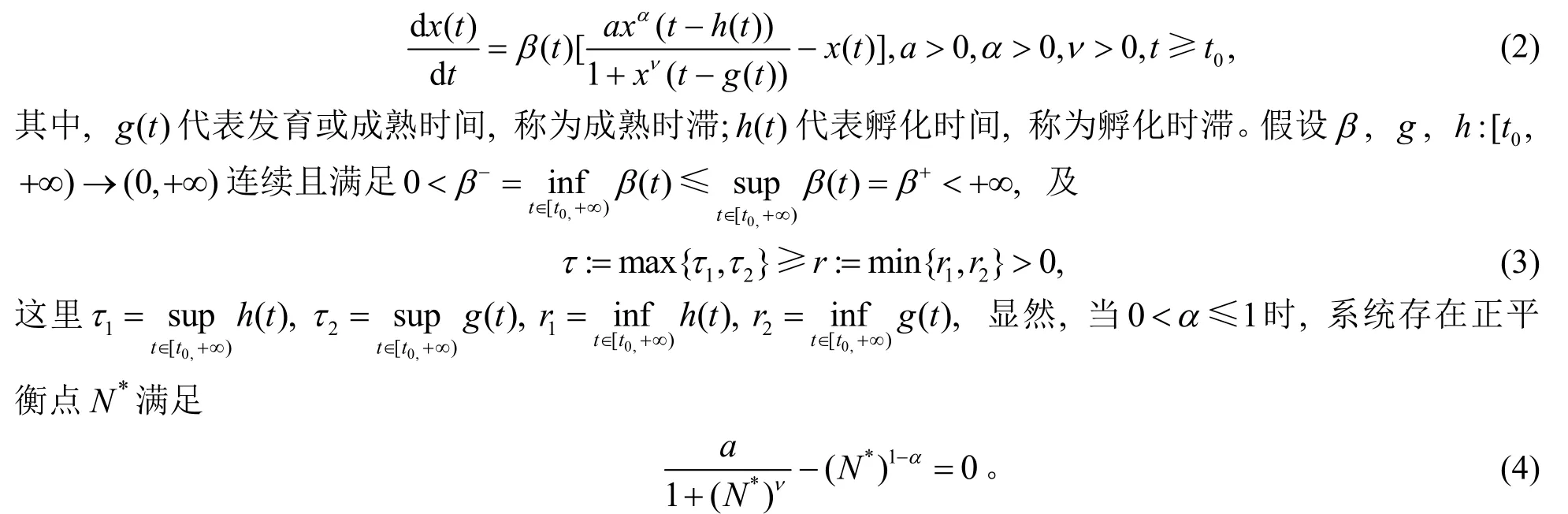
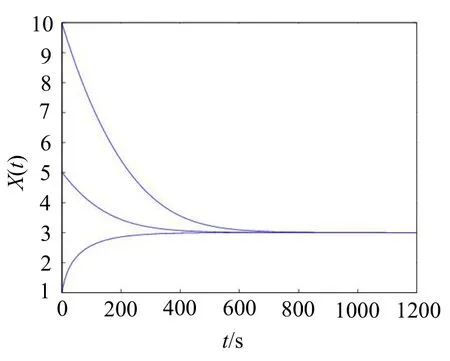
在系统(2)中引入2个互异时滞g(t)和h(t)后,其动力学行为比只具有单个时滞τ的系统(1)要复杂得多。Berezansky和Braverman在文献[13]中用实例表明,同一个非线性函数中的2个互异时滞会导致系统持续震荡甚至会产生混沌现象。此时,具有2个互异时滞的反馈函数应该被视为二元函数,这给研究带来了许多实质性的困难。近年来,已有众多学者对具有2个互异时滞的微分系统进行了研究[14–23]。但到目前为止,对系统(2)的全局稳定性研究仍然是一个具有挑战性的公开问题[13],研究成果非常少见。最近,文献[14]的作者对α=1时的系统(2)进行了研究,在a>1条件下,建立了其关于正平衡点的非震荡解的全局收敛性,同时在01时系统(2)的非震荡解的全局收敛性条件;在α=1,0

1 系统解的存在性

证毕。

2 系统解的稳定性

3 数值模拟

在本节将提供2个数值实例,并通过图形比较来验证本文所建立的理论结果的有效性和可行性。考虑如下具有2个不同时滞的Mackey-Glass方程:

由定理1和定理2,不难看出系统(16)关于其唯一正平衡点N*=4的非振荡解都收敛到*N。同时,定理4表明系统(17)全局指数稳定。2个数值实例的计算机模拟如图1和图2所示,其所示解的轨迹有力的证实了本文结果的正确性和有效性。

图1 系统(16)的数值解

图2 系统(17)的数值解

附注3需要指出的是,关于具有互异时滞的非自治Mackey-Glass推广模型(2),在以往文献中还没有建立与时滞无关的有关其渐近性态的判据。显然,上述文献[8–23]中的所有结果都不能证明式(16)和(17)的解的收敛性或稳定性。

4 结论

具有2个互异时滞的Mackey-Glass模型的稳定性条件是Berezansky和Braverman在文献[13]中提出的公开问题,目前还没有得到很好的解决。本文主要研究了具有2个互异时变时滞的Mackey-Glass推广模型的正平衡点关于其所有非振动解的吸引性。利用波动引理和微分不等式技巧证明了同一生育函数中的2个互异时滞对非振荡解的收敛性没有影响。同时,还建立了其零平衡点的局部稳定性和全局指数稳定性条件。所得到的结果有力的推动了上述公开问题的解决。此外,本文还给出了2个数值算例,证实了本文所建立结果的有效性。特别地,本文提出的方法为研究其它具有2个互异时滞的种群动态模型的渐近行为提供了借鉴。