基于偏最小二乘支持向量机模型的个人信用评估研究

梁小林,柳映堂,梁曌,欧阳冰玉

(长沙理工大学 数学与统计学院,湖南 长沙,410114)

在一个发达的金融体系中,如何准确有效地识别客户潜在信用风险是金融界普遍关心的问题,特别是新冠肺炎的爆发对全球经济产生重大影响,如何对企业与个人进行有效的信用评价至关重要。早在1941年,Durand[1]运用判别分析方法研究分期付款中的不良贷款人群,Eisenbeis[2–3]将该方法推广到一般的信用评价问题中。Martin[4]应用逻辑回归模型研究了银行危机预警系统,显著提升了分类精度。针对8个典型的信贷数据库,Gestel等[5]提出了17种不同的信用评分模型,结果表明,支持向量机(SVM)模型的分类性能最佳。魏秋萍等[6]采用偏最小二乘(PLS)建立信用评分模型,解决了变量间多重共线性问题,李佳欣[7]基于逐步Logistic回归的分类算法进行个人信用风险分析,提高了分类准确率。但是,当变量过多时,SVM的训练时间将变得漫长,不仅效率降低,而且容易导致超平面不准确(Min)[8]。这种现象在统计学上被称为“维数灾难”(Anderson[9])。由于偏最小二乘回归在非线性建模时表现较差,因此本文将联合偏最小二乘与支持向量机建立集成模型,并利用该模型预测客户的违约行为。另外,本文将使用AUC值和相对误差频率分布作为评价指标对各模型进行对比实验。

1 信用评分与模型建立

对于给定的信用数据集(Xi,yi),i=1,2,…,N,其中Xi=(xi1,xi2,…,xip)表示客户i的个人信息;如果客户i信用良好,则定义标签yi=1,否则定义标签yi=-1,I={i|yi=1,i∊N}为好客户集,J={j|yj=-1,j∊N}为坏客户集。信用评估目标是通过客户的个人信息Xi推断该客户是否信用良好。

1.1 支持向量机(SVM)模型

SVM模型是找一个分类超平面t=wTx+b,使分类“间隔”最大,即求解二次规划

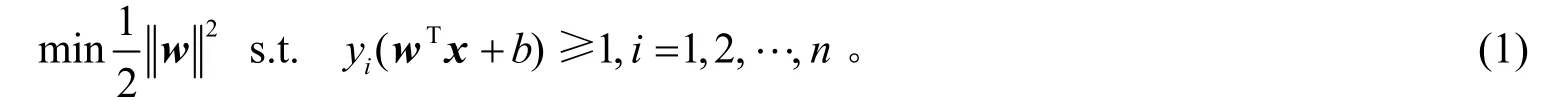
对于线性不可分的情形,需要加入软间隔以及惩罚系数C,分类问题变为如下二次规划

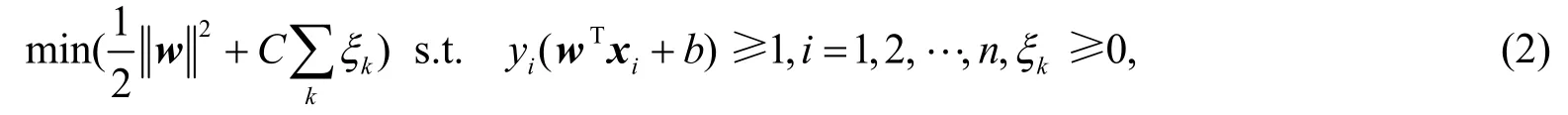
利用拉格朗日乘子法,式(2)可以转化为

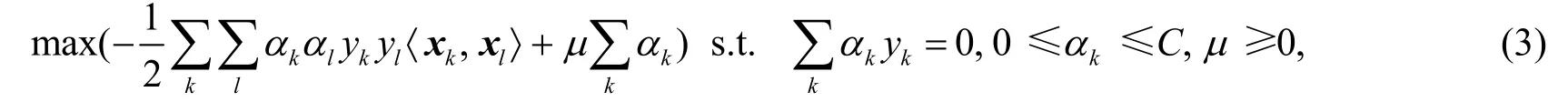
定义核函数K(xk,xl)=〈φ(xk),φ(xl)〉代替〈xk,xl〉,式(3)化为如下规划问题

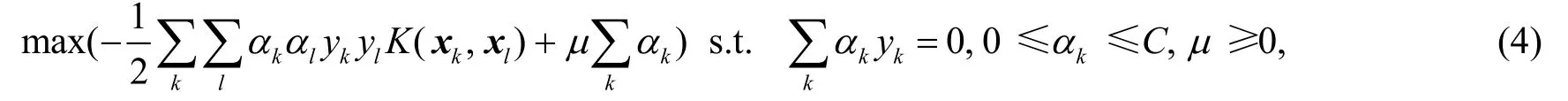
式(4)可用于解决非线性分类问题。

1.2 偏最小二乘(PLS)回归

偏最小二乘回归先利用决策变量与响应变量的相关性提取特征,然后再建立回归方程。

设e0i,F0分别为xi,y的标准化向量,E0=(e01,e02,…,e0p)T,记t1是E0的第1个成分,t1=E0w1,记a1是F0的第1个成分,a1=F0c1。

在PLS回归中,要求成分t1与成分a1的协方差最大,即

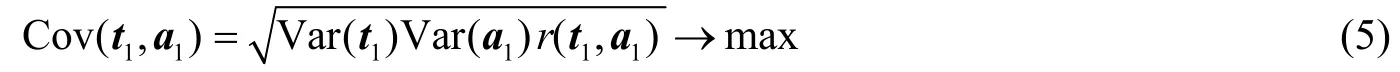
即求解如下优化问题

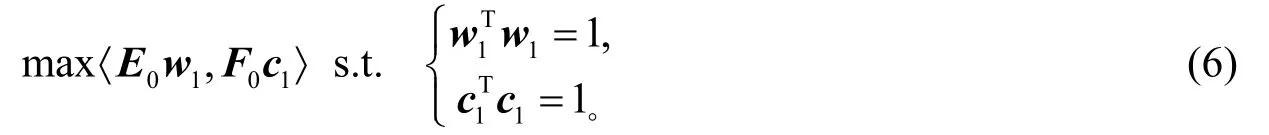
利用拉格朗日乘子法求解式(6),即可得到第1个成分

E0和F0分别对成分t1和成分a1求回归

利用残差矩阵重复式(6)～(8)可得第k成分tk,在利用交叉有效性原则获得成分个数。

1.3 偏最小二乘支持向量机模型

模型先通过PLS获取特征成分进行降维,再利用各特征成分进行SVM建模,分为4步:

(1)将初始数据进行标准化,得到x1,x2,…,xn;

(2)运用PLS提取特征。经计算得到Ttrain=[t1,t2,…,tn],P=[p1,p2,…,pn]和W=[w1,w2,…,wn];

(3)SVM建模。对数据集(Ttrain,ytrain)进行SVM建模训练,得到最优参数αi,i=1,2,…,k和偏置b;

(4)分类预测。对于待预测的样本Xtest,通过式(9)计算得到Ttest,

利用第(3)步建立的SVM模型获得分类结果。

2 实验及结果

2.1 数据来源与描述

本实验从UCI机器学习库下载台湾信用卡客户信息数据。该数据集总样本量数为2 000,其中1 500例为好客户(正常客户),500例为坏客户(违约客户),无删失数据。

每个客户提供了23种不同信息,包括性别,婚姻,学历,其中第4至第9个变量为该客户过去的付款记录,共追踪了2015年4月至9月的付款情况,-1为按时还款;1为延迟1个月付款;…;8为延迟8个月还款;9为延迟9个月及以上还款。另有14个定量变量分别为贷款额度,客户年龄,过去6个月(2015年4月至9月)的账单金额(共6个变量),过去6个月的付款额度(共6个变量)。

2.2 数据的预处理

对于定性变量,通过引进虚拟变量进行量化,例如,性别变量有2个属性,这里将定义2个虚拟变量:一个是性别_0,另一个是性别_1。其他定性变量作类似定义。使用该方法将使维度从23增加到93维。

2.3 数据降维

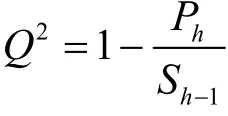
2.4 评估方法

2.4.1 交叉验证

为了提高模型的泛化性能,本文采用交叉验证方法验证错误率。将数据集随机的等分为4个不相交的子数据集。将其中3个子数据集训练逻辑斯蒂回归和SVM模型,并用第4个子数据集验证模型。

2.4.2 评估标准

信用评估问题主要关注分类的准确性。本文采用分类准确率(包括ACC,TPR与TNR)[10]、AUC和相对误差频率图作为评判标准。

首先,Fawcett(2006年)[11]在研究机器学习算法时发现,AUC测量对阳性误差更为敏感,这个发现是有意义的,因为在评估客户是否信用良好时,将一个坏客户判断为好客户比将一个好客户判断为坏客户风险成本更大。因此本文选择AUC作为模型的评价标准。

其次,相对误差频率图能显示各分类模型之间的表现差异。相对误差定义为RE=i-yi,其中:i表示第i个样本的预测值,易知,相对误差值分布集中在0值附近,则模型预测值与实际观察值误差低,预测效果好,因此本文选择相对误差频率图作为模型的另一评价标准。

2.5 模型对比分析

2.5.1 降维效果

首先,逻辑斯蒂回归和SVM的性能比较。从表1可知,在降维前SVM的效果要比逻辑斯蒂回归稍差,但在模型降维后,SVM的准确率与真阴率均超过了逻辑斯蒂回归模型,表明降维对SVM的性能有提升。虽然SVM真阳率比逻辑回归稍差,但就信用评估而言,更重要的是对坏客户的准确判断。

其次,PLS降维对逻辑斯蒂回归模型的影响。虽然PLS降维后逻辑斯蒂回归模型的真阳率有了明显的提高,但并不比原始模型有更好的真阴率。这可能是由于在模型降维后,缺少足够多的变量使其具有线性关系。因此本实验表明,通过PLS降维不能改善逻辑回归模型的性能。

最后,PLS降维对SVM模型的影响。从表1中列1和列3发现,通过偏最小二乘降维后的支持向量机模型的性能在有效性、稳定性以及准确性3个方面都有改进,因此有理由推断,对于信用评估问题,偏最小二乘降维能改进SVM的性能。

2.5.2 模型对比

下面将分析PCA-SVM,PLS-SVM等几种不同的组合模型,寻找最佳的信用评估模型。

首先,PCA-SVM模型与PLS-SVM模型的性能比较。由表1可知,在PLS与PCA降维对SVM性能的影响方面,前者比后者的效果更好。同时,PLS-SVM比原始维数的SVM的准确率更高,表明降低维度的确能提高分类器的性能。

其次,PLS-SVM与PLS-LR模型的精度比较。如表1中列3所示,相比于逻辑斯蒂回归模型,PLS降维更适用于SVM模型。两个模型的真阳率非常接近,但由于坏客户的识别度更为重要,因而从真阴率的角度考虑,PLS-SVM模型比PLS-LR模型具有更高的准确性。

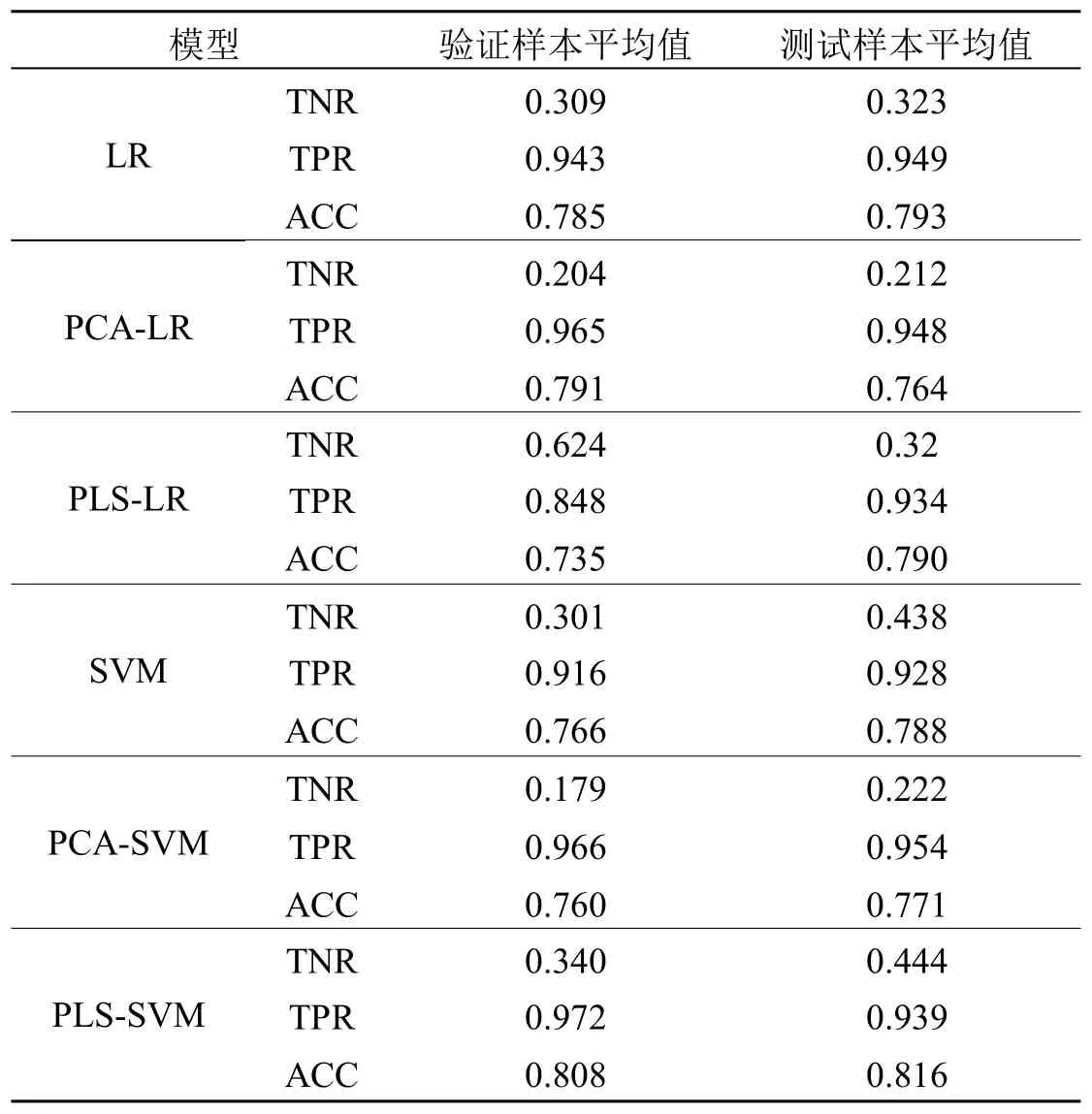
表1 各模型结果比较表

为了更进一步的比较组合模型的准确性,本文画出了不同模型的ROC图(图1),从ROC图可知,虽然没有哪一个组合模型的效果特别占优,但PLS-LR模型略弱,PLS-SVM模型略强,而且PCA的降维方法同时降低了2种分类器的AUC值(见表2)。因此,PLS-SVM是信用评分问题中最有效的方法。

表2 各模型AUC值

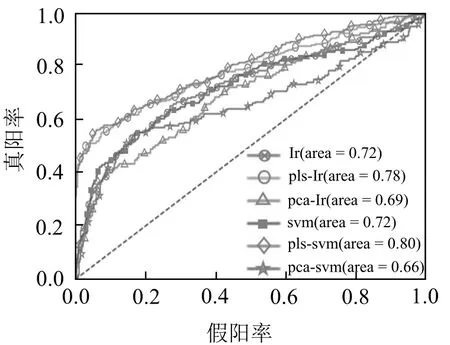
图1 各模型验证数据集ROC曲线图

此外,本文还对比了各组合模型的相对误差集中度,图2与表3表明采用PLS-SVM进行信用评估预测效果更佳。

表3 各模型在不同区间相对误差频率

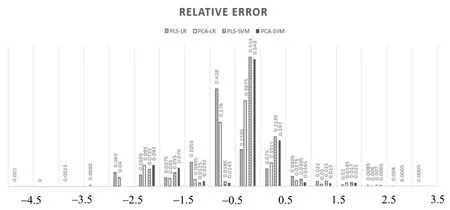
图2 各模型相对误差频率分布图

由相对误差频率分布图可知:对于模型PLS-SVM相对误差频率在[-0.5,0.5)区间里的样本超过76.65%;对于模型PCA-SVM,其样本占比为73.9%;其余模型其样本占比均未超过50%;说明PLS-SVM模型精密度较高。

3 结论

目前在信用评分方法上,维数灾难问题时常出现,不仅影响分类器的准确度,也降低了分类器的效率。本文提出的PLS-SVM组合信用评估模型预测精度比原始SVM有所提升,说明PLS方法能够降低变量间的相关性,结合SVM建模可以有效提高整体预测能力。另外,本文提出的相对误差频率分布可以直观显示预测值和真实值之间的差异与集中趋势,能准确反映模型的精密度。