凸度量空间中的广义凸性*
甘庆龄, 旷华武**, 杨光惠
(贵州大学 数学与统计学院,贵阳 550025)
0 引 言
凸集与凸映射、广义凸集与广义凸映射,分别是凸性理论和广义凸性理论的主要研究内容之一,在线性规划、无约束优化、约束优化、多目标规划、博弈论等最优化理论,以及不动点理论、非线性分析等研究中有非常重要的应用。有关广义凸性的研究可参考文献[1-9]。在通常意义下,例如在Rn中,凸函数、拟凸函数等概念是基于基础线性空间中的标准凸结构W(x,y,λ)=λx+(1-λ)y[1]。因此,关于凸性与广义凸性的研究,通常在线性空间中进行[1-3,7-9],在没有线性结构的度量空间中,相关理论较少。另一方面,正如线性空间,度量空间也是数学中常见的基本空间之一。因为度量空间不必具有线性结构,不一定能像线性空间一样引进标准的凸集、凸函数等概念,所以能否突破这种限制,即能否在度量空间中引入某种结构,使它具有线性空间中标准凸结构的某些性质,从而可以在度量空间中定义“凸集”与“凸函数”等,是值得探讨的。
1970年,Takahashi[4]首次在度量空间中引进了凸结构,命名这类度量空间为凸度量空间,并介绍了凸度量空间中的一些基本概念和基本理论,推广了一些不动点定理;2016年,Abdelhakim[5]在凸度量空间首次引入了W-凸函数与W-严格凸函数概念,讨论了其性质,建立了一个W-凸函数的判别准则,获得了两个不动点定理;2017年,Jafari[6]在凸度量空间首次引入了W-拟凸函数,研究了平衡问题。注意到:第一,自Takahashi定义凸度量空间以来,对凸度量空间中不动点定理的研究较多[4-6,11],对凸度量空间中广义凸集与广义凸函数的研究较少;第二,与线性空间比较,例如与文献[1]比较,文献[4-6]中对广义凸函数类型的定义是不完善的,W-凸函数的判别准则仅有一个且条件较强。本文的目的是应用研究凸性及广义凸性的基本思想方法,尤其是文献[1]及[2,7]中的基本思想方法,针对凸度量空间中的抽象凸结构,引进3种新广义W-凸函数,研究6种广义W-凸函数相关问题,包括中间点W-凸函数的性质、稠密性定理及其应用、W-凸函数的一些判别准则等。
1 预备知识
定义1[4]设(X,d)是度量空间,W:X×X×[0,1]→X是映射,如果d(z,W(x,y,λ))≤λd(z,x)+(1-λ)d(z,y),∀x,y,z∈X,λ∈[0,1],则称W是(X,d)上的一个凸结构,(X,d,W)是一个凸度量空间。
定义2[4]设(X,d,W)是凸度量空间,K⊆X,若任意x,y∈K,任意λ∈[0,1],有W(x,y,λ)∈K,则称K是W-凸集。
双曲空间(hyperbolic space),包括具有线性结构的赋范线性空间,不具有线性结构的CAT(0)空间和Busemann凸空间,是凸度量空间。特别地,赋范线性空间按照标准凸结构W(x,y,λ)=λx+(1-λ)y(∀x,y∈X,∀0≤λ≤1)构成凸度量空间,W-凸集就是通常意义下的凸集。由于凸度量空间不一定具有线性结构,不一定是线性空间,所以W-凸集不一定是通常意义下的凸集。
现在引进凸度量空间中的3种广义凸函数,为方便读者,将已有3种一并列出。
定义3设(X,d,W)是凸度量空间,K⊆X是W-凸集,f:K→R。
(1) 如果∀x,y∈K,∀λ∈[0,1],都有
f(W(x,y,λ))≤λf(x)+(1-λ)f(y)
称f(x)为K上的W-凸函数[5]。
(2) 如果∀x,y∈K,x≠y,∀λ∈(0,1),都有
f(W(x,y,λ))<λf(x)+(1-λ)f(y)
称f(x)为K上的W-严格凸函数[5]。
(3) 如果∀x,y∈K,f(x)≠f(y),∀λ∈(0,1),都有
f(W(x,y,λ))<λf(x)+(1-λ)f(y)
称f(x)为K上的W-半严格凸函数。
(4) 如果∀x,y∈K,∀λ∈[0,1],都有
f(W(x,y,λ))≤max{f(x),f(y)}
称f(x)为K上的W-拟凸函数[6]。
(5) 如果∀x,y∈K,x≠y,∀λ∈(0,1),都有
f(W(x,y,λ)) 称f(x)为K上的W-严格拟凸函数。 (6) 如果∀x,y∈K,f(x)≠f(y),∀λ∈(0,1),都有 f(W(x,y,λ)) 称f(x)为K上的W-半严格拟凸函数。 对于标准凸结构,W-凸函数、W-严格凸函数、W-半严格凸函数、W-拟凸函数、W-严格拟凸函数,W-半严格拟凸函数分别就是通常意义的凸函数,严格凸函数、半严格凸函数、拟凸函数、严格拟凸函数、半严格拟凸函数,后6种函数的定义见文献[1]。 严格W-凸函数既是W-凸的,又是W-半严格凸的和W-严格拟凸的;W-凸函数既是W-拟凸的,又是W-半严格拟凸的;严格W-拟凸函数既是W-拟凸的,又是W-半严格拟凸的;半严格W-凸函数是半严格W-拟凸的。这8种蕴含关系的反蕴含关系,甚至对线性空间中的标准凸结构都不真,反例见文献[1]。 为讨论凸度量空间中的广义凸性,引入条件(W)[10]。 (W)W(W(x,y,t),W(x,y,s),λ)= W(x,y,λt+(1-λ)s) ∀x,y∈X,t,s,λ∈[0,1] 赋范线性空间中的标准凸结构、CAT(0)空间和Busemann空间中的凸结构都满足条件(W)。 取x0=(1,0,0)∈X,令f:X→R为 f(x)=arccosx1,∀x=(x1,x2,x3)∈X 则f是W-凸函数,这是因为 f(W(x,y,λ))=d1(x0,W(x,y,λ))≤λd1(x0,x)+(1-λ)d1(x0,y)=λf(x)+(1-λ)f(y)∀x,y∈X,∀λ∈[0,1] 例2 设X为闭区间族[ai,bi],其中0≤ai W(Ii,Ij,λ)=[λai+(1-λ)aj,λbi+(1-λ)bj] 再通过Hausdorff距离定义X上的度量d,则(X,d,W)是凸度量空间[4]。容易验证凸结构满足条件(W)。令f,g:X→R为f([x,y])=x2+y2,∀[x,y]∈X,有 易知f是W-严格凸函数,g是W-半严格凸函数,从而也是W-半严格拟凸函数,但不是其他4类函数。 引理1[4]设(X,d,W)是凸度量空间,那么∀x,y∈X,λ∈[0,1],有 (1)W(x,x,λ)=x,W(x,y,0)=y W(x,y,1)=x (2)d(x,W(x,y,λ))=(1-λ)d(x,y) d(y,W(x,y,λ))=λd(x,y) 引理2[10]设(X,d,W)是凸度量空间,凸结构W满足条件(W),有 (1)W(x,y,λ)关于λ是连续的; (2) Synchronized性质成立,即 W(x,y,λ)=W(y,x,1-λ) ∀x,y∈X,λ∈[0,1] 除非特别声明,下文总设(X,d,W)是凸度量空间,凸结构W满足条件(W),K⊆X是W-凸集,f:K→R。 引理3 设f为K上的W-半严格拟凸函数,x,y∈K且f(x)=f(y),则 (1) 至多存在一个β∈(0,1),使得 f(W(x,y,β))>f(x)=f(y) (2) 若存在β∈(0,1),使得 f(W(x,y,β))>f(x)=f(y) 则∀λ∈[0,1],λ≠β,有 f(W(x,y,λ))=f(x)=f(y) W(x,y,λ1)=W(W(x,y,λ2),W(x,y,0),λ) 由f为K上W-半严格拟凸函数与引理1,得 f(W(x,y,λ1)) f(W(x,y,λ2)) W(x,y,λ2)=W(y,x,(1-λ2))= W(W(y,x,(1-λ1)),W(y,x,0),1-u) 注意到W(y,x,1-λ1)=W(x,y,λ1),则由f的W-半严格拟凸性,得 f(W(x,y,λ2)) f(W(x,y,λ1)) 这与f(W(x,y,λ1)) (2) 用反证法,由引理3(1)知,f(W(x,y,λ))≤f(x)=f(y),∀λ∈(0,1),λ≠β。假设∃λ0∈(0,1),λ0≠β,使 f(W(x,y,λ0)) W(x,y,β)=W(y,x,(1-β))= W(W(y,x,(1-λ0)),W(y,x,0),1-u) 以及 f(W(x,y,β))< max{f(W(y,x,(1-λ0))),f(x)}=f(x) 与已知条件矛盾。 引理4 若存在α∈(0,1),使∀x,y∈K,f(W(x,y,α))≤αf(x)+(1-α)f(y),则有 (1) 对∀x,y∈K,成立 (2) Λn⊆TW,其中 以及 TW={λ∈[0,1]|f(W(x,y,λ))≤ λf(x)+(1-λ)f(y),∀x,y∈K} 证明(1) 因为 所以由条件(W),对∀x,y∈K,成立 因此由已知条件,得 等价于 α(1-α)f(x)+α(1-α)f(y) 事实上,当0≤m≤2k时,因为 当2k 设(X,d,W)是凸度量空间,K⊆X是W-凸集,f:K→R,如果存在α∈(0,1),使 f(W(x,y,α))≤αf(x)+(1-α)f(y),∀x,y∈K 对线性空间X及其标准凸结构,若f:X→R且f是中间点凸的,那么[0,1]∩Q⊆T,其中T={t∈[0,1]:f(y+t(x-y))≤tf(x)+(1-t)f(y),∀x,y∈X}。下证上述结果对中点W-凸函数也成立。 证明注意到: k=λ1(λ1k)+(1-λ1)[λ2+(1-λ2)k]= 由W满足条件(W),成立 W(x,y,k)= W(W(x,y,λ1k),W(x,y,λ2+(1-λ2)k,λ1) W(x,y,λ1k)= W(W(x,y,k),W(x,y,0),λ1) W(x,y,λ2+(1-λ2)k)= W(W(x,y,1),W(x,y,k),λ2)。 由λ1,λ2∈TW,知 f(W(x,y,k))≤λ1f(W(x,y,λ1k))+ (1-λ1)f(W(x,y,(λ2+(1-λ2)k)))≤ λ1[λ1f(W(x,y,k))+(1-λ1)f(y)]+ (1-λ1)[λ2f(x)+(1-λ2)f(W(x,y,k))]= (1-λ1)λ2f(x)+(1-λ1)(1-λ2)f(W(x,y,k)) 因此,得到 λ1(1-λ1)f(y)+(1-λ1)λ2f(x) 即有 证明由引理4,知 现在讨论稠密性定理在优化问题中的应用。 证明设x0∈K是f的局部极小值点,则∃ε>0,∀x∈Bε(x0)∩K,f(x0)≤f(x)。任取y∈K,由于K是W-凸集,知∀λ∈(0,1),W(x0,y,λ)∈K。由稠密性定理得[0,1]∩Q⊆TW。取充分接近1的有理数λ0∈[0,1]∩Q⊆TW,使 d(x0,W(x0,y,λ0))≤λ0d(x0,x0)+ (1-λ0)d(x0,y)=(1-λ0)d(x0,y)<ε 则W(x0,y,λ0)∈Bε(x0)∩K,从而 f(x0)≤f(W(x0,y,λ0))≤ λ0f(x0)+(1-λ0)f(y) 进而f(x0)≤f(y)。由y的任意性,知x0是f的全局极小值点。 设(X,d,W)是凸度量空间,W满足条件(W),K⊆X是W-凸集,考虑多目标规划问题(MP): (MP) minF(x)=(f1(x),…,fm(x))T,x∈K 其中,fi:K→R1(i=1,2,…,m),F:K→Rm是向量值函数。记 TWi={t∈[0,1]|fi(W(x,y,t))≤tfi(x)+ (1-t)fi(y),∀x,y∈K},i=1,2,…,m 证明由稠密性定理得[0,1]∩Q⊆TWi。设x0∈K为问题(MP)的局部有效解,即存在x0的邻域Bε(x0),不存在x∈Bε(x0)∩K,使得fi(x)≤fi(x0),i=1,2,…,m,至少存在一个1≤j≤m,使fj(x) 若x0∈K不是全局有效解,那么∃x*∈K,使fi(x*)≤fi(x0),i=1,2,…,m,至少存在1≤j≤m,使fj(x*) d(x0,W(x0,x*,λ))≤ λd(x0,x0) +(1-λ)d(x0,x*)<ε 则W(x0,x*,λ)∈Bε(x0)∩K,从而 fi(W(x0,x*,λ))≤ λfi(x0)+(1-λ)fi(x*)≤fi(x0) i=1,2,…,m,且 fj(W(x0,x*,λ))≤ λfj(x0)+(1-λ)fj(x*) 矛盾,故定理得证。 本节讨论W-凸函数的一些判别准则。设(X,d,W)是凸度量空间,W满足条件(W),K⊆X是W-凸集,f:K→R。 证明∀x,y∈K,∀λ∈[0,1],由定理1,TW在[0,1]中是稠密的,因此存在收敛于λ的序列{λn}⊆TW。由引理2,W(x,y,t)关于t连续且f下半连续,则有 λf(x)+(1-λ)f(y) 这说明f是W-凸函数。 证明∀x,y∈K,∀λ∈[0,1],只需证明f(W(x,y,λ))≤λf(x)+(1-λ)f(y)。 不妨λ≠0,λ≠1,x≠y。由TW在[0,1]中稠密,取λn∈TW,λn>λ,使λn→λ,则 f(W(x,y,λ))= f(W(x,y,λ))≤λf(x)+(1-λ)f(y) 证明∀x,y∈K,∀t∈(0,1),只需证明f(W(x,y,t))≤tf(x)+(1-t)f(y)。 (1) 当f(x)=f(y)时,由f的W-拟凸性得到 f(W(x,y,t))≤max{f(x),f(y)}= f(x)=tf(x)+(1-t)f(y) (2) 当f(x)≠f(y)时,有 ① 若f(y) 1) 当∃t f(W(x,y,t))= max{f(W(x,y,t′)),f(y)}=f(y)< tf(x)+(1-t)f(y) f(W(x,y,t))≤ max{f(W(x,y,0)),f(W(x,y,tn))}= f(W(x,y,tn))≤tnf(x)+(1-tn)f(y) n→∞,得 f(W(x,y,t))≤tf(x)+(1-t)f(y) ② 若f(x) f(W(x,y,t))≤max{f(W(x,y,t′)),f(x)}=f(x)≤ tf(x)+(1-t)f(y) W(x,y,t)=W(W(x,y,1),W(x,y,tn),αn) f(W(x,y,t))≤max{f(x),f(W(x,y,tn))}= f(W(x,y,tn))≤tnf(x)+(1-tn)f(y) 令n→∞,有 f(W(x,y,t))≤tf(x)+(1-t)f(y) 证明W-半严格凸函数是W-半严格拟凸函数,因此不妨设f是W-半严格拟凸函数。由定理6,现只需证明f为W-拟凸函数。 如果f不是W-拟凸函数,那么 ∃x,y∈K,x≠y,∃λ0∈(0,1) f(W(x,y,λ0))>max{f(x),f(y)} (1) 当f(x)≠f(y)时,由f的W-半严格拟凸性,有 f(W(x,y,λ0)) 矛盾。 (2) 当f(x)=f(y)时,由引理3,f(W(x,y,λ))=f(x)=f(y),∀λ∈[0,1],λ≠λ0, f(W(x,y,λ0))= 矛盾。以上说明f为W-拟凸函数,从而由定理6知结论成立。 针对凸度量空间中的抽象凸结构,将线性空间中基于标准凸结构的3种广义凸函数概念引入了凸度量空间,定义了3种新广义W-凸函数,证明了中间点W-凸函数是中点W-凸的以及[0,1]∩Q-W-凸的,获得了稠密性定理;利用中点W-凸性,建立了W-凸函数的判别准则等。获得稠密性定理的方法有一定的技巧性与新意,可以应用于一些其他凸或广义凸映射稠密性问题的研究,例如对中间点预不变凸函数的相关稠密性问题的研究。利用中点广义凸性而不是中间点广义凸性建立判别准则的方法,可以应用于建立其他一些凸或广义凸或锥凸或广义锥凸映射的判别准则。例如,利用本文及文献[1]中的思想方法,可以作如下乐观的预期:一方面,可以将文献[1]中建立凸函数判别准则的条件中间点凸性简化为中点凸性;另一方面,可以将文献[1]中严格凸函数、拟凸函数等的一些判别准则相应推广到凸度量空间。

2 中点W-凸性与稠密性定理







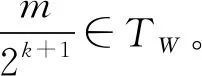

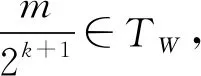
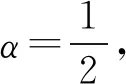

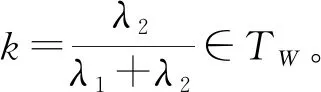
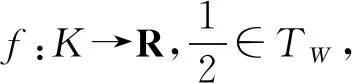
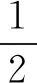
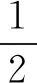
3 W-凸函数判别准则
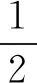



4 结 论

