广义集值映射Nash均衡点的存在性及Levitin-Polyak良定性*
刘 雷,林 志,彭再云,王衍程
(重庆交通大学 数学与统计学院,重庆 400074)
0 引 言
一般认为,1944年Morgenstern等[1]书的出版,标志着系统化对策论的出现,他们主要研究了矩阵对策与合作对策。此后,在1950年[2]与1951年[3],Nash在其基础上相继发表了关于非合作对策的两篇重要文章,引入了非合作对策均衡点的概念(即Nash均衡点),从而完善了现代非合作对策理论。其中,很多学者围绕Nash均衡点的存在性问题进行了大量研究,也取得了很多成果。经典对策问题的支付映射是单值的(一个数或一个向量)[4-6],然而,受客观条件和一些不确定因素的影响,要精确计算出其对应值很困难,甚至不可能,通常只能得到这个值的大概范围。此时,相应对策问题的支付映射就变成了一个集值映射。因此,研究带有集值支付映射的对策问题是非常必要且有实际意义的。
在此背景下,文献[7]在支付映射为集值的条件下,讨论了对策系统的Loose Nash均衡点的存在性;文献[8]在Loose Nash均衡点的基础上,重新刻画了支付映射为集值时对策系统Nash均衡点的定义,并证明了其存在性,但是其均不带约束条件,实际应用时具有一定的局限性,且均未讨论其均衡点的稳定性。
良定性(Well-posedness)是稳定性理论和数值分析中的一个重要概念。1966年,Tykhonov[9]在近似解序列的基础上提出了无约束优化问题良定性的概念;在同一年,Levitin等[10]将Tykhonov定义的良定性推广到了带约束的优化问题中,人们分别称其为Tykhonov良定性和Levitin-Polyak良定性(简称为LP良定性)。近年来,有关带约束优化问题的LP良定性的研究愈加热门[11-14],但尚未有关于集值映射Nash均衡点的良定性分析。
本文将文献[8]中无约束集值映射的Nash均衡点,推广到了带约束的广义集值映射Nash均衡点,并证明了其存在性。它以通常的Nash均衡点[4-6]及集值映射的Loose Nash均衡点[7]为特例,应用更加广泛。此外,通过定义LP近似解序列,证明了LP良定性的充分和必要条件,并在此基础上,得到了广义集值映射Nash均衡点的LP良定性结果。
1 预备知识
定义1 设Y是Hausdorff拓扑线性空间,C⊂Y是Y中的一个锥,C为凸锥,当且仅当C+C=C;C为尖锥,当且仅当C∩C={θ},其中θ是Y中的零元。
定义2设Y是Hausdorff拓扑线性空间,对集合A,B⊂Y,数α∈R,记A+B={a+b:a∈A,b∈B},αA={αa:a∈A}。
在本文中,除非特别说明,均定义如下:指标集I={1,2,…,n}至少有两个元素,对任何i∈I,Xi,Yi是Hausdorff拓扑线性空间,Ki是Xi中的一个非空紧凸子集,Ci是Yi中的一个闭凸尖锥且intCi≠∅,记
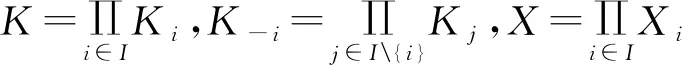
其中,积空间X是一个Tychonoff乘积空间,对每个x∈K,记为x=(xi,x-i)。讨论下面广义集值映射Nash均衡问题:设指标集I是局中人集合,对每个局中人i∈I,集值映射Fi:K→2Yi是局中人i的支付映射,集值映射Gi:K-i→2Ki是其可行约束对应映射,寻找
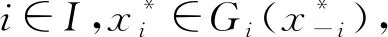
则x*被称为广义集值映射对策系统的一个Nash均衡点。一个广义集值映射的对策系统通常被表示为(SVNGP):Γ={Ki,Gi,Fi}i∈I。

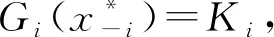
注3 在不带约束的情况下,此定义包含Loose Nash均衡点[7]作为一个特例,具体推论可见文献[8]。同样可证,当文献[8]中的锥Ci(x*)为固定锥时,上述定义中的x*也为文献[8]中的Nash均衡点。
定义3X是一个Hausdorff拓扑空间,Y是一个拓扑向量空间,K是X中的一个非空子集,C是Y中的一个闭凸尖锥,集值映射F:K→2Y。若对Y中零元θ的任何开零域V,存在x在K中的开零域U(x),使得对任何x′∈U(x),有F(x′)⊂F(x)+V+C,则称F在x处是上半C-连续的;若F在K的每一点均是上半C-连续的,则称F在K上是上半C-连续的;若-F在K上是上半C-连续的,则F在K上是上半-C连续的。
定义4[8]X和Y为Hausdorff拓扑线性空间,K是X中的一个非空子集,对任意x∈K,称Fi(·,x-i):Ki→2Yi是Ci-广义拟凹的,如果对任意yi∈2Yi,集合{ui∈Xi:存在zi∈Fi(ui,x-i),zi∈yi+intCi}是凸集。
定义5[15]X和Y是两个拓扑空间,K是X中的一个非空子集,F:K→Y是K到Y的一个集值映射,若对任意x∈K,F(x)恒为Y的紧子集,则称F为紧值映射。
引理1[15]X为拓扑空间,Y为正则拓扑空间,K是X中的一个非空子集,F:K→2Y,若F在x0∈K处上半连续且闭值,则对任意xn→x0,对任意yn∈F(xn)且yn→y0,有y0∈F(x0)。
引理2[15]X和Y为拓扑空间,K是X中的一个非空子集,且Y满足第一可列公理,F:K→2Y,若F在x0∈K处下半连续,则对任意xn→x0,对任意y0∈F(x0),有n0使对任意n≥n0,存在yn∈F(xn)满足yn→y0。
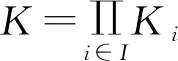
(i)Hi是紧值的;
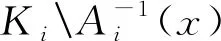
则所有集合Hi(xi)(i∈I,xi∈Ki)有公共元素,即
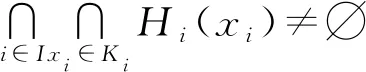
2 存在性及其证明
定理1 设I是局中人的集合,对每个i∈I,Ki是Xi中的非空紧凸子集,集值映射Fi:Ki→2Yi,集值映射Gi:K-i→2Ki。考虑广义集值映射的对策系统Γ,对∀i∈I,如果
(i)∀x-i∈K-i,Gi(x-i)是上半连续的且具非空凸紧值;
(ii)∀x∈K,Fi(·,·)是上半连续的且具非空紧值;
(iii)∀x-i∈K-i,Fi(·,x-i)是Ci-广义拟凹的;
(iv)∀x∈K,Fi(ui,·)是下半连续的;
(v)∀x∈K,存在yi∈Fi(x),使(yi-Fi(x))∩(-intCi)=∅。
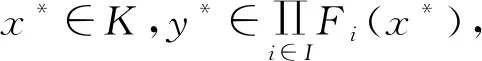

证明对每个i∈I,作映射Hi:Gi(x-i)→2Gi(x-i)如下:
Hi(ui)={xi∈Gi(x-i):存在yi∈Fi(xi,x-i),使(yi-Fi(ui,x-i))∩(-intCi)=∅},∀ui∈Gi(x-i)。
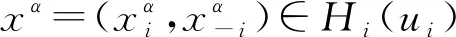
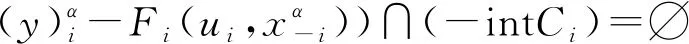
即有
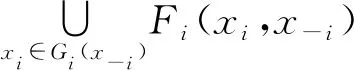

因此x0∈Hi(ui),从而Hi(ui)是闭集当然也是紧集。
(2) 对任意的xi∈Gi(x-i),由条件(iii)有
{ui∈Gi(x-i):xi∉Hi(ui)}=
{ui∈Gi(x-i):∀yi∈Fi(xi,x-i),
∃zi∈Fi(ui,x-i),zi∈yi+intCi}
是凸集。
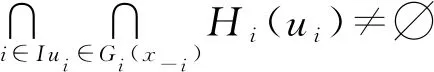

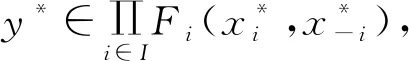
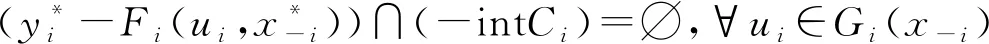
证毕。
注4 当集值映射F简化为向量值函数时,应用上述定理1,依然可得到广义向量对策系统解的存在性结果。
3 良定性及其证明
定义广义集值映射对策系统(SVNGP)的Nash均衡点的解集为S,其中
S={x=(xi,x-i)∈K:∀i∈I,xi∈Gi(x-i)}
且存在yi∈Fi(xi,x-i),使yi-zi∉-intCi,∀zi∈Fi(ui,x-i),∀ui∈Gi(x-i)。
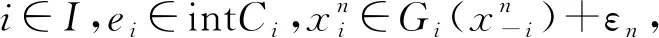

定义7如果存在唯一的(SVNGP)解x*,且每一个近似解序列都收敛到x*,则称(SVNGP)为LP良定的;如果(SVNGP)的解集是一个集合且每一个近似解序列都有收敛子序列收敛到解集中的某点,则称(SVNGP)为广义LP良定的(简称为GLP良定的)。
注5如果(SVNGP)是GLP良定的,那么其解集一定是非空紧值的。
为了刻画良定性问题,下面引入(SVNGP)近似解集的概念:对ε∈R+,(SVNGP)的LP近似解集为
且存在yi∈Fi(xi,x-i),使yi-zi+εei∉-intCi,∀zi∈Fi(ui,x-i),∀ui∈Gi(x-i)。

引理4对每个i∈I,若集值映射Gi:K-i→2Ki在K-i上上半连续且具紧值,序列{εn}⊂R+,{xn}⊂K,使得对每个i∈I,有
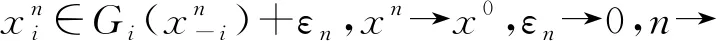
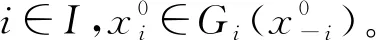
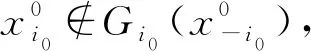
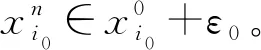
定理2考虑(SVNGP)Γ={Ki,Gi,Fi}i∈I,对每个i∈I,如果
(i)∀x-i∈K-i,Gi(x-i) 是上半连续的且具非空凸紧值;
(ii)∀x∈K,Fi(·,·)是连续的且具有非空紧值;
(iii)∀x-i∈K-i,Fi(·,x-i)是Ci-广义拟凹的;
(iv)∀x∈K,存在yi∈Fi(x),使(yi-Fi(x))∩(-intCi)=∅。
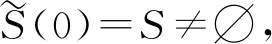
则意味着存在ε0>0,使得
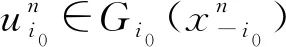

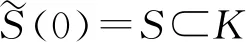
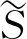
即意味着存在ε0>0,使得
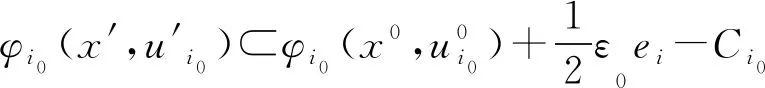

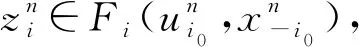
-intCi0-Ci0∈-intCi0

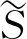
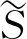
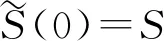
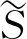
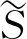
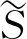
由定理2及定理3,即可得到(SVNGP)的GLP良定性。
定理4对(SVNGP),Γ={Ki,Gi,Fi}i∈I,假设定理2的条件(i)-(iv)全部满足,则(SVNGP)是GLP良定的。
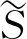
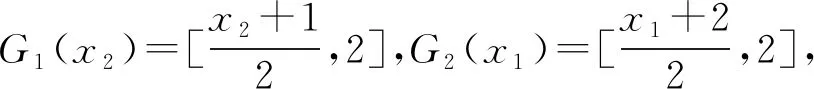
(1)G1(x2),G2(x1)在[1,2]上均是连续且具非空凸紧值;
(2)F1(x1,x2),F2(x1,x2)在[1,2]×[1,2]上均是连续的;
(3) 对任何x2∈[1,2],F1(·,x2)是C1-广义拟凹的,x1∈[1,2],F2(x1,·)是C2-广义拟凹的;
(4) ∀xi∈[1,2],i=1,2,存在0∈Fi(x1,x2),使得(0-Fi(x1,x2))∩(-intCi)=∅。

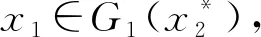
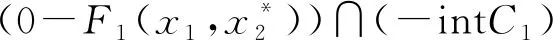
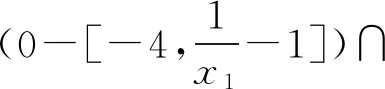
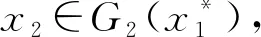
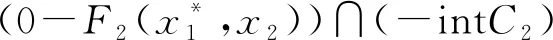
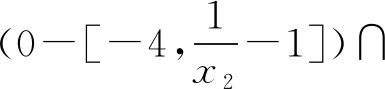
同样定理2的条件均被满足,因此可使用定理4得出上述例子的Nash均衡点是GLP良定的。
注6 当集值映射F简化为向量值函数时,应用上述定理4,依然可得到广义向量对策系统解的良定性结果。
4 结论与讨论
本文讨论了带有约束条件的广义集值映射Nash均衡点的存在性与良定性的相关性质,其在支付映射或者约束对应映射具有非线性扰动或难以精确计算时也可适用。此外,证明了Levitin-Polyak良定性的充分和必要条件,在此基础上,得到了广义集值映射Nash均衡点的Levitin-Polyak良定性结果,得出了大多数情况下广义集值映射Nash均衡点具有良定性的稳定结论,进一步加强了其实际应用价值,丰富了其稳定性的研究内容。接下来,非紧性条件下的广义集值映射Nash均衡点的存在性及其他稳定性将是下一步的研究方向。

