关于累积剩余(r,s)熵的研究*
王甜甜, 汪加梅
(安徽工业大学 数理科学与工程学院,安徽 马鞍山 243032)
0 引 言
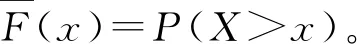

在许多文献中,以不同的方式概括了上式,Havrda等[1]推广了Shannon熵的一种不可加形式:
当r→1时,上面的测度趋于Shannon熵,虽然熵测量Hr(x)最初是由Havrda等在控制论的背景下首次提出的,但Tsallis发现了它的非广延性的特征,并将其放在物理背景下研究,所以熵测度Hr(x)叫做Tsallis熵。1991年,Rathie等[2]引入了统一的(r,s)熵,它包含了许多经典熵,其关于具有概率密度函数f(x)的非负随机变量的形式为
在生命分析和生命测试中,系统的当前年龄也应考虑在内。系统在t时刻仍在运行时的剩余寿命为Xt={X-t|X>t}。1996年,Ebrahimi[3]提出剩余寿命Xt的熵为
2006年,Nanda等[4]提出了Tsallis剩余熵为
2004年,Rao等[5]提出了累积剩余熵的概念,定义为
累积剩余熵(CRE)是基于累积分布函数的一种广义不确定性度量,相比Shannon提出的基于概率密度的测度,该测度具有更稳定的性质。累积剩余熵在连续域和离散域都有一致的定义,它可以很容易地从样本数据中计算出结果且渐进地收敛到真实值。Rao[6],Wang和Vemuri[7]分别在2005年、2007年得出了该测度的若干性质,并在可靠性工程和计算机视觉方面提供了一些应用;2007年,Asadi等[8]考虑了累积剩余熵的动态版本,定义为
已有学者对于累积剩余熵的参数化推广进行了尝试。2010年,Abbasnejad等[9]提出了r阶的动态生存熵(DSE),并解释了其与平均剩余寿命函数的关系。通过考虑CRE与某一部件的平均剩余寿命之间的关系,2015 年,Mohan等[10]在Tsallis熵的基础上提出了累积剩余Tsallis熵及其动态版本:
Mohan刻画了一些著名的寿命分布和概率模型。Kumar[11]在Mohan等的研究基础上继续研究了累积剩余Tsallis熵及其动态版本的性质。但是基于Renyi熵或者是Tsallis熵的累积剩余测度都是不含参数或者仅一个参数。针对前人的研究,将研究基于含有多参数的(r,s)熵定义的累积剩余测度的一些性质与刻画结果。
本篇文章的结构如下:第一节中提出了累积剩余(r,s)熵,同时给出了一些特定分布的表达式;第二部分提出了动态剩余(r,s)熵,研究了其性质刻画;第三部分中,利用平均剩余寿命函数和风险率函数与累积剩余(r,s)熵的关系来刻画一些特定分布的性质。
1 累积剩余(r,s)熵
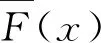
r>0,r≠1,s>0
(1)
下面的引理给出了累积剩余(r,s)熵有界的充分条件:
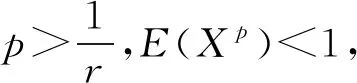
证明令X∈L1,则有E(x)<1,可以得到:
以下是非负随机变量的一些不同单变量连续分布的测度表达。
推论1 (1)X服从参数为b>0的有限维分布,则

(2) 若X在(a,b),a (3) 若X服从参数a>1的Pareto分布,则 (4) 若X服从参数λ>0的指数分布,则 2015年,Mohan等[10]给出了动态累积剩余Tsallis熵测度的定义,相应地,下面定义了动态累积剩余(r,s)熵测度: r>0,r≠1,s>0 (2) X的平均剩余寿命定义为 引理2 当t>0,s>0,r>1(0 证毕。 证明由式(2)得: (3) 对式(3)关于t微分,有 即有 (4) 在这一节中,利用平均剩余寿命函数和风险率函数来刻画一些分布。平均剩余寿命和风险率函数的关系为 (5) 其中,λF(t)为风险率函数。 在给出定性结果前,先来证明下面的定理。 (6) 则有 证明充分性:若非负随机变量X服从指数分布,其概率密度函数、生存函数、平均剩余寿命分别是 f(t)=λe-λt,λ>0,t>0 因此,由定义式(2),有 若非负随机变量X服从Pareto分布,其概率密度函数、生存函数、平均剩余寿命分别是 因此根据定义式(2),简化为 这里若r>1,则 若非负随机变量X服从有限维分布,其概率密度函数、生存函数、平均剩余寿命分别是 f(t)=b(1-t)b-1,b>0,0 因此,经过简化得 这里若r>1,则 必要性:令式(6)成立,根据式(2)有 (7) 式(7)左右两边对t微分,得到 根据平均剩余寿命和风险率之间的关系: λF(t)δF(t) = 1 +δF′(t) (8) 则有 (9) 将式(9)两边同时对t在(0,x)上积分,得到 接下来,将结果推广到一个更一般的情形,将k作为t的函数。 定理3 若X是非负连续随机变量,满足 (10) 那么 证明由式(2),有 代入式(10),得 也即 (11) 两边同时对t微分,得 代入式(5)和式(11),得 k′(t)δF(t) +sk(t)δF′(t) (12) 简化式(12),得 解这个非齐次线性微分方程,有 即证。 接下来,用风险率函数来描述动态累积剩余(r,s)熵的寿命模型,有以下结果。 (13) 那么 证明假设式(13)成立,那么有 由此可得 (14) 式(14)可转化为 等式两边同时对t微分,得 (9) 定理的唯一性易证。 将累积剩余熵推广到参数更多的(r,s)熵,定义了其相关的累积剩余熵及其动态版本,并研究了这些广义信息测度的一些性质和刻画结果。值得注意的是,当r≠1,s=1时,可由累积剩余(r,s)熵得到累积剩余Tsallis熵;当r≠1,s=0时,可由累积剩余(r,s)熵得到累积剩余Renyi熵。根据r和s的其他不同取值也可得到相应的基于其他熵的累积剩余熵,即累积剩余(r,s)熵涵盖了其他多种基于单参数熵定义的累积剩余熵,具有重要参考意义。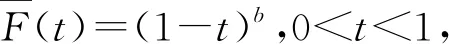
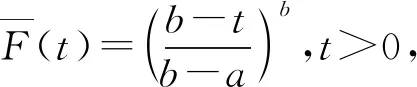
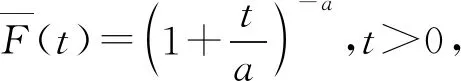
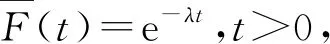
2 动态累积剩余(r,s)熵
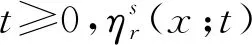

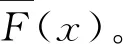
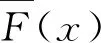

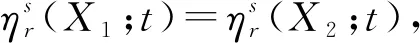
3 特定寿命分布的特征结果
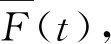
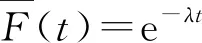
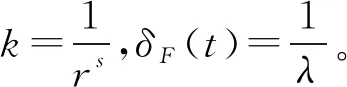
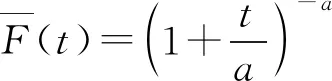

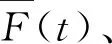

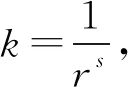
4 结 论

