布尔代数的犹豫模糊点子代数

姜曼

(西安交通工程学院公共课部, 陕西 西安 710300)

0 引言

美国科学家Zadeh在1965年提出了模糊集[1]，自然界中很多事物的表述并不是绝对的，恰恰相反，我们遇到的大多数问题是模糊的，解决方法也并不是唯一的，也是模糊的.因此模糊集的提出对认识自然有很重要的意义.模糊集已经应用到很多方面,现阶段,学者们主要研究的是模糊集以及由模糊集得到的拓展—直觉模糊集[2]、区间值模糊集[3]、双极值模糊集[4]、犹豫模糊集[5]等理论.然而仅研究模糊集及其拓展，对模糊集的认识并不深刻,因此我们把模糊集及其拓展和代数结构相结合，由于不同代数结构的性质不同，因此这种结合方法就很有意义.现阶段，对于布尔代数的子代数的研究也有很多结论，比如，王丰效[6]把布尔代数与模糊集相结合，给出了(λ,μ)模糊子代数的概念并讨论其性质；张瑜[7]等给出了布尔代数的Superior子代数的定义研究它的等价刻画，更多关于布尔代数研究的结论可见文献[8-10].本研究把犹豫模糊集和布尔代数相结合，研究布尔代数上的犹豫模糊点子代数以及它的基本性质，证明了布尔代数的犹豫模糊点子代数的交，同态像及同态逆像的不变性.

1 预备知识

定义1.1[11]具有两个二元代数运算+，·的代数系统〈R;+,·,0,1〉称为布尔代数，如果R至少含有两个不同元，且∀a,b，c∈R，下面公理成立：

1) 交换律a+b=b+a,ab=ba，其中ab为a·b；

2) 分配律a(b+c)=ab+ac，a+(bc)=(a+b)(a+c)；

3) 结合律 (a+b)+c=a+(b+c)，(ab)c=a(bc)；

4) 0-1律 ∃0，1∈R,a+0=a，a1=a；

布尔代数〈R;+,·,0,1〉也记为〈R;+,·,-,0,1〉.

若无特殊说明，布尔代数〈R;+,·,-,0,1〉简记为R，布尔代数〈R′;+,·,-,0′,1′〉简记为R′.

定理1.1[11]设〈R;+,·,0,1〉为布尔代数，∀a,b∈R，有：

1)a0=0，a+1=1，aa=a，a+a=a；

定理1.2[11]布尔代数R与R′的直积R×R′仍为布尔代数.

定义1.3[11]设映射f:R→R′称为从代数系统R到R′的同态映射，如果f保持代数系统的所有代数运算，即映射f满足下列条件：

1)∀a,b∈R，f(a+b)=f(a)+f(b)；

2)∀a,b∈R，f(ab)=f(a)f(b)；

说明：上述定义1.1～1.3和定理1.1～1.2，在文献[11]中的第三章，本章系统介绍了布尔代数的定义与基本性质，子代数、直积，同态与同构定理.

定义1.4[10]设μ:R→[0,1]是R的模糊子集，如果对∀a,b∈R，下面条件成立：

则称μ是R的模糊子代数.

定义1.5[5]设X是一个非空经典集合，一个X上的犹豫模糊集F的定义如下：

F:{(x,hF(x))|x∈X},

其中hF(x)是由区间[0,1]上若干个不同值构成的集合，表示X中的元素x属于集合F的若干种可能隶属度.

设F为X中的犹豫模糊集，P([0,1])为区间[0,1]的幂集，称集合

X(F,γ):={x∈X|γ⊆hF(x)}

为F的犹豫水平集，其中γ⊆P([0,1]).记X中的犹豫模糊集为HF(X).

定义1.6[5]对于F∈HF[X]，犹豫模糊元hF(x)的下界和上界分别定义如下：

下界:hF-(x)=minhF(x),上界:hF+(x)=maxhF(x).

犹豫模糊集的三个基本运算补、并和交分别定义如下：

1) 补：对于F∈HF[X]，它的补元Fc定义为：

补运算满足对合律，即(Fc)c=F.

2) 并：F,G∈HF[X]，F和G的并F∪G定义为：∀x∈X，

hF∪G(x)=hF(x)∪hG(x)={h∈hF(x)∪hG(x)|h≥max(hF-(x),hG-(x))}.

3) 交：F和G的交F∩G定义为：

hF∩G(x)=hF(x)∩hG(x)={h∈hF(x)∩hG(x)|h≤min(hF+(x),hG+(x))}.

定义1.7[12]设X和Y是两个集合，f：X→Y是X到Y的映射，A:={(x,hA(x))|x∈X}和B:={(y,hB(y))|y∈Y}是两个分别定义在X，Y的犹豫模糊子集，x∈X，y∈Y，定义：

且hf-1(B)(x)=hB(f(x))，则f(A)，f-1(B)分别是X和Y的犹豫模糊集，称f(A)为A的像，f-1(B)为B的原像.

2 主要结论

本文中若无特殊说明，均用R表示布尔代数.

定义2.1设μ:R→P([0,1])∈HF[R]，如果对∀a,b∈R，下面条件成立：

1)hμ(a+b)⊇hμ(a)∩hμ(b)，

2)hμ(ab)⊇hμ(a)∩hμ(b)，

则称μ是R的犹豫模糊子代数.记R上的犹豫模糊子代数的全体为HFS[R].

定义2.2设μ:R→P([0,1])∈HF[R]，若对∀a,b∈R，下面条件成立：

1)hμ(a+b)⊇hμ(a)hμ(b)，

2)hμ(ab)⊇hμ(a)hμ(b)，

则称μ是R的犹豫模糊点子代数.记R上的犹豫模糊点子代数的全体为HFDS[R].

定理2.1如果μ∈HFS[R]，则μ∈HFDS[R].

定理2.1的证明设μ∈HFS[R]，对∀a,b∈R则有：

hμ(a+b)⊇hμ(a)∩hμ(b)⊇hμ(a)hμ(b)，hμ(ab)⊇hμ(a)∩hμ(b)⊇hμ(a)hμ(b).

因此，μ∈HFDS[R].

根据定理2.1可得，布尔代数的犹豫模糊点子代数是布尔代数的犹豫模糊子代数的拓展.我们可以简化定义2.1中的条件，这样可以方便后面的证明.

定理2.2设μ∈HF[R]，则μ∈HFDS[R]当且仅当定义2.2中的条件1)和3)成立.

定理2.2的证明(1)必要性，易证.

(2)充分性.现在我们需要证明定义2.2中的条件2)成立.对∀a,b∈R有：

因此定义2.2中2)成立.

定理2.3设μ∈HF[R]，则μ∈HFDS[R]当且仅当定义2.2中的条件2)和3)成立.

定理2.3的证明(1)必要性.易证.

(2)充分性.现在我们需要证明定义2.2中的条件1)成立.对∀a,b∈R有：

因此定义2.2中1)成立.

定理2.4设μ∈HFDS[R]，则对∀a∈R，下列结论成立：

2)[hμ(a)]2⊆hμ(0).

定理2.5设μ∈HFDS[R]，则U={a∈R|hμ(a)=1}≠∅是R的子代数.

定理2.6设μ∈HFDS[R]，ν∈HFDS[R]，则μ∩ν∈HFDS[R].

定理2.6的证明∀a,b∈R，则

hμ∩ν(a+b)=hμ(a+b)∩hν(a+b)

⊇(hμ(a)hμ(b))∩(hν(a)hν(b))

⊇(hμ(a)∩hν(a))(hμ(b)∩hν(b))

=hμ∩ν(a)hμ∩ν(b),

所以，μ∩ν∈HFDS[R].

推论2.1的证明同定理2.6,故省略.

定理2.7设f:R→R′是同态满射，若ν∈HF[R′]，则ν∈HFDS[R′]当且仅当f-1(ν)∈HFDS[R]，并且hf-1(ν)(a)=hν(f(a))，∀a∈R.

定理2.7的证明1)必要性.因为ν∈HFDS[R′]，所以对∀a,b∈R，有

hf-1(ν)(ab)=hν(f(ab))=hν(f(a)f(b))⊇hν(f(a))hν(f(b))=hf-1(ν)(a)hf-1(ν)(b).

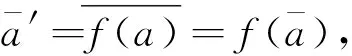
因此，f-1(ν)∈HFDS[R].

2)充分性.已知f-1(ν)∈HFDS[R].

对∀a′,b′∈R′，由于f:R→R′是同态满射，所以∃a,b∈R，有f(a)=a′，f(b)=b′.因此

hν(a′b′)=hν(f(a)f(b))=hν(f(ab))=hf-1(ν)(ab)

⊇hf-1(ν)(a)hf-1(ν)(b)

=hν(f(a))hν(f(b))=hν(a′)hν(b′)

所以，ν∈HFDS[R′].

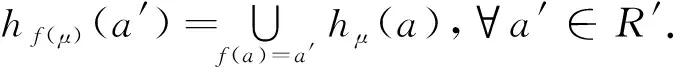
定理2.8的证明因为f:R→R′是同态满射，所以∀a′,b′∈R′，∃a,b∈R，使得f(a)=a′，f(b)=b′.因此：

=hf(μ)(a′)hf(μ)(b′)，

所以，f(μ)∈HFDS[R′].

定理2.9设δ∈HF[R]，μδ∈HF[R×R]，并且hμδ(a,b)=hδ(a)hδ(b)，∀a,b∈R，则δ∈HFDS[R]当且仅当μδ∈HFDS[R×R].

hμδ[(a,a′)+(b,b′)]=hμδ(a+b,a′+b′)=hδ(a+b)hδ(a′+b′)

⊇[hδ(a)hδ(b)][hδ(a′)hδ(b′)]=[hδ(a)hδ(a′)][hδ(b)hδ(b′)]

=hμδ(a,a′)hμδ(b,b′)，

故μδ∈HF[R×R].

2)充分性.已知μδ∈HF[R×R]，于是∀a,b∈R，有

[hδ(a+b)]2=hδ(a+b)hδ(a+b)=hμδ(a+b,a+b)=hμδ[(a,b)+(b,a)]

⊇hμδ(a,b)hμδ(b,a)=[hδ(a)hδ(b)][hδ(b)hδ(a)]

=[hδ(a)hδ(b)]2.

因此hδ(a+b)⊇hδ(a)hδ(b).

于是，δ∈HFDS[R].

定理2.10设μ∈HFDS[R],ν∈HFDS[R′]，则μ×ν∈HFDS[R×R′]，其中对∀(a,a′)∈R×R′，hμ×ν(a,a′)=hμ(a)hν(a′).

定理2.10的证明∀(a,a′),(b,b′)∈R×R′，则有：

hμ×ν[(a,a′)+(b,b′)]=hμ×ν(a+b,a′+b′)

=hμ(a+b)hν(a′+b′)

⊇[hμ(a)hμ(b)][hν(a′)hν(b′)]

=[hμ(a)hν(a′)][hμ(b)hν(b′)]

=hμ×ν(a,a′)hμ×ν(b,b′),

故μ×ν∈HFDS[R×R′].