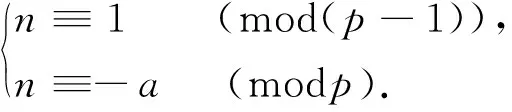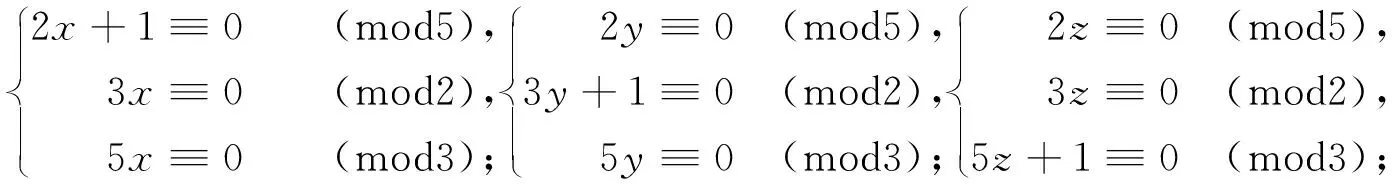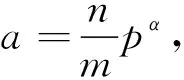数学基础课里的中国剩余定理
刘合国,赵静
(湖北大学数学与统计学学院,湖北 武汉 430062)
0 引言
中国剩余定理蕴含了一种自然有效的数学思想,在理论和应用等方面都具有基本性和重要性. 现在,我们要从模的完全剩余系,以及整系数线性方程组这两个角度来分别推导这个定理,并给出中国剩余定理的两种自然解法. 同时我们也给出中国剩余定理在初等数论、多项式代数、矩阵代数等方面的一些应用,由此我们可以体会到中国剩余定理在大学数学的基础课教学中的重要性.
本研究是文献[1]的续篇,涉及的矩阵代数、数论等方面的知识见献[2-4].
1 从完全剩余系的角度出发
我们从一个简单的观察入手.
设m1,m2,…,mn是n个正整数.对每个整数0≤a a=rnm1m2…mn-1+qn, 其中0≤rn 同样地,qn可唯一地表示为 qn=rn-1m1m2…mn-2+qn-1, 其中0≤rn-1 继续下去,a可唯一地表示为 a=r1+r2m1+r3m1m2+…+rnm1m2…mn-1, 其中0≤ri 这样,我们就证明了下面的定理. 定理1.1设m1,m2,…,mn是n个正整数,Ri={0,1,…,mi-1}是模mi的完全剩余系.则 r1+r2m1+r3m1m2+…+rnm1m2…mn-1 是模m1m2…mn的完全剩余系,这里ri∈Ri,1≤i≤n. 根据定理1.1,我们能够得到中国剩余定理的一种解法. 定理1.2(中国剩余定理) 设m1,m2,…,mn是两两互素的正整数.对任意整数a1,a2,…,an,下列方程组 在模m1m2…mn下有唯一解. 定理1.2的证明对n进行归纳.当n=1时,解是自明的.当n=2时,即求解 (1) 因m1与m2互素,故关于y的同余方程a1+m1y≡a2(modm2)有唯一解y.我们不难验证x≡a1+m1y(modm1m2)是方程组(1)的解.归纳假设,z是 的解.因m1m2…mn-1与mn互素,故关于t的同余方程z+tm1m2…mn-1≡an(modmn)有唯一解t.不难验证x≡z+tm1m2…mn-1(modm1m2…mn)是题中方程组的解. 解的唯一性可以直接验证,在此略去. 上面的证明给出了求解中国剩余定理的一种方法:依次解出x1,x2,…,xn,使 最后,x≡x1+x2m1+x3m1m2+…+xnm1m2…mn-1(modm1m2…mn)就是所求的解. 下面的例子来自陈志坚编撰的《求一得斋算学》. 例1.3求解 解依次求解 解得 x1=2,x2=2,x3=1,x4=12. 因此,x=2+3·2+15·1+105·12=1 283. 下面的例子来自黄宗宪《求一术通解》卷上. 例1.4今有物不知总,以五累减之无剩,以七百一十五累减之剩一十,以二百四十七累减之剩一百四十,以三百九十一累减之剩二百四十五,以一百八十七累减之剩一百零九.问总数若干? 解用数学语言翻译这一问题,即是求解 该方程组等价于 依次求解 解得 x1=0,x2=3,x3=10,x4=7,x5=0,x6=0. 因此,x=15+5×23×10+5×23×11×7=10 020. 上面的思想可以拓展到域F上的一元多项式的情况.我们可以证明如下的两个定理. 定理1.5设m1(x),m2(x),…,mn(x)是域F上的n个非零多项式.F[x]的每个次数小于∂(m1(x)m2(x)…mn(x))的多项式f(x)可唯一地表示为 f(x)=r1(x)+r2(x)m1(x)+r3(x)m1(x)m2(x)+…+rn(x)m1(x)m2(x)…mn-1(x), 其中∂(ri(x))<∂(mi(x)),1≤i≤n. 定理1.6(F[x]上的中国剩余定理) 设m1(x),m2(x),…,mn(x)是F[x]的两两互素的多项式.对任意多项式r1(x),r2(x),…,rn(x),存在唯一次数小于∂(m1(x)m2(x)…mn(x))的多项式f(x),使 f(x)≡ri(x) (modmi(x)), 其中1≤i≤n. 例1.7设f(x)是2n-1次多项式,其中n是正整数.若f(x)+1被(x-1)n整除,f(x)-1被(x+1)n整除,求f(x). 解注意到恒等式 =(x+1)n·u(x)+(x-1)n·v(x), 所求问题等价于求解 取r1(x)=-1,再求次数 (-1)+(x-1)n·r2(x)≡1 (mod(x+1)n). 这样取r2(x)=2v(x)即可.此时, f(x)=(-1)+(x-1)n·r2(x) =2(x-1)nv(x)-1 在本节我们将从整线性方程组AX=b的角度来考察中国剩余定理, 由此给出一种矩阵解法. 设M是n阶整数矩阵. 存在整数矩阵L, 使得ML=In的充要条件是M的行列式等于±1. 我们把行列式等于±1的矩阵称为模矩阵. 对任意一个整数矩阵,进行如下的三种初等变换: 1) 互换矩阵的两行(列), 2) 矩阵的某一行(列)乘以-1, 3) 把矩阵某一行(列)的整数倍数加到另一行(列). 我们把这三种初等变换称为模变换,它们对应的初等矩阵都是模矩阵. 按照文献[4],对于任意的m×n整数矩阵A,它在模变换下可以变为如下的标准形式 其中di(1≤i≤r)是正整数,d1|d2|…|dr.这也意味着,存在m阶模矩阵P和n阶模矩阵Q,使 称(d1,d2,…,dr)为A的不变量. 定理2.1整系数线性方程组AX=b有整数解的充要条件是系数矩阵A和增广矩阵(A,b)具有相同的不变量. 下面我们给出整系数线性方程组AX=b的一种矩阵解法,同时定理2.1的证明也可从该解法中直接导出. 设A是m×n矩阵,(d1,d2,…,dr)是A的不变量.则存在m阶模矩阵P和n阶模矩阵Q,使 于是Ax=b变为P-1JQ-1X=b,即J(Q-1X)=Pb.记 由此AX=b进一步演变为下面的简单形式 (2) 整线性方程组(2)有整数解当且仅当cr+1=…=cm=0,且di|ci(1≤i≤r). (1) 对(A,b)进行行的模变换; Χ可变为 AX=b有整数解当且仅当cr+1=…=cm=0,di|ci(1≤i≤r),此时系数矩阵A和增广矩阵(A,b)具有相同的不变量.当AX=b有整数解时,其解为 其中,yr+1,…,yn是任意整数. 例2.2解整系数线性方程组 解构造矩阵 对X的前3行进行行的模变换,前4列进行列的模变换,Χ可变为 于是方程组的整数解为 其中k1,k2是任意整数. 再回到中国剩余定理. 定理1.2的另一个证明只需证明解的存在性.明显地,求解同余方程组 等价于解下面的整线性方程组 (3) 整线性方程组(3)的系数矩阵为 当m1,m2,…,mn两两互素时,其在模变换下的标准形为 这样对任意整数a1,a2,…,an,整线性方程组(3)的增广矩阵 的标准形为 显然A和B具有相同的不变量. 因此,该整线性方程组(3)总有整数解. 下面的例子即《张邱建算经》里著名的“百钱买百鸡”问题,该书编写于公元五世纪. 例2.3今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一. 凡百钱,买百鸡,问鸡翁、母、雏各几何? 解用数学语言翻译这个问题.即设鸡翁、母、雏的数目分别为x,y,z.则 构造矩阵 对Χ的前2行进行行的模变换,前3列进行列的模变换,Χ可变为 于是方程组的一般形式解为 因此,所求的解为 例3.1解x3≡ 53 (mod120). 解原方程等价于同余方程组 (4) 根据Fermat小定理和推广的Euler定理可得,同余方程组(4)等价于下面的方程组 (5) 按照文献[1]中的解法,方程组(5)等价于 将第一个方程减去第二个方程再减去第三个方程可得x≡77 (mod120). 例3.2解方程组 解由x2+2x≡3 (mod5),知(x,5)=1.根据Fermat小定理可得x4≡1 (mod5).这意味着 x2≡1 (mod5), 或x2≡-1 (mod5). 于是x2+2x≡3 (mod5)等价于 1+2x≡3 (mod5), 或 -1+2x≡3 (mod5), 即 x≡1 (mod5), 或x≡2 (mod5). 又 7x≡3 (mod11)等价于21x≡9 (mod11), 即 x≡2(mod11). 这样原方程等价于 解得x≡46 (mod55)或x≡2 (mod55). 例3.3求x2≡1 (modm)的解的个数. 解设m=2αp1α1p2α2…psαs是m的标准分解,则x2≡1 (modm)等价于如下的同余方程组 (6) 注意到 x2≡1 (mod2α)等价于下列形式之一: (ⅰ)x≡1 (mod2α),当α=1时; (ⅱ)x≡±1 (mod2α), 当α=2时; (ⅲ)x≡±1 (mod2α), 或x≡±1 (mod2α-1), 当α≥3时. 对每个奇素数pi,x2≡1 (modpiαi)等价于x≡±1 (modpiαi). 因此,同余方程组(6)等价于 (7) 其中aj∈{±1},0≤j≤s,β=α或α-1.根据中国剩余定理可得同余方程组(7)存在唯一解. 这样x2≡1 (modm)的解数为 其中α≤2,p是奇素数. 例3.4证明:对每个正整数n,存在n个连续正整数,其中每个都不能表示为两个自然数的平方之和. 例3.4的证明形如4k+3的素数有无穷多个,现任取n个形如4k+3的素数p1,p2,…,pn.运用中国剩余定理,下面的同余方程组 有正整数解x0. 1≡xpi-1≡xpi-3·x2≡ypi-3·(-y2)≡-ypi-1≡-1 (modpi), 矛盾.因此a1,a2,…,an都不能表示为两个素数的平方之和. 例4.1设f(x)是一个整系数多项式, 对每个正整数m, 记 Nm=|{x∈Z|f(x)≡0 (modm)}|, 证明当m1,m2,…,ms两两互素时,Nm1m2…ms=Nm1·Nm2·…·Nms. 例4.1的证明只需对s=2进行证明即可. 记m=m1m2,S={0≤x Si={0≤x 下证在S与S1×S2之间存在一个自然的一一对应. 任取x∈S, 即0≤x 反过来, 任取(y1,y2)∈S1×S2, 即m1|f(y1),m2|f(y2).根据中国剩余定理, 存在唯一的整数0≤y 因mi|y-yi,y-yi|f(y)-f(yi), 故mi|f(y),m1m2|f(y), 即m|f(y).因此,y∈S.这就证明了 Nm1m2=|S|=|S1×S2|=Nm1·Nm2. 例4.2设f(x)=(x3+3)(x2+1)(x2+2)(x2-2).证明:对每个正整数m,f(x)≡0 (modm)恒有解. 例4.2的证明由例4.1可知,我们只需对“m=pn,其中p是素数”进行证明. 对n进行归纳. (1) 当p=2时,显然x0≡1 (mod22)是x3+3≡0 (mod22)的一个根. 我们假设x1是x3+3≡0 (mod2n)的根,即2a刚好整除x13+3,其中a≥n.记x13+3=2ay1,其中y1是奇数. 由于 (x1+2a)3+3≡x13+3x12·2a+3(mod2a+1) ≡2a(y1+3x12)(mod2a+1) ≡0(mod2a+1), 则x2=x1+2a是x3+3≡0 (mod2n+1)的根. 归纳假设x1是x2-t≡0 (modpn)的根. 记x12-t=pnz,其中z是整数. 注意到(x1,p)=1, 则存在整数s,使2x1s≡1 (modp). 记x2=x1-zspn, 则 x22-t=(x1-zspn)2-t ≡(x12-t)-2x1szpn(modpn+1) ≡pnz-zpn(modpn+1) ≡0(modpn+1). 即x2是x2-t≡0 (modpn+1)的解. 因此, (x2+1)(x2+2)(x2-2)≡0 (modpn)恒有解. 例5.1证明任意n阶矩阵A的伴随矩阵A*可表示为A的多项式. 若A的秩等于n-1,则0是A的特征值,此时存在可逆矩阵P,使得 根据中国剩余定理可得,存在多项式f(λ),使得 于是 =f(P-1AP). 进而 P*A*(P-1)*=P*A*(P*)-1=P-1f(A)P, A*=(P*)-1P-1f(A)PP*=(PP*)-1f(A)(PP*)=f(A). 综上可得,n阶矩阵A的伴随矩阵可表示为A的多项式. 设A是n阶矩阵,m是正整数.若矩阵X满足Xm=A,则称X是A的m次根.一般情况下,A的m次根不一定存在,即使A的m次根存在,它也不一定能表示为A的多项式.具体参见文献[5]. 例5.2设n阶复矩阵A满足rank(A2)=rank(A),m是正整数.则存在矩阵X满足Xm=A,且X可表示为A的多项式.即此时A存在一个m次根X一定可表示为A的多项式. 其中 这里,ri1≤ri2≤…≤riti=mi.记Jri=λi(Iri+Nri),其中 根据Taylor公式可得 (8) 其中k是任意正整数且gk(x)是关于x的形式幂级数. 容易计算得 其中 因此,X=g(A). 当A可逆时,上面的证明思路仍然是适用的. 例6.1设a、b都是整数.若对任意正整数n,均有an+n整除bn+n,则a=b. 例6.1的证明假设a≠b,从条件可以验证b-a=±1是不可能的.取素数p不整除b-a.根据中国剩余定理,存在正整数n,满足 若p|a,则p|n,p|an+n.又an+n|bn+n, 则p|bn+n,p|b,进而p|b-a.矛盾.因此,p不整除a. 由Fermat小定理可得ap-1≡1 (modp),于是 an+n≡a+n≡0 (modp), 进而p|bn+n,注意到p不整除n,p不整除b.再根据Fermat小定理可得bp-1≡1 (modp),由此可得 bn+n≡b+n≡b-a(modp). 这与p不整除b-a矛盾. 例6.2证明下面关于x1,x2,x3,x4,u,v,w的方程组 有无穷多组正整数解. 例6.2的证明记a=12+22+32+42,b=13+23+33+43,c=15+25+35+45.设x1=axbycz,x2=2axbycz,x3=3axbycz,x4=4axbycz.则方程组变为 (9) 要证方程组(9)有无穷多组正整数解,只需证明下列3个关于x、y、z的同余方程组都有无穷多正整数解即可. 解得x=12+30α,y=15+30β,z=10+30γ,其中α、β、γ为自然数. 即原方程组有无穷多组正整数解. 我们现在考虑如下非常重要的赋值映射. 显然vp是满射. 例6.3设m是正整数,a是整数.证明存在正整数n,使 v2(n!)≡a(modm). 例6.3的证明设m=2αl,其中α是自然数,l是奇数.由Euler定理可得2φ(l)≡1 (modl),其中φ(l)是Euler函数. 根据中国剩余定理,存在正整数u,满足 对1≤i≤u,取正整数ki,记αi=kiφ(l)+1,使得 α<α1<α2<…<αu, 此时 2αi-1=2kiφ(l)+1-1=2·(2φ(l))ki-1≡1 (modl), 现记n=2α1+2α2+…+2αu,可以验证 v2(n!)=n-u =(2α1-1)+(2α2-1)+…+(2αn-1) ≡u≡a(modl), v2(n!)=n-u≡-u≡a(mod2α). 因此,v2(n!)≡a(modm). 例6.4设p1,p2,…,pn是两两互异的素数,a1,a2,…,an均是整数.若ε>0,则存在整数x,使得|x-ai|pi<ε,其中1≤i≤n. 证取充分大的整数e1,e2,…,en使pi-ei<ε,其中i=1,2,…,n.根据中国剩余定理,存在整数x,满足 此时piei|x-ai,从而|x-ai|pi≤pi-ei<ε.


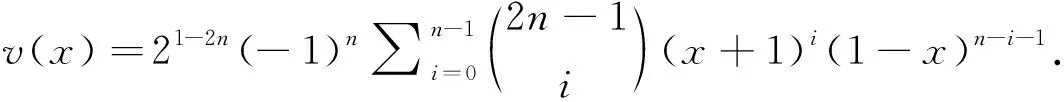
2 从整线性方程组AX=b的角度出发
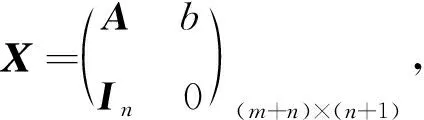
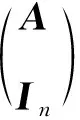

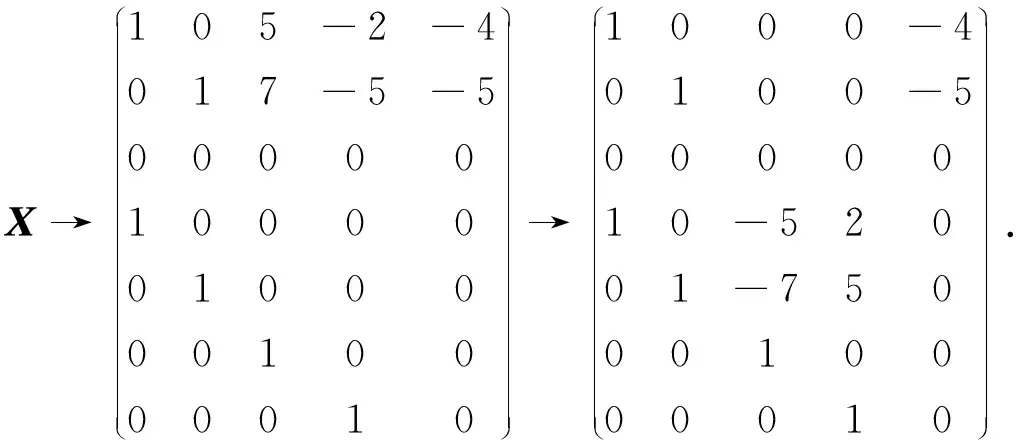
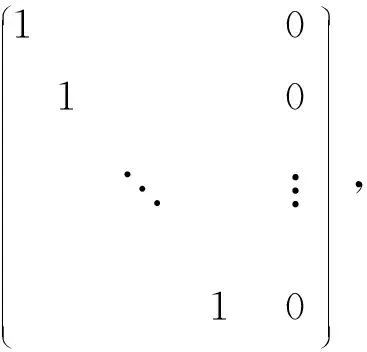


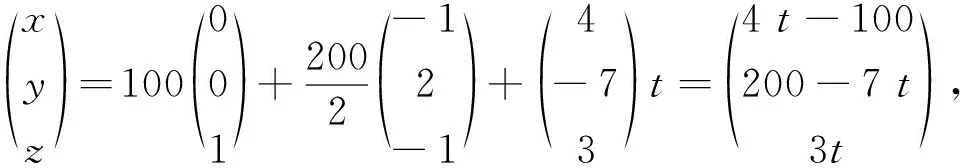
3 在数论里的若干应用
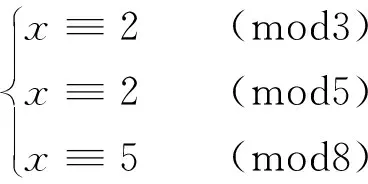
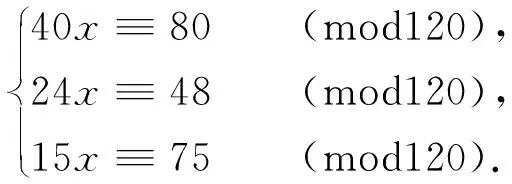
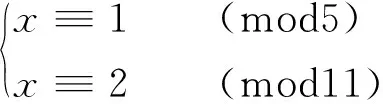
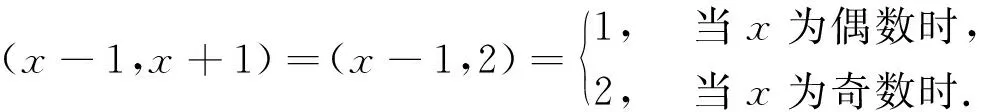
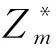
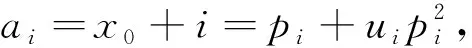
4 在多项式里的应用
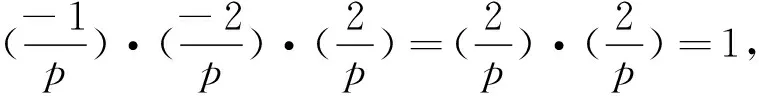
5 在矩阵论中的应用
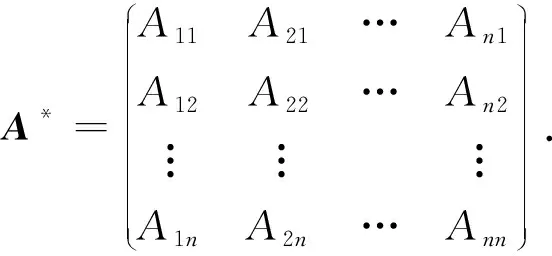
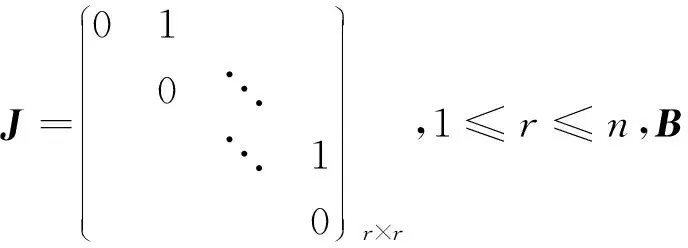
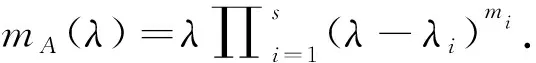
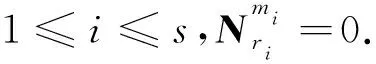
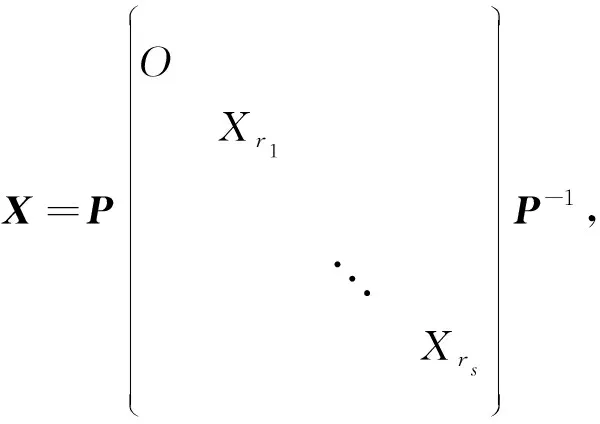
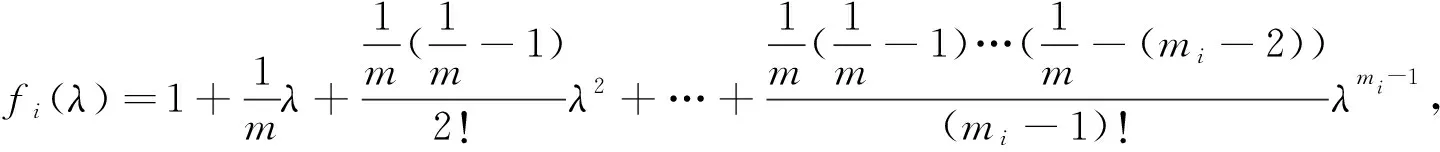
6 杂题