基于ANSYS_Workbench的深海取样外筒多目标优化设计

付 平，殷 硕，张明赛，王晨旭

(青岛科技大学 机电工程学院，山东 青岛 266061)

近几年，深海浮游微生物的研究吸引了大批科学家们的关注[1]，深海浮游微生物一般生活在深海、高压的黑暗环境中，是一种新兴的生物资源，具有较高的科研价值。浮游微生物能够在恶劣的环境下生存，具备了浅海和地面生物所不具备的基因，因此研究深海浮游微生物的在生命的起源、生物学、新型基因和药品的研发以及环境保护等许多方面都有着重要的意义[2]。取样筒在研究深海浮游生物过程扮演重要角色。在深海取样筒下端管道外接蓄能器，预先将取样筒的压强调为取样地点的实际压强，当取样过程完成后，取样管道阀门关闭，保压管道阀门打开，使取样筒实现保压功能[3-4]。取样外筒在整个取样过程中至关重要，是收集深海浮游微生物的重要容器。

优化通常指的是设计结果的最大化或者最小化，优化设计可以很大程度上提高零件的综合性能[5]。优化设计中使用频率较高的模块是Design Exploration多目标驱动优化分析模块。为了让物体的多个输出结果实现最优，往往需要提供多个优化目标。目前，互联网的飞速发展使基于CAE技术的优化设计得到了较大发展，并且应用于众多实际工程设计当中。

1 三维模型的建立

深海浮游微生物的取样主要依靠取样系统，其三维结构如图1所示。

图1 取样系统结构Figure 1 Structure of sampling system

取样筒是取样系统中的重要组成部分，其设计放弃了传统法兰结构，采用“双层筒体+活塞”结构[6]。如图2所示，取样筒双层桶体间填充保温材料，防止温度出现变化；同时在保温材料层与内胆间放置小型温度传感器，以实时监测温度情况。活塞为一倒置圆筒形结构，活塞底部采用固定圈将微生物滤膜固定于活塞上，使滤膜与活塞间形成一封闭腔。取样时大量海水由上方入口涌入，经微生物滤膜过滤，其余海水则由筒壁下方出口排出，深海浮游微生物被截留在活塞腔内，得到高浓度浮游微生物海水样本。内胆与活塞间则采取支撑环固定，活塞上有2个孔，分别连接一个进入方向与导出方向的单向阀，桶体上开有一个洞，连接一个三通管，三通管的另外两端一端连接蓄能器，另一端连接电磁阀作为控制出口。优化既要满足储存样本的空间需求，又要实现取样筒的质量轻量化，并且能够让取样外筒的综合强度得到较大提高。

图2 主体取样筒结构Figure 2 Structure of main sampling cylinder

此次优化只对取样外筒进行参数优化，在SolidWorks软件中进行取样外筒的设计，其结构如图3所示。

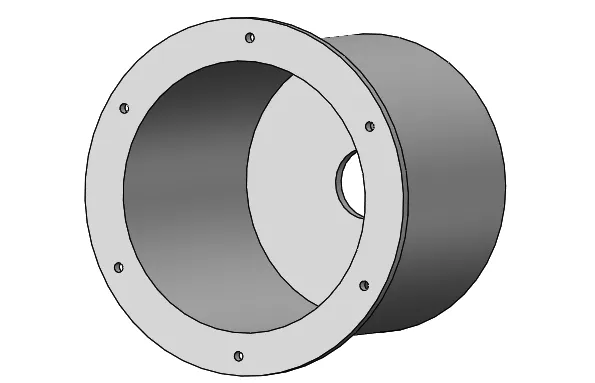
图3 取样外筒结构Figure 3 Structure of outer sampling cylinder

2 取样外筒的有限元分析

2.1 模型导入和材料添加

课题组采用SolidWorks对取样筒进行三维建模，并将三维模型导入Workbench中进行参数优化。优化之前，首先设置参数的变量名。将“DS_”加在每个参数的变量名前,方便参数的识别。打开Workebnch软件，依次点击Static Structure，Geometry，在Geometry中点击Import，导入取样外筒三维模型。在Geometry中查看导入的模型，可以看到所有的设计参数均被识别，点击设计变量前端的方框，出现“P”字样的，设置为后续优化的参数。

材料选择7075铝合金，密度为2 850 kg/m3，弹性模量为71 GPa，泊松比为0.3，屈服强度是455 MPa，抗拉强度是524 MPa。

2.2 划分网格

在静力学分析模块Model中点击Generate Mesh进行系统自动网格划分，观察网格的质量。为了进一步提高网格质量，兼顾计算精度和速度，重新选择网格划分的方法，点击Mesh-insert-Method，在Geometry中选择整个三维模型，选择Patch Independent，将最小尺寸限制定义为1 mm。网格划分如图4所示，网格质量分布柱状图如图5所示。从图5可以看出，取样外筒的元素数量基本集中在0.9左右，说明网格质量良好。

图4 网格划分Figure 4 Meshing

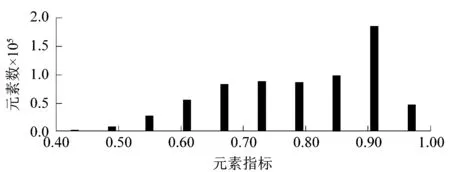
图5 网格质量Figure 5 Mesh quality

2.3 施加约束和载荷

取样筒在工作时，整个取样系统固定在支撑架上，所以在取样外筒的顶端施加固定约束Fixed Support。在深海的取样过程中，搭载蛟龙号的深海取样装置一般能够下潜到深海6～7 km，取样外筒的裸漏部位会受到海水的挤压，对取样外筒的外壁沿径向施加压力，施加的径向力为30 MPa；对取样外筒的筒底沿Y轴方向施加轴向力为28 MPa。

2.4 求解

在Solution上选择整体变形量、等效应力和等效应变，并求解。最终获得取样外筒的整体变形云图、等效应力云图和等效应变云图如图6～8所示。

图6中取样外筒的外壁变形量由两端向中间呈阶梯状递增，其中筒壁中间的变形量最大，为14.459 μm，远小于取样外筒的限定最大变形量48.000 μm。因此，结构设计符合要求，可以进行进一步地优化。

图6 整体变形量云图Figure 6 Overall deformation nephogram

图7所示的等效应力云图可以看出，等效应力最大值为188.79 MPa，小于7075铝合金的屈服极限值455.00 MPa，并且有相对较大的应力值的安全范围。由图7可知，取样外筒外壁四周所受应力较小，中间部位所受应力相对较大，外壁正面所受应力呈对称分布，均在合理范围内。取样外筒底部承受应力较大，底部出口处承受应力值最大。

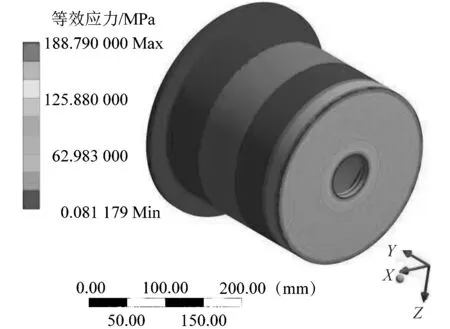
图7 等效应力云图Figure 7 Equivalent stress nephogram

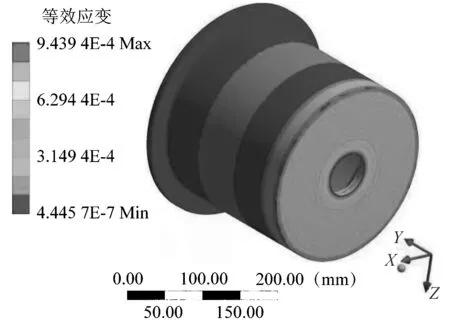
图8 等效应变云图Figure 8 Equivalent strain nephogram

3 灵敏度分析

3.1 实验对象的选取

在取样外筒的轻量化过程中，如果只考虑取样外筒的质量，可能会由于质量的改变导致取样筒的其他性能发生变化，需要考虑的因素包含取样外筒的最大等效应力和最大变形量[7]。所以在参数灵敏度分析当中，除了要分析各个输入参数对最大等效应力和最大变形量的影响之外，还要分析各个输入参数对质量的影响。

实验因子包含取样外筒的质量、取样外筒最大等效应力和取样外筒最大变形量。

3.2 设计参数

灵敏度分析不仅可以显示设计变量对输出结果的影响，而且能够直观的看出各设计变量对于输出结果影响程度的大小，因为设计变量都不是单一的，所以需要灵敏度分析[8]。通过分析，可以得出灵敏度柱状图，显示出3个设计参数对目标结果影响程度的大小。灵敏度分析柱状图如图9所示。

图9 灵敏度柱状图Figure 9 Sensitivity histogram

由图9可知，取样外筒的半径D1和取样外筒外壁的厚度D5这2个设计参数对输出结果的影响较大，这2个设计参数对每个输出结果的灵敏程度都在0.6以上；取样外筒的高度D6的灵敏度在0.5左右。

4 响应面的构建

4.1 参数设置

实验设计方法是设计空间内测试样本的有效方法，是从所有实验因子组合中选出最合适的组合进行测试的方法，通过模拟数据的方式替代实际测试，达到降低设计成本和缩短实验周期的效果[9]。将3个设计参数D1，D5，D6设定为输入参数，将取样外筒的的质量、取样外筒所受最大等效应力以及取样外筒最大变形量设定为输出结果，设定设计参数的变化范围如表1所示。

表1 设计参数的变化范围Table 1 Variation range of design parameters

课题组采用了最优填充空间设计法，设计空间内均分分布所有设计点，空间填充能力强，能够覆盖整个空间，对后期构建响应面模型做好铺垫。样本点类型为自定义，设计类型为最大熵，设计样本点数为30，最大编码数为10，系统基于Monte Carlo抽样技术自动生成各设计参数点，最终可以得到全部设计参数的计算结果，用作后期响应面的拟合数据[10]。

4.2 模型的建立

响应面法是一种搭建近似模型的方法，利用筛选实验来选定优化方向，按照质量最轻方向和满足约束条件寻找最优解，规定好收敛条件，就能够得到最佳设计结果。其模型构建的优点是精度高，并且可以同时显示预测位置的预测误差和预测值[11-12]。采用最小二乘法，进而拟合出一个响应面函数，从而得到近似的模型，并将原来的隐形函数关系变成显式函数，建立起输出结果与设计参数之间的明确关系。通常情况下，响应面模型选用比较精准的二阶模型，n个设计变量的二次多项式模型可以表示为：

式中：G(x)为拟合函数；x为设计变量；ε为随机误差；x=(x1,x2,…,xn)；α0,αi,αii,αij为待定系数，其个数共有Z=(n+1)(n+2)/2，未知参数由最小二乘法确定时，实验点数必须大于Z。

二次多项式构建完之后，进行数学模型的建立。优化设计的3要素分别为设计变量、目标函数和约束，得到取样外筒设计参数与输出结果之间的近似函数关系之后[13]，建立取样外筒优化设计的数学模型，如下所示：

minS(X)=min [S1(X),S2(X),S3(X)]。s.tS2(X)≤455 MPa;S3(X)≤0.048 mm;112.5 mm≤x1≤137.5 mm;12.6 mm≤x2≤15.4 mm;11.7 mm≤x3≤14.3 mm。

式中：S(X)为目标函数;S1(X)为质量;S2(X)为最大应力;S3(X)为最大变形。x1为取样外筒的半径;x2为取样外筒外壁的厚度;x3为取样外筒底端厚度。

根据Kriging模型，利用协方差函数对平均值为0的随机过程进行插值，从而得出模拟设计参数与目标结果之间的响应关系[14]。设计点观测值与响应面函数预测值之间的数值分布如图10所示。从图中可以看出，所有的点均匀分布在与横坐标呈45°的同一条直线上，说明其拟合精度很高。

图10 归一化图Figure 10 Numerical value distribution diagram

从图11可以看出，变量D1和D5与取样外筒的质量呈正相关关系，质量随着设计变量D1和D5的增大而增大，在D1和D5最大点处，质量最大。

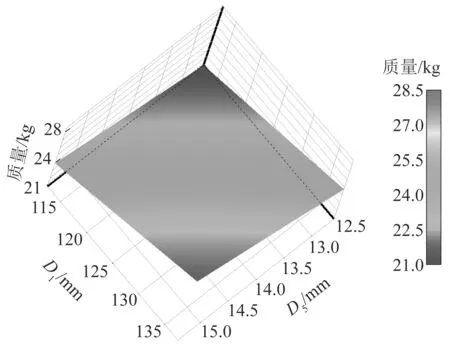
图11 质量响应面Figure 11 Mass response surface

从图12可以看出，最大变形随着D1的增大而增大，呈正相关。而最大变形随着D5的增大而减小，呈负相关。当D1取得最大值时，最大变形量最大，当D5取得极小值时，最大变形量最大。

图12 最大变形响应面Figure 12 Maximum deformation response surface

从图13可以看出，D5对取样外筒最大等效应力影响较小，D1对取样外筒最大等效应力影响较大，最大等效应力随着D1的增大而增大，呈正相关。最大等效应力随着D5的增大而减小，呈负相关。

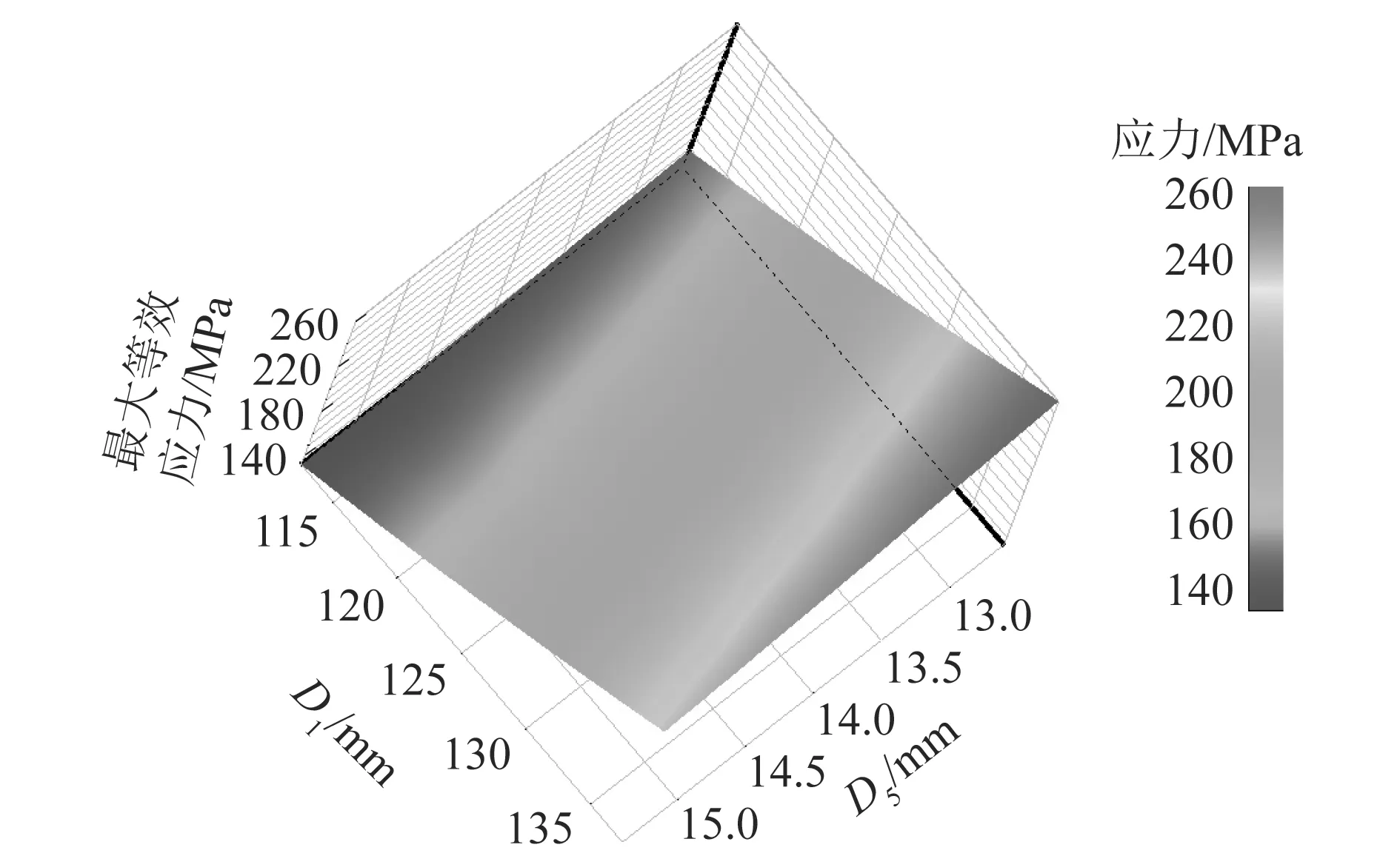
图13 最大等效应力响应面Figure 13 Maximum equivalent stress response surface

4.3 多目标遗传算法求最优解

多目标遗传算法是在自然环境条件下，通过仿真生物的遗传和进化，不断淘汰和进化过程，逐渐形成的一种遗传算法。在满足所有约束和各个目标函数的条件下，求解一组最优解集。多目标遗传算法[15-17]为处理多个设计目标之间存在矛盾的状况提供了设计思路，效率较高。

通过ANSYS_Workbench中的Optimization模块进行优化计算得到以下3组备选设计点如表2所示。

表2 备选设计点Table 2 Alternative design points

4.4 分析优化结果

由表3可知，3组设计点的最大变形都没超过48 μm，最大等效应力都没超过材料的许用应力455 MPa，因此3组设计点均符合要求。优化的主要目的是在满足取样外筒质量最轻化的前提条件下，尽可能让取样外筒的最大变形和最大应力降低，使其综合强度得到提高。综合分析，排除设计点Ⅰ，Ⅲ，选择设计变量Ⅱ为最优设计点。与优化前的参数相比较，质量降低了11.27%，最大变形降低了14.89%，最大等效应力降低了26.70%，Ⅱ组质量降低的最大，满足质量最轻化需求，是本次优化的最优结果。多目标优化前后比较结果如表3所示。

表3 多目标优化前后结果比较Table 3 Comparison results before and after multi-objective optimization

5 结语

课题组采用ANSYS_Workbench软件对深海浮游微生物取样外筒进行优化设计。首先，对取样外筒进行有限元分析，得到取样外筒整体变形云图、等效应力和应变云图；然后，运用响应面法进行优化，拟合出设计变量与输出结果之间的函数关系，并构建数学模型，采用多目标遗传算法，生成优化设计的Pareto解集，考虑和分析所有输出结果；最后，分析和比较所有数据，确定最优设计点并得出最优参数尺寸。与优化前的参数相比较，质量降低了11.27%，最大变形降低了14.89%，最大等效应力降低了26.70%。优化后既实现了取样外筒的质量轻量化，又能显著提高取样外筒的综合性能，优化结果较好，并且可以进一步调整整体结构的尺寸，让主体取样筒达到最优化。