折叠式柔性关节设计及运动学建模

杜静恩，许 勇，贾云博，刘佳莉，赖磊捷，徐 蕊

(上海工程技术大学 机械与汽车工程学院，上海 201620)

折纸是一门起源于中国的古老民间手工艺术,6世纪时传入日本[1]。20世纪初,Yoshizawa提出了折纸符号系统,大大促进了折纸艺术的发展[2]。折纸和剪纸可以将平面材料变成可拉伸、可折展和具有多重稳定性的三维关节机构[3]。这些由于材料的折叠产生的特性被用于航天器材[4]、建筑制造[5]、电子能源[6]、化学传感[7]和生物医学[8]等领域。

近年来，越来越多学者尝试着将折纸原理应用到了机器人构型的开发设计中，保留折纸的空间可折展等特性并结合工业机器人自动作业的优势，使得折纸机器人对作业环境有更好的适应性。折纸机器人是指通过对自身形态的折叠变形来实现对应功能的自动化机器[9]，即通过对材料的折痕设计使其在折叠后具有特定的三维形态，进而实现相应的功能[10]。这类机器人往往对材料性能有一定的要求，用于制造折纸机器人的纸张或其他可折叠薄片材料在显著减少机器人重量和降低材料成本的同时也有利于环境保护[11]。

我们可以通过折纸技术来实现对机构的柔性设计，将现代平面制造技术如光蚀刻、激光切割和3D打印等与折叠式设计方法相结合的方案无疑是一种非常高效且实际的选择。折叠技术可以根据需要定制折叠方式完成特定的任务，高效快捷，其重构性又大大降低了成本。

课题组基于折纸机构的柔顺性和可折展性，设计出可以实现局部扭转和摆转的折叠式柔性复合关节，建立了折叠式柔性复合关节的运动学模型，并对折叠式柔性复合关节的驱动空间、关节空间和操作空间之间的映射关系进行了分析。

1 折叠式柔性复合关节

1.1 折叠式柔性复合关节组成

课题组提出的折叠式柔性复合关节包含的基本关节为折叠式扭转关节和折叠式摆转关节，二者组合而成的折叠式柔性复合关节如图1所示。

图1 折叠式柔性复合关节Figure 1 Folding flexible composite joint

1.1.1 折叠式柔性扭转关节

图2(a)所示为折叠式扭转关节展开后的折痕，其中粗实线为关节的边界或山折痕，粗虚线为谷折痕，折叠后就成了图2(b)所示的带有扭转功能的三维模型。

图2(b)中O1和O2分别为动、定平台形心，动定平台发生绕O1O2轴的相对扭转。

1)支撑平台及挡板

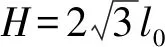
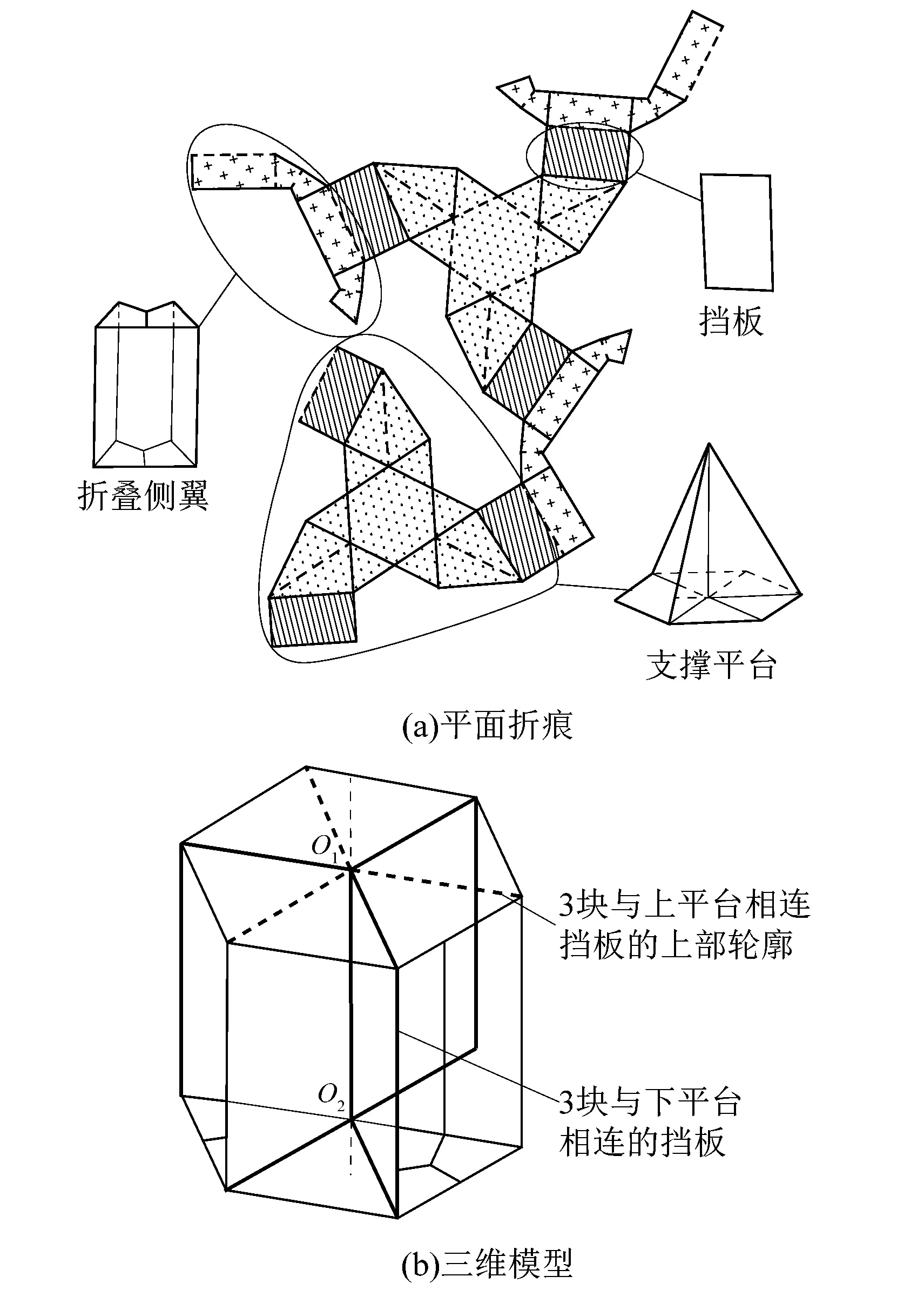
图2 折叠式扭转关节展开与折叠效果图Figure 2 Renderings of expansion and folding of folding torsion joint

图3 单个支撑平台与挡板折叠展示Figure 3 Single support platform and baffle folding display

按峰谷折痕分别折叠，折叠时点G1,G2,G3,G4,G5,G6重合于正六边形ABCDEF的形心O1处，点H1,H2,H3在最后重合于点Hi处。

支撑平台分上下2个，上下平台的折痕与折叠方法基本一致，2平台连接的3个挡板分别连接3个折叠侧翼的两侧使之成为一个整体。

2)折叠侧翼

折叠侧翼为图4中的阴影部分，将其单独拆开做展示。折叠侧翼的竖直侧板A1B1C1D1和A2B2C2D2为矩形；称A2B2F2E2,A1B1F2E2,C1D1E1F1和C2D2E1F1为折叠板。

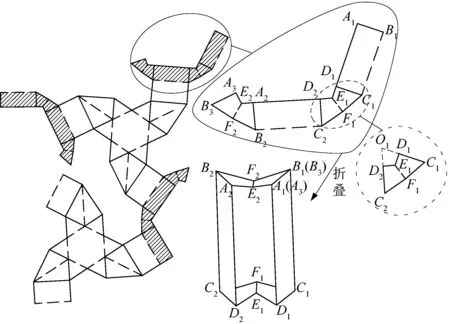
图4 折叠侧翼折痕及三维效果Figure 4 Folded flank creases and 3D effect

对图形D1C1F1C2D2E1∶C1D1的延长线与C2D2的延长线交于点O1，△C1O1C2为边长为2l0的等边三角形；E1D1,E1D2,E1F1分别垂直平分O1C1,O1C2,C1C2。折叠时将A1,A3重合，B1,B2重合形成结构闭环。

为计算驱动绳长度，引入参数：面A2B2F2E2与面A2B2C2D2的夹角∠E2A2D2=θ1；面A2B2F2E2与面A1B1F2E2的夹角∠B2F2B1=θ2；面A2B2C2D2与面A1B1C1D1始终在竖直平面内，设两个面的二面角为扭转角φ，则有：∠A1O2A2=φ。

折叠侧翼折叠过程中，按峰谷折痕折叠，从图5中俯视图和三维图可以看到随着φ值的变化折叠侧翼的变化情况。

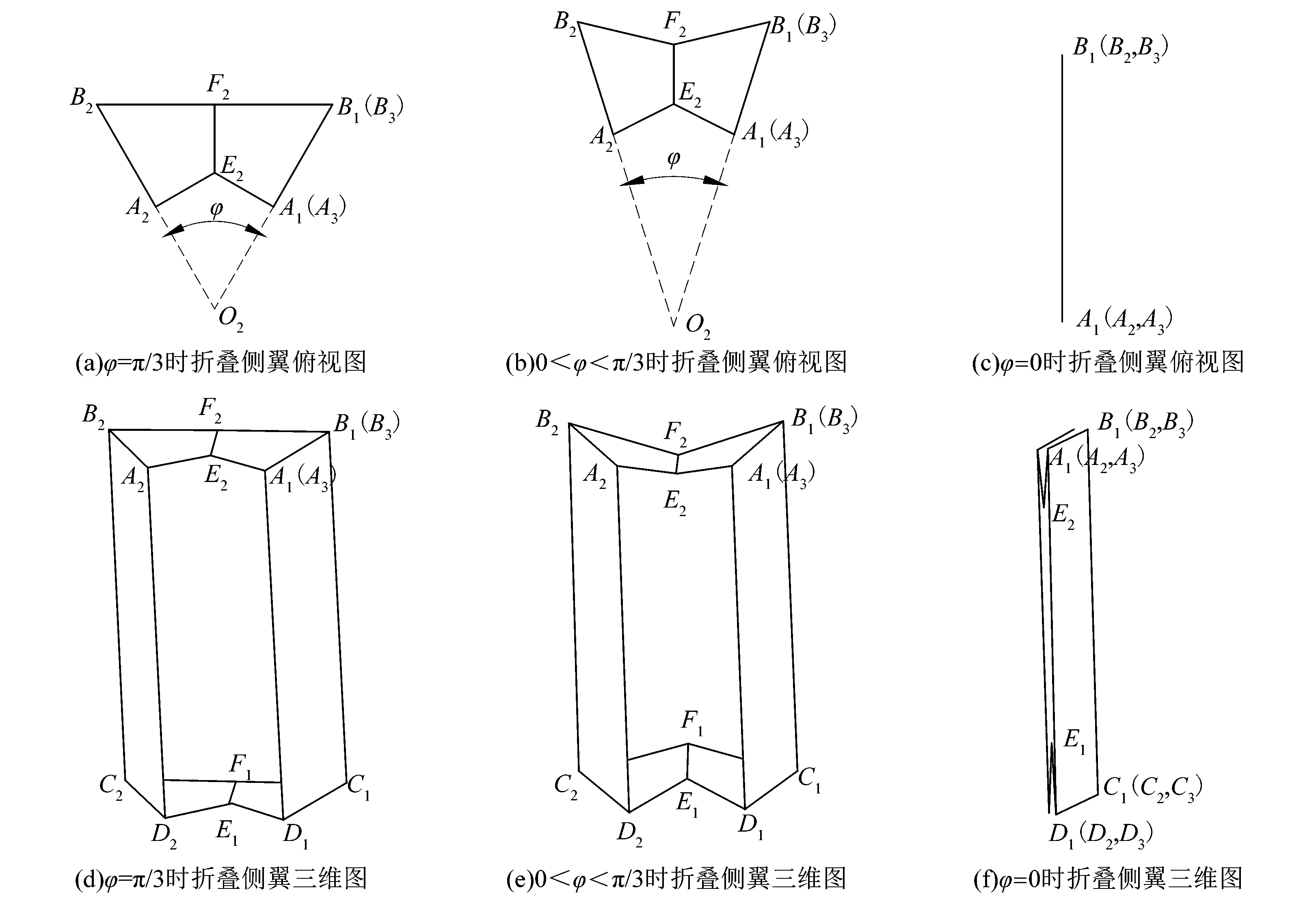
图5 折叠侧翼变形展示Figure 5 Folded flank deformation display

扭转关节在驱动绳放松状态时，由于折叠侧翼2个竖直板绑有弹力绳，折叠侧翼合拢；驱动绳受外部拉力后，折叠侧翼的2个竖直板被撑开，从而使上下支撑平台发生相对扭转。

图6所示为折叠扭转关节的4个状态。状态Ⅰ，φ=0时，折叠侧翼完全折叠；状态Ⅱ，0<φ≤π/6和状态Ⅲ，π/6<φ<π/3，这2种状态的区别在于驱动空间到关节空间的驱动绳长计算方式不同，但对于关节空间到操作空间计算完全相同；状态Ⅳ，φ=π/3为折叠式扭转关节的最大扭转角，折叠侧翼呈完全展开状态。

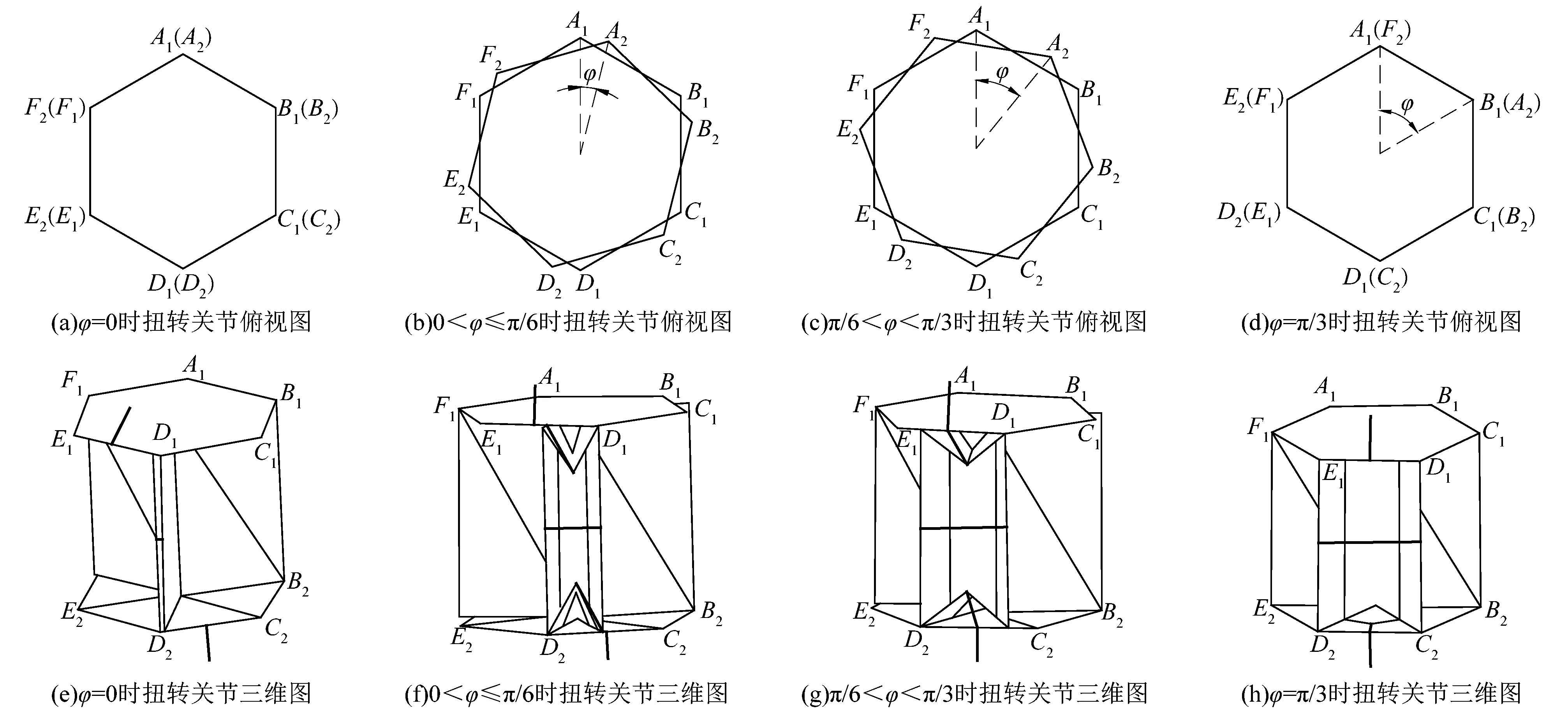
图6 折叠式扭转关节运动状态Figure 6 Rotation process of folding torsion joint

1.1.2 折叠式柔性摆转关节设计

图7(a)所示为折叠式摆转关节完全展开后的折痕，图7(b)所示为折叠后具有摆转功能的三维模型。

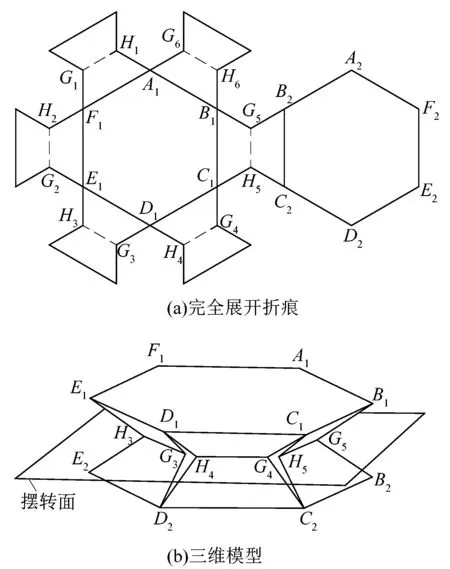
图7 折叠式摆转关节Figure 7 Folding swing joint

图7(b)中的摆转面指折叠式摆转关节变形时摆转面两侧关于摆转面是镜像的，且HiGi痕在摆转面上。其中，i=1,2,…,6。

上下底面A1B1C1D1E1F1与A2B2C2D2E2F2都是边长为2l0的正六边形。A1B1C1D1E1F1各边与各个HiGi折痕都构成等腰梯形，且折痕HiGi的长度都为l0。为方便描述，下文将图形A1B1H6B2A2G6,B1C1H5C2B2G5,C1D1H4D2C2G4,D1E1H3E2D2G3,E1F1H2F2E2G2,F1A1H1A1F1G1称为折叠支撑板。

在不受力的情况下六边形A1B1C1D1E1F1与A2B2C2D2E2F2处于平行状态，折叠式摆转关节可以根据工作需求调整摆转角度φ与上下位移量h，如图8所示。

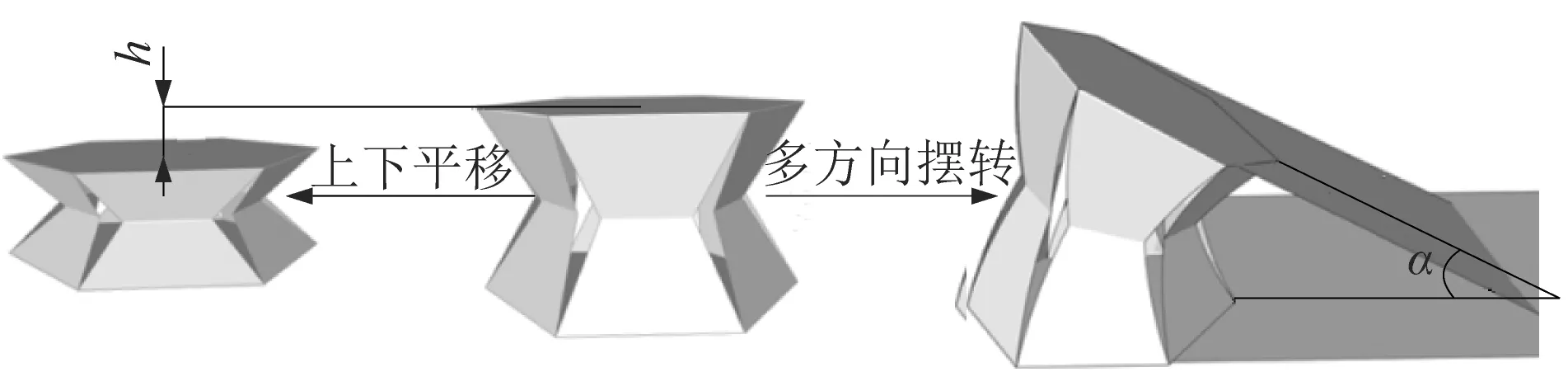
图8 折叠式摆转关节2种变形方式Figure 8 Two deformation modes of folding swing joint

1.2 折叠式柔性复合关节设计

在设计折叠式扭转关节和摆转关节时2种关节的动定平台都为边长为2l0的正六边形。先将多个折叠式摆转关节串联(课题组选取3个折叠式摆转关节串联)，再将折叠式扭转关节的动平台串联在折叠式摆转关节串联体的定平台上，串联为折叠式柔性复合关节。

2 折叠式柔性复合关节运动学建模

2.1 折叠式柔性关节运动学建模

2.1.1 折叠式扭转关节

设下支撑平台为定平台，以正六边形形心O0为定平台坐标系原点，以定平台所在平面的向上法线方向为Z0轴正方向，以O0A0方向为X0轴正方向，最后由右手定则确定Y0轴正方向，建立DH坐标系O0-X0Y0Z0；以上支撑平台正六边形形心O1为原点，以垂直于平面向上方向为Z1轴正方向，以O1A1方向为X1轴正方向，最后由右手定则确定Y1轴正方向，建立DH坐标系O1-X1Y1Z1如图9所示。

图9 折叠式扭转关节坐标系和几何模型Figure 9 Coordinate system and geometrical model of folding torsion joint

图9中的O0O1为动定平台发生相对扭转时的转轴，在最初时动平台与定平台坐标系夹角为0,在发生相对扭转后动平台与定平台坐标系夹角为φ。

在运动过程中上下支撑平台始终只发生相对扭转，任意时刻扭转角为φ时坐标系O1-X1Y1Z1相对于O0-X0Y0Z0的变换矩阵为：

(1)

相反，扭转关节的操作空间到关节空间的关系是已知末端关节位姿，对扭转关节的扭转角φ进行求解。设坐标系O0-X0Y0Z0各轴上的单位矢量为n,o,a；动坐标系O1-X1Y1Z1原点O1到定坐标系O0-X0Y0Z0原点O0的位置矢量用p表示。

现矢量n,o,a,p相对坐标系O0-X0Y0Z0的矩阵为

(2)

将式(1)和式(2)联立得

φ=arccosoy。

(3)

式(3)即为扭转关节关节空间到操作空间的运动学逆解。

驱动绳的一端系在折叠侧翼(以下端为例)相邻折叠板外侧重合点Q处,穿过折叠板活动区对应的平台边的中点P，我们将绳在QP间的长度称为驱动绳长l。随着驱动绳长度l的变化，扭转关节的扭转角度φ也会发生向相应的变化。绳子在关节的整个扭转的过程中有2种不同的状态，具体如图10所示。

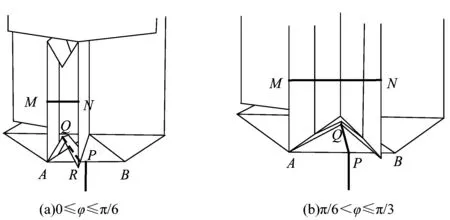
图10 折叠式扭转关节驱动绳状态变化Figure 10 States change of drive line of folding torsion joint

当0≤φ≤π/6时，由于折叠侧翼的竖直侧板在AP段，l为QR,RP长度之和,如图10(a)所示；当π/6<φ≤π/3时，由于折叠侧翼的竖直侧板在PB段，l等于PQ长度,如图10(b)所示。

图10中的点M,N为竖直侧板外侧边线中点，2点间拴细弹力绳用于使折叠侧翼恢复初始状态。R为折叠侧翼的竖直侧板在AP段时驱动绳与竖直侧板的接触点；Q为折叠板外侧重合点。

设初始状态时绳子的原长

在第1种状态下驱动绳长为线段QR+RP，此时扭转角φ∈[0,π/6]，这一段的绳长的数学模型为：

(4)

其中：

这里的γ和l0是计算过程中为了方便计算和结果显示给出的中间变量，对最终结果没有影响。

在第2种状态下，此时扭转角φ∈(π/6,π/3]，绳长的数学模型为：

(5)

可以求得驱动绳长l与扭转角φ间的关系为：

(6)

式(6)即为关节空间到驱动空间的运动学分析。

由于式(6)的2个等式都只有1个自变量φ与1个因变量l，用式(6)求得的逆解就是驱动空间到关节空间的运动学分析。

2.1.2 折叠式摆转关节

折叠式摆转关节没有刚性扭转和移动，使用绳线驱动来使动平台发生位姿变换。折叠式摆转关节的关节空间参数包括：单个摆转关节的动平台发生摆转时与定平台形成的二面角为摆转角α；单个摆转关节动平台发生摆转时(即摆转角α存在时)垂直于动定2个平台交线的面与定平台X轴的夹角为方位角β；单个摆转关节动平台仅发生上下平移但不发生摆转时(即摆转角α不存在的时候)，动平台在进行沿Z轴的移动时与动平台初始位置的距离为伸缩位移h。

以正六边形的形心Oi(定平台i=1，动平台i=2)为坐标系的原点，以QiAi方向为Xi轴正方向；以正六边形所在面法线的向上方向为Zi轴正方向，用右手定则确定Yi轴正方向建立如图11所示坐标系。

A1,C1，E1为驱动绳穿过定平台孔径的中心，在第i个摆转关节定平台建立坐标系Oi-XiYiZi(i=1,2,3,…,n)；动平台建立动坐标系Oi+1-Xi+1Yi+1Zi+1。直接相连的串联体的接触面的动定坐标系重合，故可以认为第i个关节的动坐标系与第i+1个关节的定坐标系是同一个坐标系。当摆转关节在竖直状态时摆转角αi，方位角βi和伸缩位移hi均为0。

以摆转关节在竖直位置时为初始位置，3条绳的长度LAi,LCi,LEi均等于中央支撑弹簧长度L，即LAi=LCi=LEi=L。当摆转关节上下收缩时(即动平台相对于定平台仅在竖直方向进行平移),每根驱动绳长度变化量为ΔLAi=ΔLCi=ΔLEi=hi，如图12(a)所示。

图12 单个折叠式摆转关节几何模型Figure 12 Geometrical model of single folding swing joint

当摆转关节因绳驱发生弯曲时，将整个运动过程分解为：从定坐标系Oi到动坐标系Oi+1之间的平移和以定坐标系Yi,Zi轴为旋转轴的旋转。当关节受绳驱动发生摆转后摆转角为αi，方位角为βi时，此时动平台坐标系相对于定平台坐标系位置和姿态都发生了相应的变化，3个方向上的绳长也发生变化，摆转关节靠3个方向上的驱动绳长度变化实现摆转和上下收缩。

定平台的坐标系与动平台的坐标系间的关系用DH法推导并得到变换矩阵T，完成摆转关节从关节空间至操作空间的运动学分析。这种整体的变换可以分解为多个变换实现：从定坐标系中心点Oi平移至动坐标系中心Oi+1，绕Zi轴扭转βi，绕Yi轴扭转αi，绕Zi轴扭转-βi得到齐次变换矩阵。联立平移矩阵和扭转矩阵，得到Oi坐标系到Oi+1坐标系的齐次变换矩阵T为

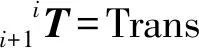
计算得：

(7)

式中：L表示摆转关节在初始位置的时候驱动绳的长度；αi取值范围为[0,π/3]；βi取值范围为[0,2π]。

由于串联摆转关节是由多个摆转关节串联而成的，故由n个摆转关节串联而成的串联摆转关节中，从第1个摆转关节的定坐标系到第n个关节的动坐标系的齐次变换矩阵为：

(8)

式(8)表示了串联摆转关节的关节空间与操作空间的映射关系，即关节空间到操作空间的运动学关系。

相反串联摆转关节的操作空间到关节空间的关系是已知末端关节位姿，对串联摆转关节各个关节的摆转角α和方位角β进行求解。设坐标系Oi-XiYiZi各轴上的单位矢量为n,o,a；动坐标系Oi+1到定坐标系原点Oi的位置矢量用p表示。

以3个摆转关节串联为例，现已知第3个摆转关节动平台O4相对于第1个摆转关节定平台O1的位姿，则矢量n,o,a,p对应坐标系O1-X1Y1Z1的矩阵为

(9)

联立式(8)和式(9)可以求得：

(10)

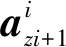
式(10)即为操作空间到关节空间的运动学分析关系式。

在摆转关节运动过程中，当摆转角αi和方位角βi确定后，则动定平台间的3根绳长度LAi,LCi和LEi可以分别确定。当摆转关节弯曲到任意位姿时，过动定平台与绳的交点Ai,Ci和Ei作OiP线的垂线，垂足分别为Ai0,Ci0和Ei0,L0为动定平台间弹簧的中心轴线，如图13所示。

图13 单个折叠式摆转关节弯曲任意角度模型Figure 13 Flexed mode at any angle of single folding swing joint

可得出AiAi0∥Ai+1Ai+10,CiCi0∥Ci+1Ci+10,EiEi0∥Ei+1Ei+10且AiAi0=Ai+1Ai+10,CiCi0=Ci+1Ci+10,EiEi0=Ei+1Ei+10。

设OiP=Oi+1P=R0，AiOi=CiOi=EiOi=r，结合上述的长度和位置关系可解得：

(11)

由式(11)可以推导出摆转角αi和方位角βi与3根绳长度的变化量ΔLAi,ΔLCi,ΔLEi之间的关系为：

(12)

式(12)即为单个摆转关节的关节空间到驱动空间的运动学关系式。根据式(12)可以解得单个摆转关节的关节空间与驱动空间的映射关系为：

(13)

式(13)即为摆转关节单关节的驱动空间到关节空间的运动学关系。

2.1.3 串联摆转关节的运动学建模

分析摆转关节串联体的驱动空间与关节空间的映射关系时，使用3根绳子驱动整个串联摆转关节，当驱动所在的地方发生弯曲行为时必然会影响末端关节驱动线的长度，需考虑关节与关节间的耦合影响。摆转关节i发生弯曲时，关节i+1会随着关节i的摆转角αi和方位角βi的变化而变化。此时各个驱动线的变化量可分别表示为：

(14)

对各模块进行解耦合，解耦合后串联摆转体驱动绳长度变化量为：

(15)

式中n为串联的摆转关节的数量。

式(15)就是摆转关节串联体的关节空间到驱动空间的运动学分析。

2.2 折叠式柔性复合关节运动学建模

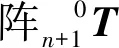
(16)

式(16)即表示了折叠柔性复合关节关节空间与操作空间的正运动学关系。

设坐标系Oi-XiYiZi各轴上的单位矢量为n,o,a；动坐标系Oi+1到定坐标系原点Oi的位置矢量用p表示。

现已知第4个摆转关节动平台On+1相对于扭转关节定坐标系O0的位姿，则矢量n,o,a,p对应坐标系O0-X0Y0Z0的矩阵为：

(17)

将式(16)和式(17)联立可以求得操作空间到关节空间的逆运动学分析关系式。

由于串联后的扭转关节与摆转关节串联体的驱动是相互独立的，故折叠式柔性复合关节关节空间到驱动空间的运动学关系为：

(18)

折叠式柔性复合关节的驱动空间到关节空间的运动学关系可由式(18)求得。

3 折叠式柔性复合关节运动仿真

通过软件对可折叠柔性复合关节进行仿真，在绳驱动的作用下，折纸关节可以做出伸缩或弯曲等动作。在仿真过程中使用的相关参数为：r=20 mm,l0=10 mm。在初始状态时，机构的扭转角、摆转角、方位角及驱动线的变化量都是0，扭转角范围为φ∈[0,π/3]，摆转角范围为α∈[0,π/3]和方位角范围为β∈[0,2π]。

将扭转关节驱动绳长度公式(6)在MATLAB中编程，输出扭转关节驱动绳长与扭转角的变化关系如图14所示。

图14 扭转关节的驱动绳长与扭转关节扭转角关系曲线Figure 14 Relation curve between drive line length and torsion angle of torsion joint

通过控制驱动绳变化量可以控制摆转关节的动平台上动坐标系原点的运动轨迹，并实现摆转关节不同的弯曲形态。单个摆转关节摆转过程中摆转角α∈[0,π/3]，方位角β∈[0,2π]，令采样次数s=180，相邻采样点间Δα=π/540,Δβ=π/90。根据文中提出的折叠柔性复合关节运动学分析模型，在MATLAB中编程，得到摆转关节动坐标系运动轨迹如图15～16所示。图15所示为单个摆转关节做摆转运动时动平台上动坐标系运动轨迹曲线。图16所示为单个摆转体在按图15中的轨迹做摆转运动时3条驱动绳长度变化曲线。

图15 单个摆转关节动坐标系运动轨迹Figure 15 Motion trajectory of single swing joint in moving coordinate system

图16 单个摆转关节摆转过程驱动绳长度变化曲线Figure 16 Variation curves of drive line length of single swing joint during swing

类似的我们也可以根据式(16)和式(18)将扭转关节与多个摆转关节串联(文中以3个摆转关节和1个扭转关节串联为例)后得到折叠式柔性复合关节的运动轨迹曲线与相应驱动绳长变化的关系，如图17和18所示。

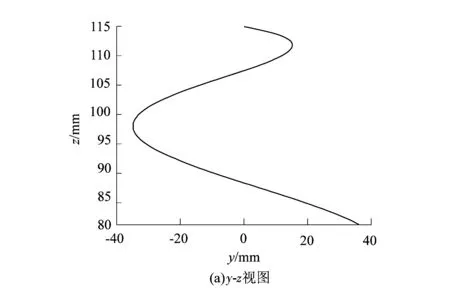
图17 折叠式柔性复合关节末端动坐标系运动轨迹Figure 17 Motion trajectories of end of folding flexible composite joint in moving coordinate system

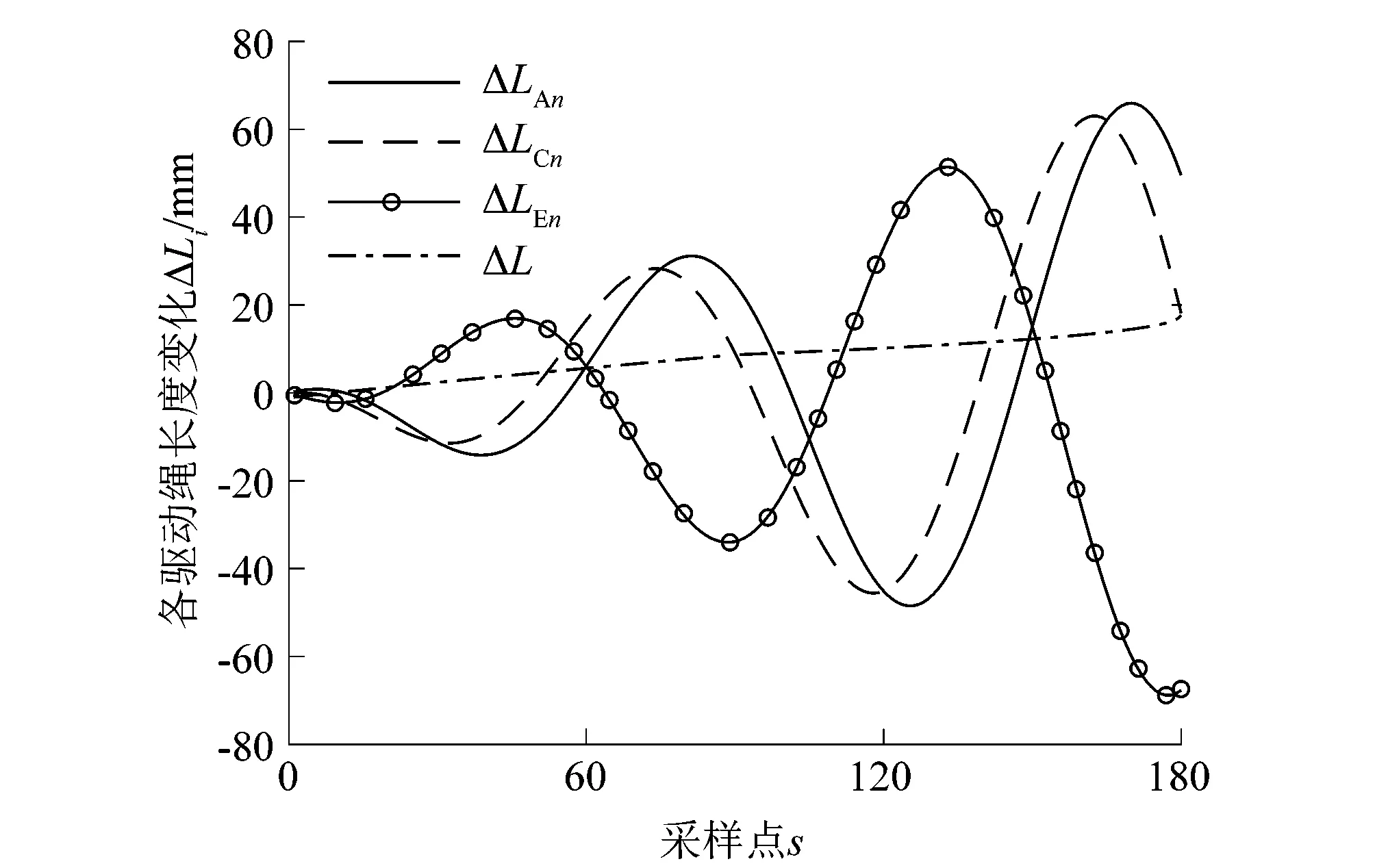
图18 折叠式柔性复合关节转过程驱动绳长度变化曲线Figure 18 Change curves of driving line length during rotation of folding flexible composite joint

折叠式柔性复合关节的工作空间可以利用式(16)确定折叠式柔性复合关节末端动坐标系原点O4的空间位置分布，利用MATLAB绘制其工作空间如图19所示。

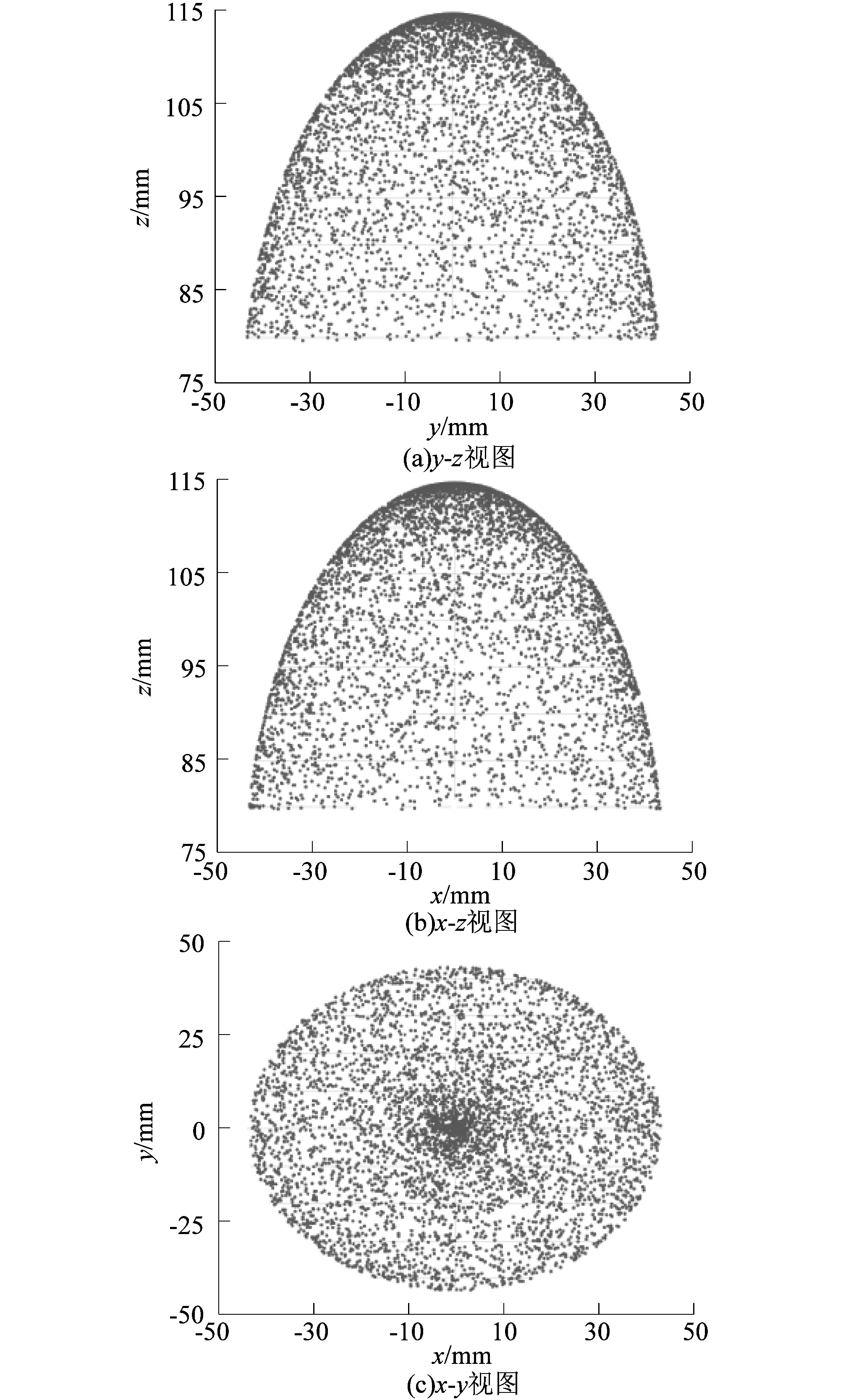
图19 折叠式柔性复合关节的工作空间散点图Figure 19 Workspace scatter diagram of folding flexible composite joint

4 结论

课题组利用折纸的可折展性与柔顺性，设计了多种折纸关节及多个关节串联成的折叠式柔性复合关节。主要研究成果如下：

1)基于折纸原理提出了折叠式扭转关节和折叠式摆转关节的设计方案，为后续折叠关节构型的研究与实际应用提供素材。

2)对折叠式扭转关节和折叠式摆转关节进行了运动学建模，分析了驱动空间-关节空间-操作空间的映射关系。

3)提出折叠式柔性复合关节的设计方案并建立驱动空间-关节空间-操作空间的运动学模型。

4)仿真验证了折叠式扭转关节、摆转关节的驱动空间-关节空间的理论数学模型的正确性；仿真并输出了折叠式柔性复合关节末端动平台坐标系原点的运动轨迹曲线及相应驱动绳长度变换关系并给出了工作空间散点图。