伺服绞织综框驱动机构优化

徐子晗，周香琴

(1.浙江理工大学 浙江省现代纺织装备技术重点实验室，浙江 杭州 310018；2.万利纺织机械研究院，浙江 杭州 311243)

绞织开口机构是纱罗织机上的重要组成部件，其作用是带动经纱做绞织开口运动。目前实现经纱绞织开口的方法有2种：绞综式和针排式[1]。其中，针排式绞织开口机构具有结构简单、寿命长、可靠性高及维护操作方便等优点，在纱罗组织的织造中应用较广，但品种适应性受限制。随着织造速度的提高，针排的运动规律对断经的影响尤显重要，特别在玻纤绞织行业，减少经纱与针排的摩擦、挤压，合理分配针排的纵向运动与横向运动的时间，对减少断经[2]，提高织机的速度具有重要的意义。

近年来，已经有很多学者对开口机构做过深入的研究，如织机开口机构的创新设计研究[3]，旋转变速机构运动规律对开口机构传动影响的研究[4]，开口机构惯性载荷特性研究[5]，开口引起的经纱张力变化规律研究[6]，开口机构的运动学和动力学研究[7-9]，及电子开口机构研究[10]等，但对绞织开口机构的研究较少。课题组针对针排式伺服绞织综框驱动机构进行运动学分析，建立针排运动规律分析模型，对机构结构进行优化，并利用组合三角函数对伺服电机运动规律进行设计，解决织造工艺和钢针对经纱摩擦的问题，为今后绞织开口机构的设计和性能优化提供了参考。

1 纱罗组织的结构特征及绞织过程

纱罗组织结构如图1所示，2组经纱G和S组成了经面，在一个织造循环周期内，与纬纱交织时，G经纱始终处于下层经纱位置，S经纱始终处于上层经纱位置，完成扭绞后G经纱与S经纱左右位置发生互换。

图1 纱罗组织结构Figure 1 Leno structure

纱罗织机种类繁多，其中一款针排式纱罗织机上机示意图如图2所示，经纱2从织轴1上送出，绕过固定后梁3，穿过停经片4后，分为S经纱和G经纱，其中S经纱穿入下针排7，G经纱绕过活动后梁5后穿入上针排6，与纬纱交织后形成织物，通过卷取辊8，卷绕到卷布辊9上。

1—织轴；2—经纱；3—固定后梁；4—停经片；5—活动后梁；6—上针排；7—下针排；8—卷取辊；9—卷布辊。图2 纱罗织机经纱上机示意图Figure 2 Schematic diagram of warp loading on leno loom

与传统织机不同的是：该绞织开口机构的执行构件为上、下两针排，上针排不运动，下针排既做上下运动，又做横向运动。绞织开口过程如图3所示，从开口1到开口2的过程中，上针排不动，下针排向下运动的同时向右运动(如图3(a))，当下针排运动到图3(b)所示位置时，S经纱到达最底端，然后下针排向上运动的同时向右运动(如图3(c))，最终S经纱从G经纱的左侧运动到了右侧，完成1次开口；下一次开口过程中，经纱S下降与上升的同时，从G经纱的右侧运动到左侧，完成绞织的一个循环。

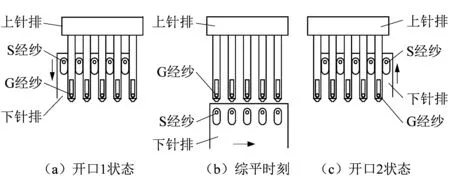
图3 绞织开口过程示意图Figure 3 Schematic diagram of twisting shedding process

2 伺服绞织综框驱动机构介绍

图2所示的纱罗织机中伺服绞织综框驱动机构简图如图4所示。正常织造时，主轴带动共轭凸轮10顺时针匀速转动，通过由共轭凸轮10、滚轮11和摆杆12组成的凸轮摆杆机构带动摆杆12绕转动中心B摆动，由提综臂13、送杆14和摇杆15组成的四连杆机构带动摇杆15绕中心C摆动，通过由传动杆16、撑杆17和下针排组成的曲柄滑块机构带动下针排做纵向运动，同时伺服电机带动偏心盘18逆时针匀速转动，通过连杆19带动下针排做横向运动，最终由下针排纵向运动与横向运动的相互配合，带动经纱S运动，与经纱G形成绞织开口。

以O点为坐标原点，针排横向运动方向为x轴方向，建立Oxy坐标系，点O(x1,y1)，B(x1,y1)，C(x1,y1)，Z(x1,y1)在坐标系的坐标分别是(0,0)，(201,107)，(1 123,-45)，(1 310,476)。该机构为双自由度双驱动机构，滚轮半径R=65.0 mm，若以下针排在最底端位置时刻为织机的开口0°位置，当针排在最底端时，主凸轮的最高点与E点处的滚轮接触，副凸轮的最低点与F点处的滚轮接触，偏心盘18的偏心距L2=2.1 mm，初始位置由λ1(含义见图5)确定，各机构参数含义见图5，相关参数如表1所示。

7—下针排；10—共轭凸轮；11—滚轮；12—摆杆；13—提综臂；14—送杆；15—摇杆；16—传动杆；17—撑杆；18—偏心盘；19—连杆。图4 伺服绞织综框驱动机构简图Figure 4 Schematic diagram of drive mechanism of servo heald frame

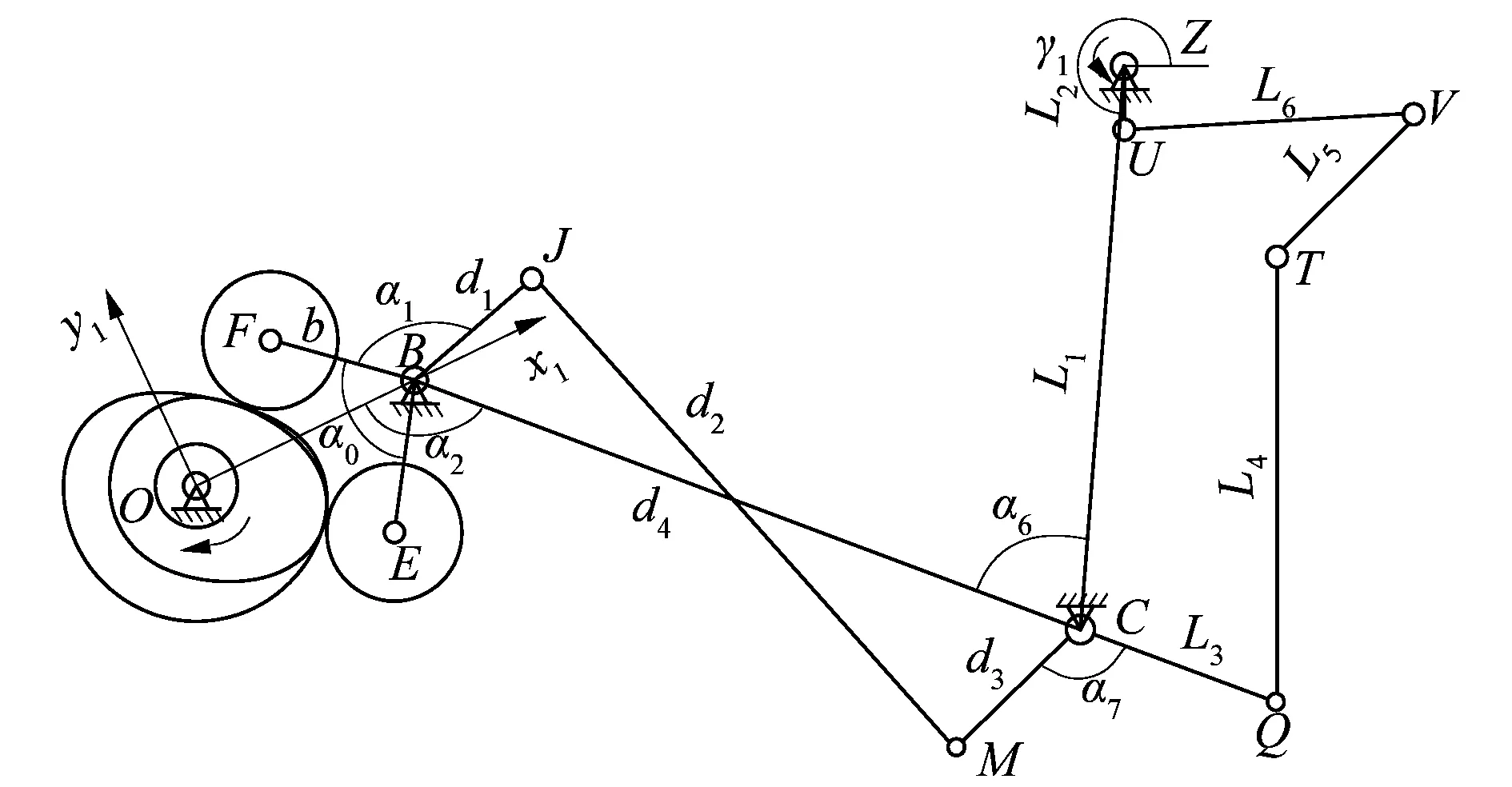
图5 绞织开口机构示意图Figure 5 Schematic diagram of twisted shedding mechanism

表1 机构初始参数Table 1 Initial parameters of mechanism

3 机构运动分析

以λ表示凸轮的运动位置(即主轴转角)，Δφ2表示伺服电机的转角开展机构运动学分析。

3.1 凸轮摆杆机构运动分析

3.1.1 凸轮理论廓线分析

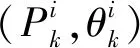
图6 求凸轮理论廓线Figure 6 Theoretical cam profile

根据图6建立矢量方程：

(1)

矢量方程(1)对x0轴、y0轴投影，可得：

(2)

根据式(2)求得矢量OEi的向径和向径角分别为：

(3)

3.1.2 凸轮摆杆运动规律分析

如图7所示，以O点为坐标原点，以OB0为x1轴建立Ox1y1坐标系。

图7 摆杆运动规律Figure 7 Movement law of pendulum

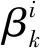
(4)

机架从OB0位置到达OBi位置的位置角λi为：

(5)

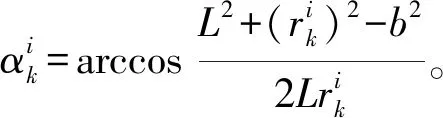
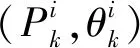
3.2 四连杆机构运动分析

绞织开口机构中的BJMC为平面四连杆机构，如图8所示，以B点为坐标原点，以BC为x2轴建立Bx2y2坐标系，在Bx2y2坐标系下建立矢量方程：

图8 四连杆机构简图Figure 8 Schematic diagram of four-bar linkage

BJ+JM=BC+CM。

(6)

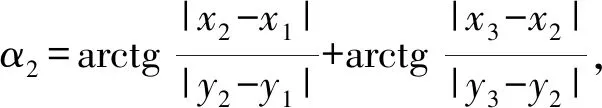
矢量方程(6)对x2，y2轴投影，可得：

(7)

由式(7)解得：

(8)

其中，遥杆CM在第4象限，式(8)取负号，

假设α5的计算过程函数为：

3.3 六连杆滑块机构运动分析

绞织开口机构中的CQTVUZ构成了一个六连杆滑块机构，为了分析方便，以Z点为坐标原点，以ZC为x3轴建立Zx3y3坐标系，如图9所示。

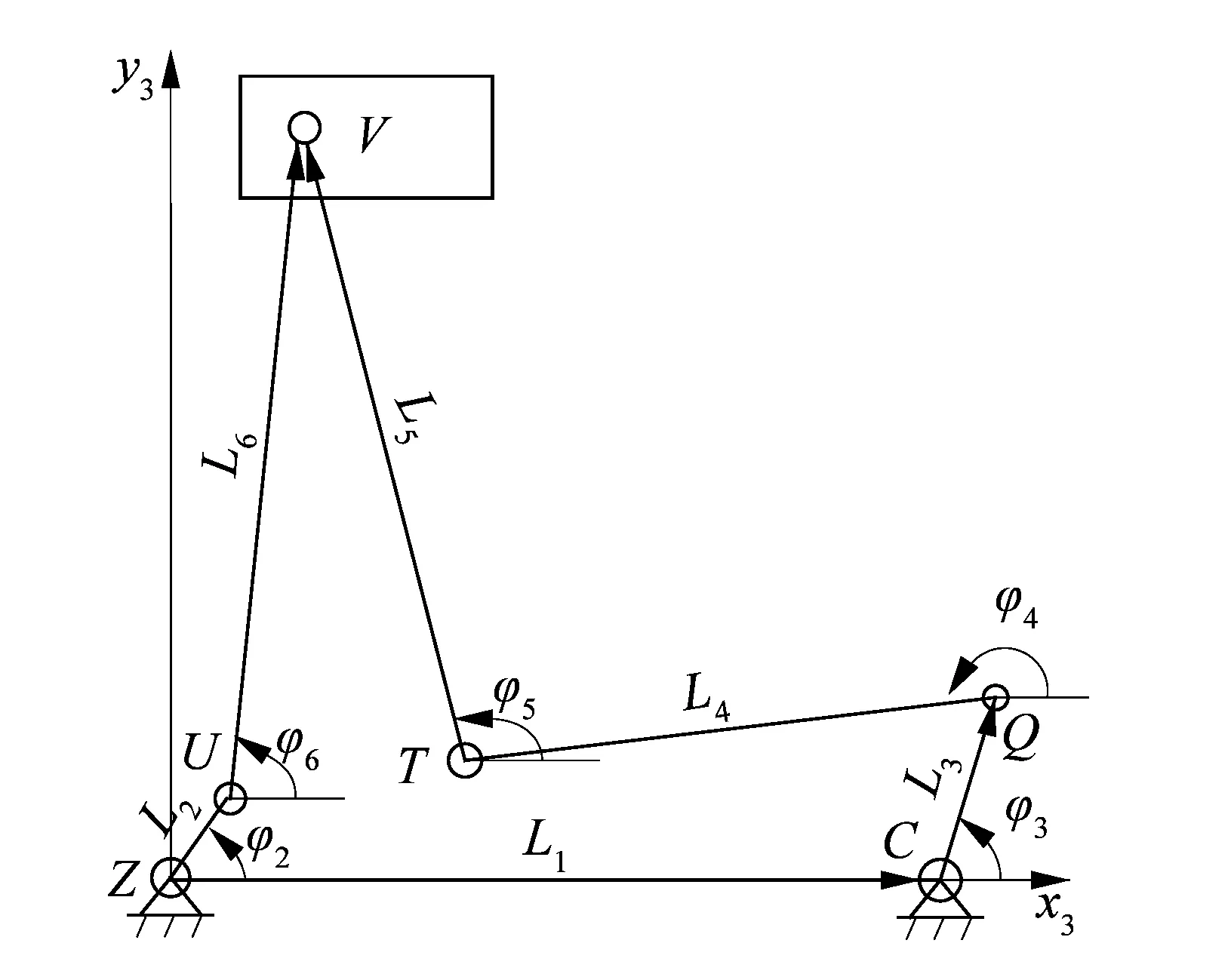
图9 六连杆滑块机构简图Figure 9 Schematic diagram of six-bar linkage slider mechanism

建立矢量方程：

ZC+CQ+QT+TV=ZU+UV。

(9)

由图5可知：

φ3=α5+α6+α7-360°。

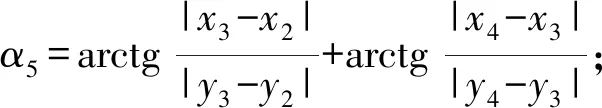
α6∈(0,π)。

矢量方程(9)对x3，y3轴投影，可得：

(10)

式中：L1，φ1，L2φ2，L3，φ3，L4，φ4，L5，φ5，L6和φ6分别为矢量ZC,ZU,CQ,QT,TV,UV的模和幅角；φ1=0；φ2为电机轴转角，且

根据式(10)运用MATLAB软件计算出φ4与φ6，求解函数如下：

[φ4,φ6]=solve (L1cosφ1+L3cosφ3+L4cosφ4+L5cosφ5-L2cosφ2-L6cosφ6,L1sinφ1+L3sinφ3+L4sinφ4+L5sinφ5-L2sinφ2-L6sinφ6)。

(11)

3.4 综框运动规律分析

以C点为坐标原点，建立Cxy坐标系，平行于Oxy坐标系，如图10所示。

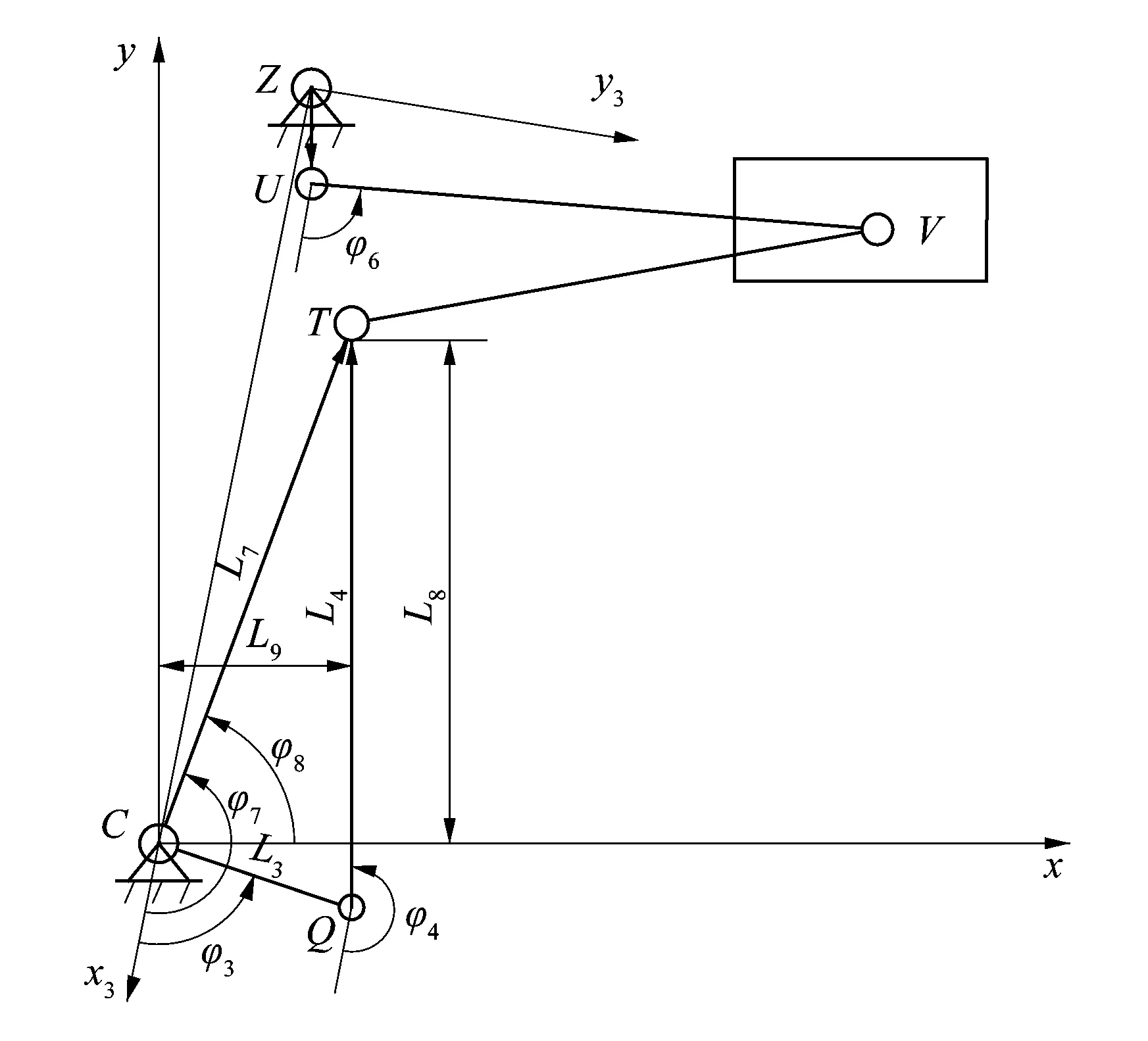
图10 下针排位移简图Figure 10 Schematic diagram of lower needle row displacement

矢量CT在Zx3y3坐标系下的模和幅角分别为：

(12)

如图10所示，矢量CT在y轴上的投影L8即为下针排的纵向位移，在x轴上的投影L9即为下针排的横向位移，且有

(13)

假设下针排纵向位移的计算过程函数为：

则下针排纵向位移的动程为：

(14)

假设下针排横向位移的计算过程函数为：

则下针排横向位移的动程为：

(15)

3.5 综框运动规律验证

利用Pro/E软件建立三维模型，如图11所示。并进行运动仿真，设定主轴转速为300 r/min，伺服电机轴转速为150 r/min，运行时间为0.4 s。得到下针排纵向仿真曲线S1和横向仿真曲线S2，将仿真结果与理论计算结果进行对比，结果如图12所示。从图12可看出，仿真结果与理论计算结果相吻合。

图11 绞织开口机构三维模型Figure 11 Three-dimensional model of weaving shedding mechanism

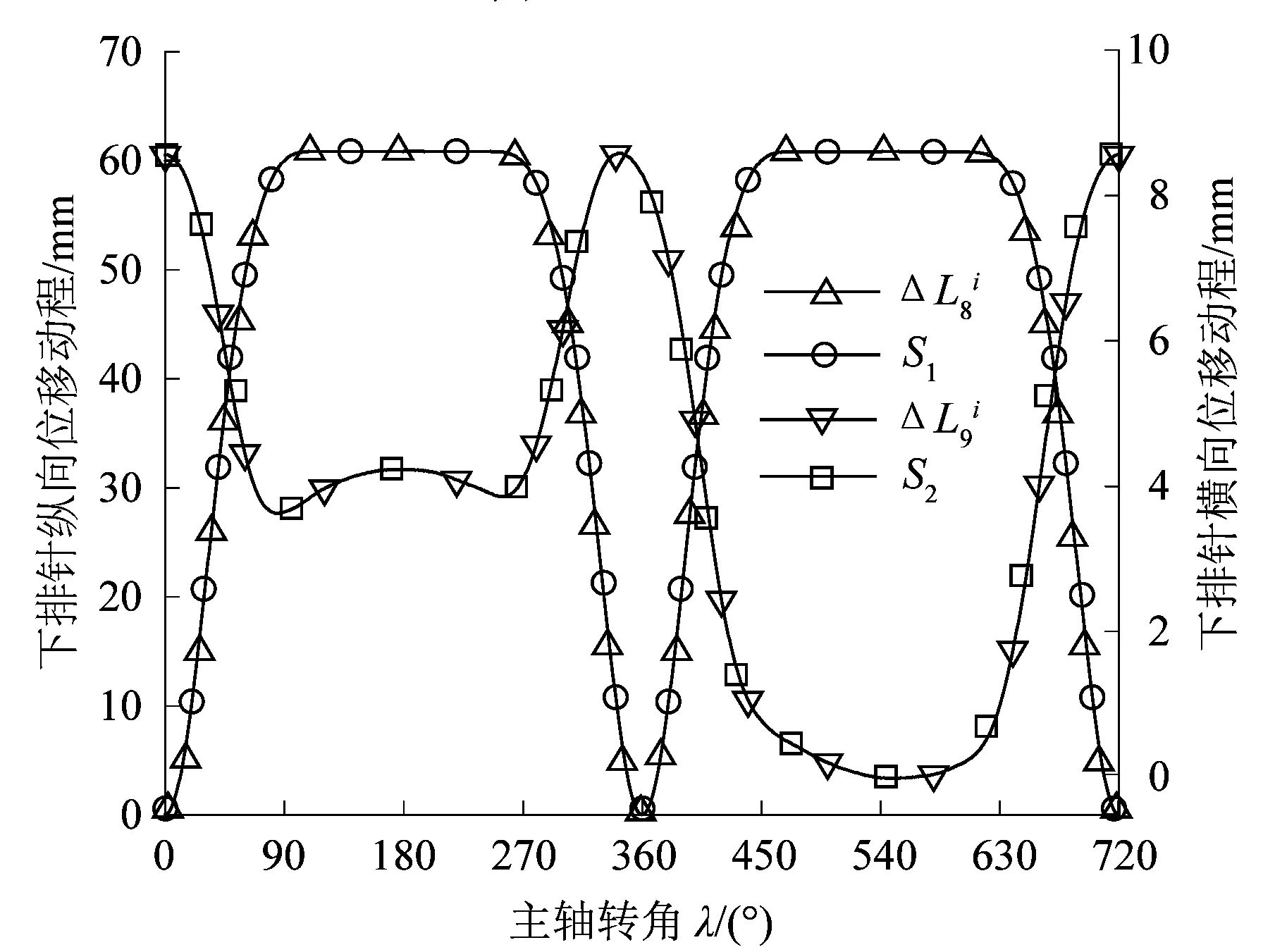
图12 下针排运动规律Figure 12 Movement law of lower needle row

4 机构参数分析与优化

4.1 偏心盘起始位置对综框运动规律的影响

当共轭凸轮起始位置不变，改变偏心盘起始位置时，由Pro/E导出下针排运动规律曲线。当λ1为270°，0°，90°，180°时得到下针排的纵向运动规律曲线S1，S1-1，S1-2，S1-3和横向运动规律曲线S2，S2-1，S2-2，S2-3，如图13和14所示。

图13 下针排纵向运动规律曲线Figure 13 Curve of longitudinal movement law of lower needle row

图14 下针排横向运动规律曲线Figure 14 Curves of lateral movement law of lower needle row

从图13～14中看出，主轴转角对纵向位移没有影响，但对横向位移影响较明显，并且存在2个问题：

1)下针排横向位移的极值位置不统一。

2)在1个开口周期内，下针排横向都迅速地来回了1次。

上述问题都不符合织造工艺要求，因此需要对该机构进行优化。

4.2 综框理想运动规律

下针排理想的运动规律，应是在2个开口周期内，横向来回1次，并且下针排在带动经纱的运动过程中不与上针排的钢针接触，理想运动规律如图15所示。S3，S4分别为下针排理想的纵向与横向运动规律曲线。

图15 下针排理想运动规律曲线Figure 15 Curves of ideal movement law of lower needle row

4.3 机构优化

4.3.1 机构的优化设计

根据下针排理想的运动规律，需要分离纵向与横向运动，设计出的机构如图16所示。

7—下针排；10—共轭凸轮；11—滚轮；12—摆杆；13—提综臂；14—送杆；15—摇杆；16—传动杆；17a—新撑杆；18—偏心盘；19a—新连杆；20—传动滑块；21—小连杆；22—连接滑块。图16 优化后机构简图Figure 16 Schematic diagram of optimized mechanism

其中：新撑杆17a替代了原撑杆17，在新撑杆17a与下针排7之间新增了连接滑块22和小连杆21；新连杆19a替代了原连杆19，在新连杆19a与下针排7之间新增了传动滑块20。优化后的机构参数如表2所示。对优化后的机构在Pro/E中建模仿真，得到下针排的运动规律，如图17所示。S5，S6分别为机构优化后下针排的纵向与横向运动规律曲线。

表2 优化后机构参数Table 2 Optimized mechanism parameters mm

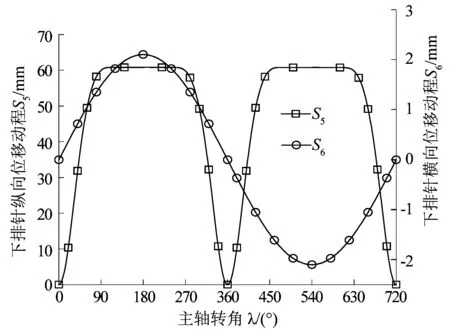
图17 优化后下针排运动规律曲线Figure 17 Curves of lower needle row movement law after optimization

根据机构优化后下针排的运动规律，得到下针排带动经纱运动的轨迹如图18所示。上针排上的钢针与经纱存在摩擦，使经纱容易出现断经的情况。根据图18中经纱S的运动轨迹，假设经纱S在针排中从D1位置开始运动，经过D2，D3，D4位置，到达D5位置，实现绞织的第1次开口，然后按原路返回，实现绞织的第2次开口。在第1次绞织开口周期内，D2位置为经纱S与钢针2开始接触位置，D3位置为经纱S与钢针2终止接触位置，经纱S与钢针2的接触长度为I1和I2，根据图17的运动规律可知，当开口动程为60 mm时，经纱与钢针的接触长度：I1=I2=38 mm。针对玻纤织物，经纱S与钢针接触着运动，特别是在经过D3位置时，玻纤经纱容易断经。因此针对不同的纱线，需要配合不同的伺服电机运动规律，以减少经纱与钢针的接触时间和接触距离。

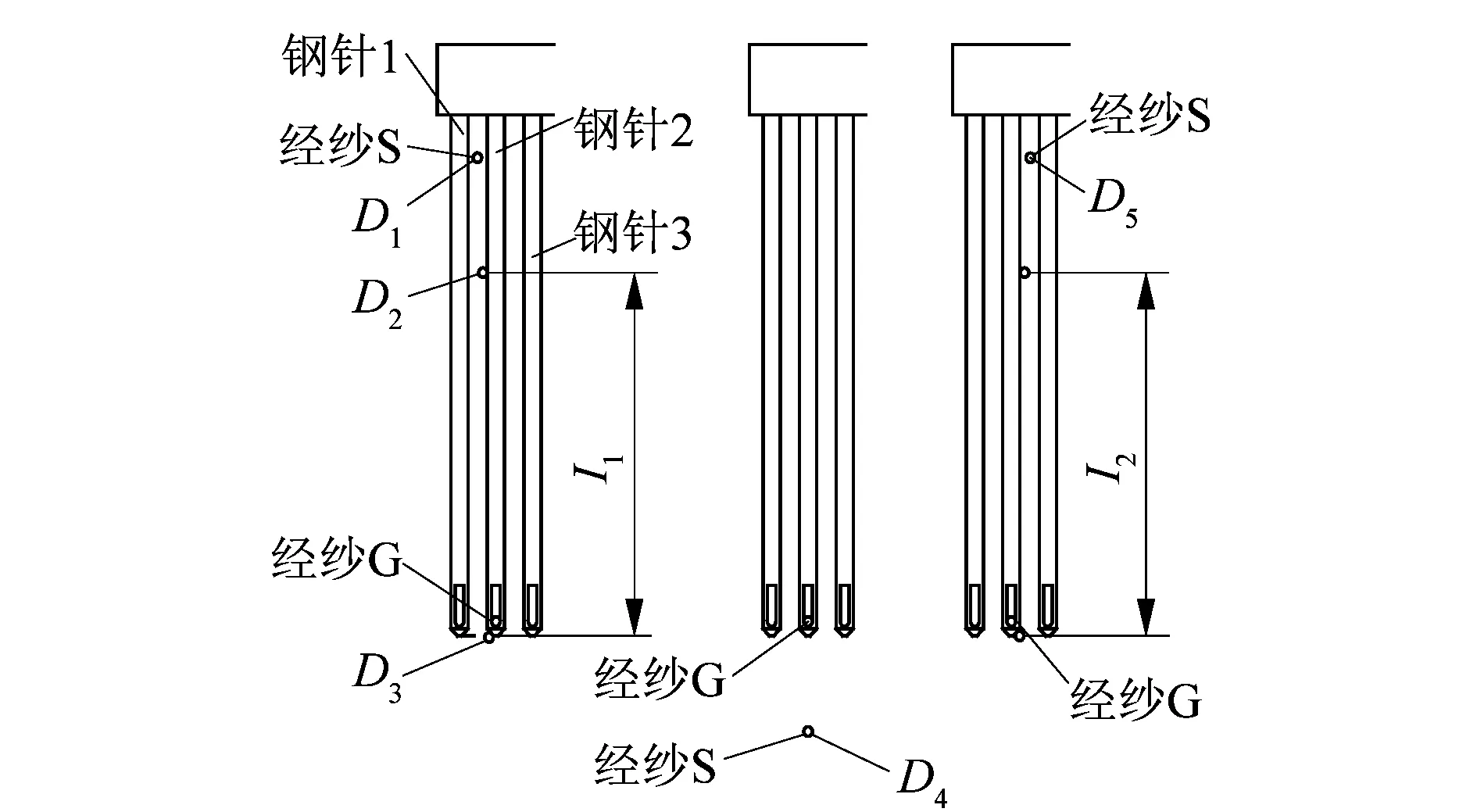
图18 经纱S运动轨迹Figure 18 Trajectory of warp yarn S

4.3.2 伺服电机运动规律设计

在不改变连接件尺寸的情况下，通过对伺服电机轴角位移的设计，改变下针排横向运动规律。根据图19所示的曲线组合方法，对伺服电机轴角加速度进行设计，假设λ=ωt，则角加速度a可表示为：

图19 伺服电机轴角加速度曲线Figure 19 Angular acceleration curve of servo motor shaft

(16)

式中：α，η，μ分别为a01，a12，a23段的转角系数；ω为主轴转速；A为伺服电机轴角加速度峰值。

对式(16)中的时间t积分，得到伺服电机轴角速度δ为：

(17)

对式(17)中的时间t积分，得到伺服电机轴角位移Δφ2为：

(18)

其中:

伺服电机运动规律设计参数如表3所示，将表3中的参数代入式(16)～(18)中，得到伺服电机运动规律如图20所示。图20中，Sa为伺服电机轴角加速度曲线，Sδ为伺服电机轴角速度曲线，Sφ为伺服电机轴角位移曲线，图中Sa，Sδ和Sφ以λ=270°为起始位置。

表3 伺服电机运动规律设计参数Table 3 Motion law design parameters of servo motor

图20 伺服电机运动规律曲线Figure 20 Movement law curves of servo motor

4.3.3 优化后综框运动规律分析

课题组按照优化后的绞织开口机构和伺服电机轴角位移曲线，在Pro/E中建模仿真，获得的下针排运动规律曲线与图15中的曲线相吻合。若下针排按照优化后的运动规律相互配合，则经纱S与钢针2的接触长度I1为0。因此下针排按照新的运动规律移动，既符合织造工艺要求，也能避免经纱与钢针的摩擦。

5 结论

课题组通过对伺服绞织综框驱动机构运动规律的分析，结合织造工艺要求，研究综框运动规律的合理性。

1)运用矢量法构建了伺服绞织综框驱动机构运动过程的数学模型，列出了综框动程求解方程。利用Pro/E软件建立了机构的三维模型，并进行运动仿真，结果显示仿真结果与理论结果相一致，验证了数学模型的正确性。

2)通过对偏心盘4个起始位置情况下的综框运动规律的分析可知：偏心盘起始位置对综框纵向运动没有影响，但对综框横向运动有较为显著地影响，并且都不符合织造工艺要求；同时提出了综框理想的运动规律曲线，可为机构的优化提供依据。

3)根据综框理想的运动规律，设计出了一种新机构构型，优化后的机构配合新设计的伺服电机运动规律克服了原机构的缺陷，在保证综框运动规律符合织造工艺要求的情况下，有效减少了断经，在实际应用中，可提高绞织物的质量和生产效率。