基于BSO-GA算法的机器人子区域覆盖路径规划
董雅文,杨静雯*,刘文慧,张宝锋
(1.西安工程大学 机电工程学院,陕西 西安 710048;2.西安理工大学 机械与精密仪器工程学院,陕西 西安 710048)
随着信息化、工业化的不断融合,机器人等智能化设备得到了越来越广泛的应用,路径规划作为机器人的关键技术之一,深刻影响着机器人的作业质量和作业效率。路径规划一般可分为传统点到点式路径规划以及全覆盖式路径规划。点到点路径规划是最常见、最基本的路径规划问题,它需要在作业空间中寻找从起点到终点的一条无碰撞最优或较优路径;全覆盖式路径规划则要求机器人在作业空间中寻找一条经过封闭区域中所有可达区域的路径,同时某些性能达到最优或较优。目前,全覆盖式路径规划已应用到了很多领域,如机器人清洁、喷涂、消毒、排雷和探伤检测等。
整体而言,与传统点到点路径规划问题相比,针对全覆盖式路径规划问题的研究相对较少,但近些年来全覆盖式路径规划逐渐成为研究热点。目前针对全覆盖式路径规划的研究主要集中在4个方面:①以神经网络作为切入点研究的全覆盖路径规划,如运用生物激励神经网络及各种改进算法[1-5]、具有长短期记忆层的卷积神经网络[6]等来规划覆盖路径;②基于区域分割的全覆盖路径规划,主要探讨子区域覆盖的路径规划、遍历顺序的确定和衔接路线规划问题;③从环境建模着手来提高全覆盖效率,如对栅格添加属性值[7]及运用正六边形栅格建模[8]等;④在机器人全覆盖行进过程中制定一系列规则及策略进而达到提高覆盖率、降低遗漏率的目的,如回溯机制[9]、分治思想[10]、阿基米德螺线走法[11]和沿边学习机制[12]等。其中,针对基于区域分割的全覆盖路径规划问题,周利坤等[13]运用区域分割法进行环境建模,各区域内部采用内螺旋法覆盖,最后以邻接矩阵和深度优先搜索(depth first search,DFS)确定油泥区的衔接顺序和最短路径,完成油泥区的覆盖。该方法能够以较高覆盖率和较低重复率来完成油泥区的覆盖任务,但各子区域内部采用内螺旋法覆盖,在面对不规则的分区环境时,会产生较多冗余路径。马全坤等[14]在用矩形分割创建环境模型后,通过记忆模拟退火算法搜索出任务最优目标点行走顺序,然后使用A*算法进行跨区域衔接路径规划。研究结果表明,重复率控制在4.2%左右,且遍历路径规划能够达到100%;但在子区域内部行走陷入死区时,往复式覆盖并不能有效逃离。李楷[15]针对子区域存在锯齿形障碍物的情况提出了起始点方向优先(starting point direction first,SPDF)局部区域覆盖方法,研究结果表明,与局部区域覆盖(boustrophedon cellular decomposition,BCD)算法相比,SPDF局部区域覆盖算法首次覆盖百分比平均值提高了近20%;但当环境出现多种类型障碍物时,该方法不能有效应对。张赤斌等[16]采用Boustrophedon分解进行区域分割,各子区域内部采用往复式覆盖,利用蚁群算法进行区域遍历顺序优化,研究结果表明,遍历顺序对全覆盖效率有着重要的影响,但该方法并不能达到100%覆盖的效果。唐东林等[17]运用矩形分割法创建环境模型,将往复式覆盖与路径选择函数相结合,研究结果表明此方法能够有效逃离死区,但不能有效规划凹形障碍物周围覆盖路径。郭典新等[18]针对割草机器人全覆盖路径规划问题,在完成单元分割创建环境模型后,采用改进的往复式和回行式覆盖,依据地块形状规划其覆盖路径,研究结果表明该方法能有效减少重、漏作业现象,但该方法并未考虑障碍物较为复杂的情况。
目前,基于区域分割的全覆盖路径规划的研究较多文献仍采用传统方法来规划区域内部覆盖路径,而传统方法对环境普遍适应性较差。课题组在完成环境建模和区域分割后,采用头脑风暴-遗传融合算法(brain storm optimization -genetic algorithm,BSO-GA)对子区域内部进行全覆盖路径规划。利用优化算法规划全覆盖路径,一定程度上避免现有方法适应性不强的问题;同时BSO算法中引入GA变异操作的思想,能够提高算法的随机性和收敛速度,使其能够较好地完成作业。
1 环境建模
1.1 建立栅格地图
课题组运用栅格法创建作业环境模型,栅格大小由机器人作业范围决定。每个栅格包含3种状态:空闲、完全占据和部分占据。对于完全或部分被障碍物占据的栅格都视为障碍区域;对于完全处于空闲状态的栅格视为自由区域。
1.2 区域分割
区域分割是将复杂的作业环境依据障碍物的分布情况划分为多个子区域,使得各子区域内部不再包含障碍物。这种化整为零的思想在很大程度上降低了机器人全覆盖路径规划的实现难度。区域划分与后续子区域覆盖规划的优劣也有着密切联系。课题组采用莫尔斯分解[19]对作业区域进行划分,它不仅能够处理多边形障碍物的环境划分,而且分解完成之后的子区域较少,可以减少机器人路径冗余,进而降低能耗、节省时间。
莫尔斯分解是一种基于临界点分析的精确单元分割法,通过构造莫尔斯函数进行切片扫描来划分区域。莫尔斯函数是定义在k维空间的可导函数。对于一个莫尔斯函数h:Rk→R,其在任一点p的一阶导数为:
(1)
当在此空间中的任意一点p0满足以下条件时:
(2)
则称p0为临界点。
切片是根据确定的莫尔斯函数定义的一个覆盖空间的余维数流形[20],其形状取决于所选的莫尔斯函数,并能够产生不同的单元分割形式。当切片扫过目标区域遇到障碍物时,会把空间区域分割成更小的切片。当切片离开障碍物时,一些小切片会聚合起来。这些区域聚合性发生变化的点是障碍物的临界点。莫尔斯函数依据作业环境灵活选取。
2 算法设计
子区域内部覆盖路径规划常用的方法是往复式覆盖法和螺旋式覆盖法,但这类方法在环境中存在锯齿形、凹形障碍物以及起始点不固定等情况时,不能做出有效应对。针对上述问题,课题组采用优化算法来完成子区域内部的覆盖,使其在一般和特殊环境下都可以有效完成作业。课题组以各栅格中心点为目标,机器人成功遍历各中心点至少一次则代表完成该栅格的覆盖。考虑到遍历点数过多,依据区域划分结果对各目标点进行分组,这样能够很大程度上缩小搜索空间,进而将此问题转化为旅行商问题进行求解。旅行商求解的最短路径即为子区域内部的较优路径。
2.1 头脑风暴(BSO)算法
头脑风暴优化(brain storm optimization,BSO)算法由SHI[21]于2011年提出,其主要思想源于多人集思广益商讨并解决问题。BSO算法根据头脑风暴的过程引出了4个操作过程,即初始化全部个体、聚类、新想法生成和想法选择,主要步骤有6个。
1)初始化参数及全部想法。在BSO中将独立个体称为想法,首先模拟头脑风暴过程中每一轮产生N个想法。
2)对N个想法进行适应度值评价。
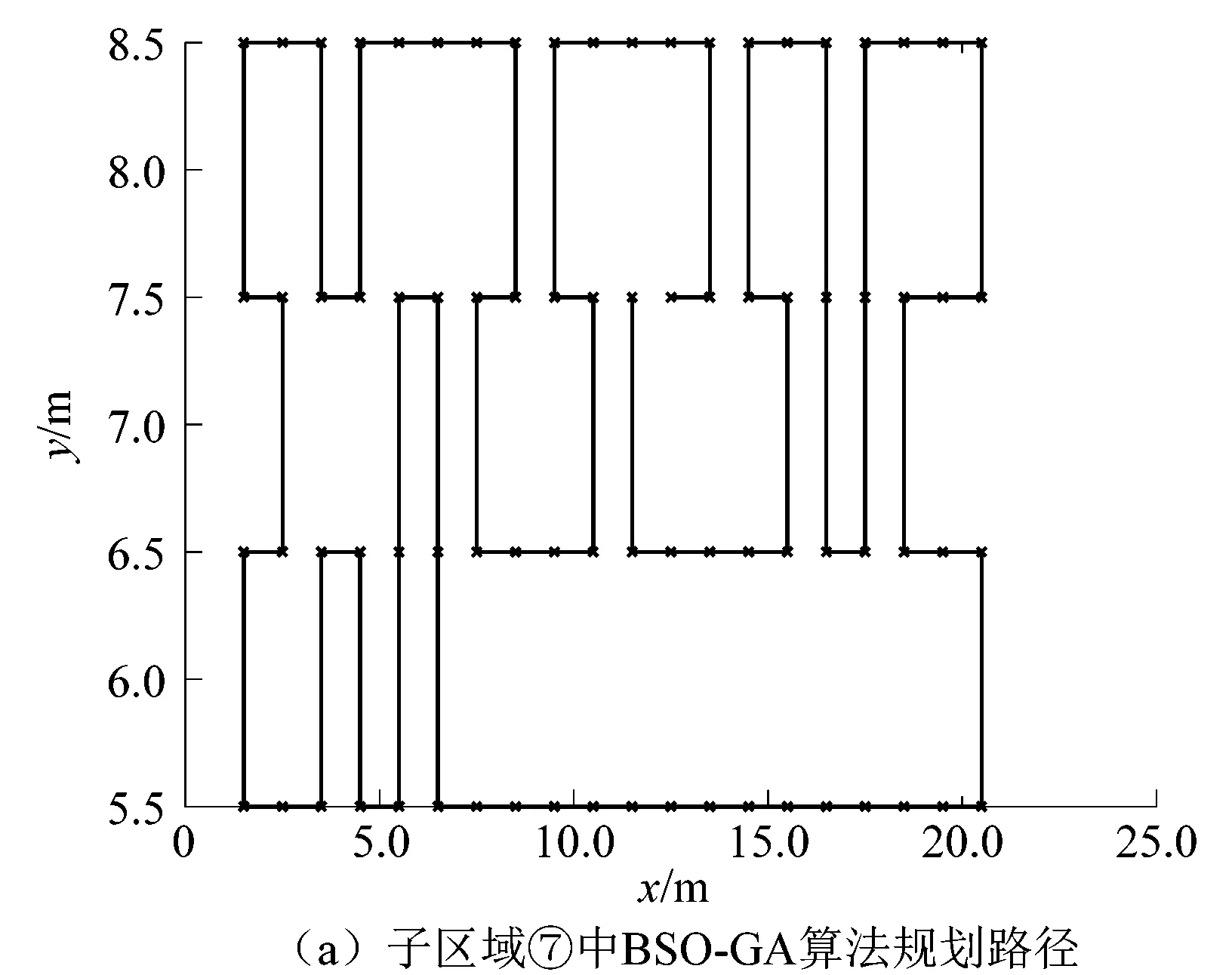
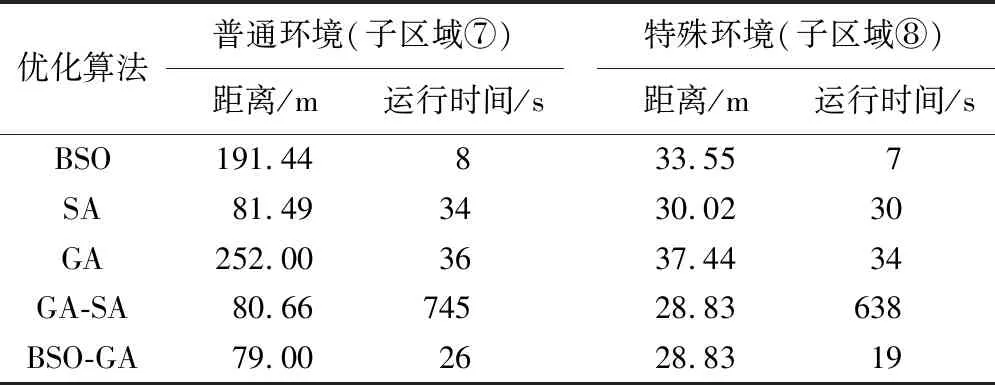
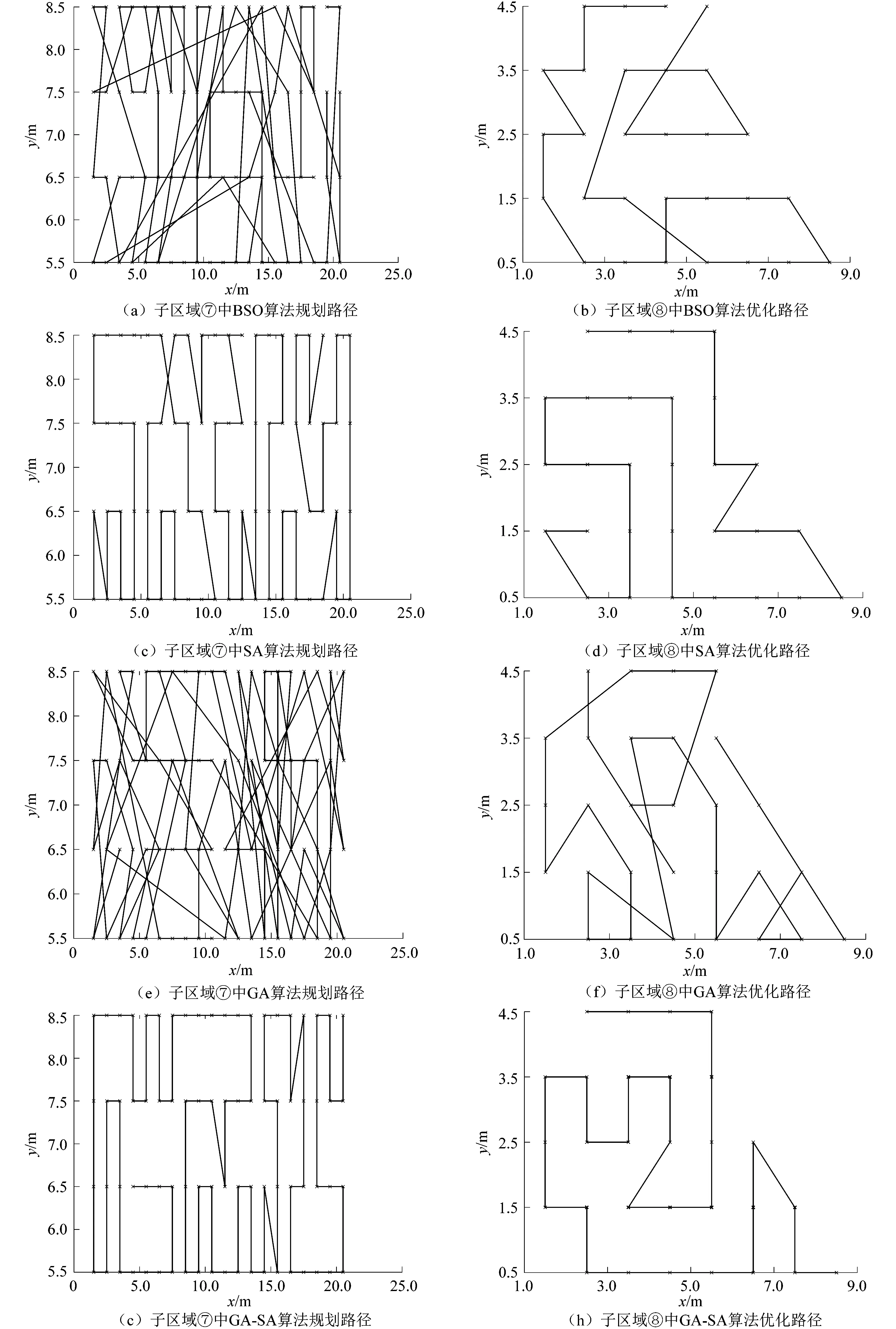
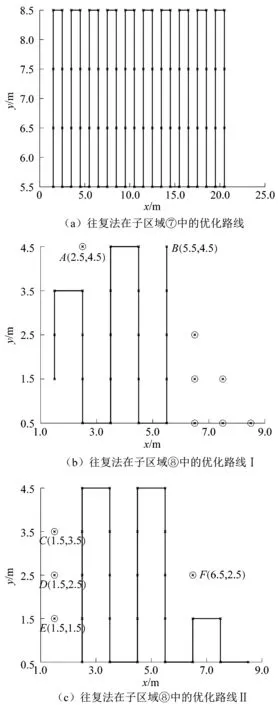
3)对N个想法进行聚类。通过聚类算法将其划分为M组,通过排序的方式选出最优想法(组中心个体)。为保持种群多样性,生成随机数r1∈(0,1),若r1 4)产生新想法为BSO的核心部分。产生新想法主要有2个阶段,即选择和更新。 第1阶段为选择。首先按照概率值pb先选择基于1组或2组产生新想法;其次按照概率值pc,pd再选择是基于组中心还是基于组内随机个体产生新想法。具体过程为:①生成随机数r2∈(0,1),若r2 第2阶段为更新,更新想法的方式有2种: ①选择1个想法(组中心想法或组内随机想法)作为Xs,对Xs进行扰动生成新想法,则有 (3) (4) 式中:itermax为最大迭代次数;iternow为当前迭代次数;k用来控制logsig函数的变化速率;rrand为服从(0,1)均匀分布的随机数。 ②选择2个想法(2个组中心想法或2个组内随机想法)作Xs1,Xs2混合可得: (5) 6)若达到设定的最大迭代次数,则输出结果;若还未达到,则跳转至1)。 BSO算法与其他模仿生物遗传和觅食等群体行为的优化算法不同,它通过模拟人类交流沟通解决问题,能够在全局搜索和局部搜索之间达到较好的平衡,即采用数据分析将想法分组集合,组内搜索各自解空间中的局部最优解,然后经过组之间的交流沟通来得到全局最优解。同时,个体经更新操作进一步丰富了种群的多样性,这使其在求解优化问题中表现出了良好的性能。 BSO个体通过式(3)和式(5)进行更新的方式在解决本文问题时适用性不强,易陷入局部最优,收敛性较差。因此,课题组引入遗传算法(genetic algorithm,GA)对个体实施变异,即倒位、移位和换位产生子代的思想,将其作为BSO基于1个想法更新的方式,并借鉴文献[22]提出的改进交叉操作,采用基于2个想法的贪心交叉完成混合产生新想法,主要有6个步骤。 1)初始化BSO和GA算法参数及全部想法。如BSO种群数N、最大迭代次数Gmax、聚类数M和选择1个聚类概率、GA换位概率pe、移位概率ps和倒位概率pi等。接下来则按照种群数N随机生成初始想法。 2)适应度评价。对于本文中所要解决的全覆盖路径规划问题,只需机器人在子区域内行走路径最短即可。这里采用Euclidean距离表示行走路径长度L,适应度函数为: (6) 式中:n表示子区域内部需要遍历点的数量;(xi,yi)表示各点坐标。 3)对N个想法进行聚类。采用K-Means算法将其分为M组,根据pa判断组中心是否会被随机产生想法取代。 相关统计显示,急性肾衰伤的发生率在5%到20%左右,手术是引起急性肾衰伤的主要因素,其中心胸外科,心内科以及神经外科发生急性肾衰伤的概率相对较高,急性肾衰伤在临床中具有较高的病死率,通常病死率将超过30%[2] 。 4)产生新想法。第1阶段已在2.1节进行了相关说明,故此不再赘述。经选择后,对其进行更新。 在本研究中,解空间为解的所有排列顺序集合,可表示为: S={(s1,s2,…,sn)|(s1,s2,…,sn)为子区域内部需要遍历点(1,2,…,n)的循环排列}。 首先,生成随机数r5∈(0,1),将pe,ps,pi构成行向量,对其横向累加得到(pe,pe+ps,pe+ps+pi),分别判断r5与pe,pe+ps,pe+ps+pi的大小,找到首先满足“≥r5”关系的位置,若pe≥r5,执行交换算子;若pe+ps≥r5,执行移位算子;若pe+ps+pi≥r5,执行倒位算子。 其中:移位算子以概率ps随机将某子串中的个体依次向后(前)移位;倒位算子以概率pi随机将某子串中的个体依次倒位;换位算子以概率pe随机交换某位置的个体。 ②若Xs1,Xs2为组中心想法或组内随机想法,对Xs进行贪心交叉操作实现更新。 a)随机生成起点如a=s3,分别在Xs1,Xs2中搜寻s3的左邻,分别为s2,s4,根据{s3,s2},{s3,s4}距离大小决定下一点,若{s3,s2}距离小,则Xs11第2位为s2。 b)将s3从Xs1,Xs2中剔除,再次随机生成起始点b=s5,在Xs1,Xs2搜寻s5的左邻,为s6,s4,根据{s5,s6},{s5,s4}距离大小决定下一点,依此类推,直至Xs1中只剩下一个元素。此时,可以得到Xs11。 c)同理,通过搜寻右邻可以得到Xs22。 5)想法选择。生成新想法Xn后,若Xn比Xs适应度值更优,那么将其替换。 6)判断是否满足终止条件,若满足,迭代结束;否则,跳转至3)继续循环,直至满足条件为止。 通过莫尔斯分解将作业区域进行分割,然后运用BSO-GA算法完成子区域覆盖,为验证该方法的有效性,通过消毒机器人对门诊大厅进行作业来完成实验仿真。设定消毒机器人的作业范围为1 m×1 m,即栅格大小为1 m×1 m,门诊大厅面积为400 m2,那么栅格数为20×20。首先模拟作业环境进行环境建模,结果如图1(a)所示。 图1 环境建模Figure 1 Environment modeling 得出作业环境栅格模型后,依据环境模型特点,选取莫尔斯函数为直线簇{yp=ypi|ypi∈[0,20]}对作业区域进行扫描,以区域④~⑥为例,现有4条直线Ⅰ~Ⅳ,如图1(b)所示Ⅰ和Ⅱ间的直线未被障碍物分割,因此,默认分段数为1,即Ⅰ和Ⅱ间区域为1个子区域;Ⅱ和Ⅲ间直线被分为3段,即Ⅱ和Ⅲ间区域被分割成3个子区域;Ⅲ和Ⅳ间直线分段数为1,自由区域的连通性发生了改变,可得临界点为两障碍物的8个顶点。因此,当直线Ⅰ扫过作业区域时,可得出Ⅱ和Ⅲ间有3个子区域,完成区域分割。同理可得经扫描后,共9个子区域,如图1(c)所示。 课题组利用BSO-GA算法规划子区域内部覆盖路径,而GA-SA融合算法由于模拟退火算法(simulated annealing,SA)的引入,能够在一定程度上改善GA陷入局部最优的缺陷。因此,将本文算法与BSO,GA,SA和GA-SA算法进行效果对比,以验证本文融合算法的有效性。现将各空闲栅格中心点看作目标点,对图1(c)中9个区域进行内部路径规划。以子区域⑦和⑧为例,分别运用往复法及优化算法BSO,GA,SA,GA-SA,BSO-GA在普通环境区域⑦和特殊环境区域⑧(存在锯齿障碍物、凹形障碍物)下进行全覆盖路径规划。实验环境为MATLAB R2016b,5种算法种群规模均设为50,迭代次数为1 000。SA算法的T0=0.025,α=0.99,内层循环次数为15;GA算法的pc=0.8,pm=0.2;BSO-GA相应参数设置如表1所示。 表1 BSO-GA算法参数设定Table 1 Parameters setting of BSO-GA algorithm 分别将子区域⑦和⑧局部放大并提取各中心点,运用BSO-GA算法进行路径规划,结果如图2所示。 由图2(a)和(c)可以看出,所有栅格(中心点)均覆盖,覆盖率为100%,且无路径重复及交叉现象。图2(b)在100代左右总距离收敛至79.00 m并趋于稳定,图2(d)在50代左右收敛至28.83 m并趋于稳定。并将其分别运行20次,总距离均能收敛至79.00和28.83 m,平均用时26和19 s。可以看出具有较强的稳定性及良好的全局收敛性。 图2 BSO-GA规划路径结果Figure 2 Path planning results of BSO-GA 再分别运用优化算法BSO,SA,GA和GA-SA对子区域⑦和⑧进行覆盖路径规划,结果如表2和图3所示。 表2 仿真结果Table 2 Simulation results 图3 其他优化算法规划路径结果Figure 3 Path planning results of other optimization algorithms 由图3、图4和表2可得,无论是在一般环境还是特殊环境下,GA-SA算法在BSO,SA,GA,GA-SA 这4种算法中表现较好,路径交叉及重复现象也比较少,但其运行时间是BSO-GA算法的近30倍;当覆盖面积较大时,BSO算法就显现出收敛性较差的缺陷,出现了大量如图3(a)所示的路径冗余,自然距离大大增加;覆盖面积较小时同样出现了如图3(b)所示路径交叉现象;而GA算法总距离随着迭代次数增加呈现阶梯式下降,在收敛前出现了如图4所示的2~3个平台期,说明其易陷入局部最优;由于SA算法每次循环仅对一个解实施扰动并更新,因此从图4(a)中可以看出,当覆盖面积较大时收敛速度较为缓慢。 图4 总迭代曲线Figure 4 Total iteration curve 运用传统往复法规划路径结果如图5所示。往复法默认上、下、左、右4个行驶方向为前进方向,由图5(a)可知,在一般环境中,该方法能够很好地完成覆盖任务,但由于环境存在凹形障碍物,图5(b)中出现了遗漏点A,并且机器人在行走至B时陷入死点(上、下、左、右均为已完成覆盖区域或障碍区域),由于未能有效脱困,从而导致了图5(b)右下方6个遗漏点;当从右边界开始往复覆盖时,同样由于存在锯齿形障碍物,出现图5(c)的遗漏点F,凹形障碍物内部的3个点C,D,E也为遗漏状态。由此可见,往复法在规划路径时,易出现遗漏及陷入死点的情况。综上,无论是与所列优化算法相比,还是与传统往复法相比,本文方法在解决子区域内部覆盖路径规划问题时表现较好且适应性较强。 图5 往复法规划路径结果Figure 5 Results of path planning by reciprocating method 现运用BSO-GA算法对所有区域进行路径规划,结果如图6所示,子区域①~⑨行走距离分别1.48,11.41,59.00,9.00,54.00,9.00,79.00,28.83和28.83 m;规划时间分别为12.3,11.0,30.7,9.7,30.2,9.8,26.0,19.0和12.2 s,将其累加得到整个区域行走距离共为280.55 m,时间共为160.9 s。由图6可知,本文方法所得路径没有交叉重复、遗漏及陷入死点的情况,在距离和时间上均占据优势,且覆盖率能够达到100%,可以较好的完成覆盖任务。 图6 各子区域内部覆盖路径Figure 6 Internal coverage path of sub-area 课题组针对基于区域分割的全覆盖路径规划问题进行了一定的探索,在完成环境建模及区域分割后,提出了BSO-GA算法,有效克服了传统方法存在的问题。结果表明,无论在普通还是特殊的作业环境中,与其他优化算法相比,BSO-GA算法在距离、运行时间上均占据一定优势,能够较好地完成覆盖作业。 相关有待深入研究的问题:①寻找精确度更高的环境建模及区域分割方法;②规划覆盖路径时将路线转角作为约束考虑,或同传统方法结合,进一步提高覆盖方法的效率;③以最短路径衔接各区域模块是下一步需要关注的问题;④由于优化算法的随机性导致最优路径一致性不大,因此,如何依据作业环境选取最满意路径也是需要关注的问题。
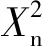
2.2 头脑风暴-遗传(BSO-GA)融合算法


3 基于BSO-GA算法的子区域覆盖路径规划仿真




4 结论

