基于绝对节点坐标法的超弹性材料二维梁单元动力学研究

郭嘉辉，赵春花，独亚平，周 川，张立强

(上海工程技术大学 机械与汽车工程学院，上海 201620)

随着科学技术的发展，橡胶等超弹性材料正逐渐应用于大变形柔性多体系统中，如轮胎、橡胶履带、橡胶输送带、软体夹持器和软体机器人等。橡胶作为一种典型的超弹性材料，其材料特性表现为变形能力大、回弹快、无迟滞性以及体积近似不可压缩等。超弹性材料具有非线性的应力与应变关系，相比传统的线弹性材料，同时会产生几何非线性和材料非线性的双重复杂特性，给大变形柔性多体系统的动力学仿真和力学特性分析提出了挑战。

Shabana提出的绝对节点坐标法(absolute nodal coordinate formulation，ANCF)是柔性多体系统动力学建模方法之一,单元节点广义坐标定义在全局坐标系下，使得单元质量矩阵为常数阵，且单元运动微分方程组装成系统总运动微分方程时，无需进行坐标转换，为其动力学模型求解以及复杂系统动力学建模提供了极大便利[1-3]。另外，该方法用位移梯度代替传统有限单元中的有限转动，并丢弃了各种假设，因此能模拟出柔性部件的真实变形，为处理大变形、大范围运动问题提供了可能。绝对节点坐标剪切梁单元位移模式通常采用多项式作为近似函数，那么多项式位移模式的选择是决定梁单元力学特性的关键。绝对节点坐标剪切梁单元首先提出的都是横向一次剪切梁单元，这些单元[4-9]的位移模式在纵向分量上都是高次插值，在横向分量上都是线性插值，因此又称为低阶梁单元。沈振兴等[10]和赵春花等[11]分别针对三维低阶梁单元和二维低阶梁单元，理论分析了线弹性材料的泊松闭锁问题，指出其主要原因是多项式位移模式横向一次和纵向高次不满足本构方程表达的纵横向应变之间关于泊松比的线性关系，导致低阶梁单元求解结果精度低。2010年以来，绝对节点坐标高阶梁单元即横向高次的剪切梁单元得到研究[12-16]。目前，已开发的高阶梁单元在原横向一次的基础上均只引入了横向二次多项式。因为横向二次多项式的存在，其位移模式具备了二次完全多项式，满足了本构方程表达的纵横向应变之间关于泊松比的线性关系，它们的精度被证明明显好于低阶梁单元。

目前，橡胶材料本构关系主要采用3种不可压缩模型：Neo-Hookean，Mooney-Rivlin和Yeoh。Maquedahe等[17]、Jung等[18]、Orzechowski等[19-20]和Xu等[21-22]采用绝对节点坐标三维低阶梁单元和三维高阶梁单元模拟橡胶梁的弯曲大变形，计算精度较高，但由于自由度较多，且非线性材料本身收敛迭代次数较多，导致计算时间较长，对计算机硬件有较高要求。目前，涉及二维绝对节点坐标剪切梁单元在超弹性材料非线性方面的力学特性研究较少。二维绝对节点坐标剪切梁单元的自由度数明显少于三维高阶梁单元。在可以转化为二维问题的情况下，使用二维绝对节点坐标剪切梁单元对提高计算效率具有很大益处。因此课题组基于绝对节点坐标高阶梁单元研究了大变形橡胶梁力学模型的计算精度和计算效率，探索了3种不可压缩超弹性模型(Neo-Hookean，Mooney-Rivlin和Yeoh)模拟橡胶梁大变形力学特性的有效性，以及单元自由度数对计算效率的影响。

1 二维绝对节点坐标横向高阶梁单元

绝对节点坐标法在绝对坐标系下假设单元内任意一点位置坐标的多项式位移场。目前存在3种二维绝对节点坐标横向高阶梁单元，分别由Patel等[16]2929和Zhao等[11]482提出。它们的多项式位移模式如表1所示。其中：ri为单元内任意一点的位置坐标，二维情况下，i=1,2；ai1～ai8为多项式位移模式的未知系数。利用节点广义坐标，推导得到单元形函数，这样任意一点的位置坐标矢量r可表示成形函数矩阵S和单元广义坐标列阵e的表达式:

表1 二维横向高阶ANCF梁单元Table 1 Two-dimensional transverse high-order ANCF beam element

(1)

式中：形函数S是单元坐标x和y的函数，是2×n矩阵函数，n代表单元自由度数。

拉格朗日方程是建立单元运动微分方程的常用方法，其表达式如下:

(2)

式中：QK为广义外力列阵;t是时间。

在利用拉格朗日方程建立单元运动微分方程时需要建立单元的动能T和应变能U微分方程,且有：

(3)

根据公式(3)得单元的质量矩阵为：

(4)

式中ST是形函数矩阵的转置。

超弹性材料单元应变能U是由单元应变能密度函数积分得到。将动能和应变能代入拉格朗日方程，则单元的运动微分方程为：

(5)

式中：QT为单元弹性力列阵，由单元应变能U对单元节点广义坐标e求偏导得到。

2 不可压缩超弹性本构弹性力模型

橡胶材料的应力与应变关系是非线性的，其材料力学特性目前主要由应变能密度函数来表示[23]。通过对应变能密度函数积分得到应变能，应变能对单元广义坐标列阵e求偏导得到弹性力列阵。为了保证单元的不可压缩性，课题组采用了罚函数法。

2.1 Neo-Hookean模型

不可压缩Neo-Hookean模型的应变能密度函数为:

(6)

式中：C=JTJ是右格林柯西应变张量;J是位置梯度矩阵;tr(C)是矩阵C的迹;det (J)是矩阵J的行列式，为了满足单元的不可压缩性，通过不断的调整惩罚系数α，使得det (J)=1;C10是材料系数。

对于初始是直梁的情况，根据方程(1)，单元内任意一点的位置梯度：

(7)

式中：r1x和r1y是r1分别对x和y的导数；r2x和r2y是r2分别对x和y的导数；S1x和S1y是S1分别对x和y的导数；S2x和S2y是S2分别对x和y的导数。将式(7)代入式(6)，并进行积分得不可压缩Neo-Hookean模型的应变能为：

(8)

将方程(8)对单元节点广义坐标列阵e求导，得单元弹性力列阵QT，并根据方程(7)可进一步将单元弹性力列阵表示为：

(9)

2.2 Mooney-Rivlin模型

不可压缩Mooney-Rivlin模型的应变能密度函数为：

(10)

式中C10，C01是材料系数。

将方程(7)代入方程(10)并进行积分，得不可压缩Mooney-Rivlin模型的应变能为：

(11)

将方程(11)对单元节点广义坐标列阵e求导，并根据方程(7)进一步推导出单元弹性力列阵：

(12)

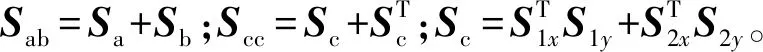
2.3 Yeoh模型

不可压缩Yeoh模型的应变能密度函数为：

(13)

式中C10，C20和C30是材料系数。

将方程(7)代入方程(13)，并进行积分得不可压缩Yeoh模型的应变能为：

(14)

将方程(14)对单元节点广义坐标列阵e求导，并根据方程(7)进一步推导单元弹性力列阵：

(15)

3 算例分析

课题组利用静态和动态大变形实例研究了3种不可压缩超弹性模型Neo-Hookean，Mooney-Rivlin和Yeoh，以及二维绝对节点坐标高阶梁单元模拟橡胶梁大变形力学特性的有效性。

3.1 静态大变形

静态大变形实例选用的是受重力作用的橡胶悬臂梁。静态悬臂梁模型如图1所示，橡胶梁左端固定，另一端自由，整个梁在自身重力作用下产生大变形。重力常数g=9.81 m/s2，橡胶梁长l=160 mm，宽w=7 mm，高h=5 mm。橡胶梁材料参数如表2所示。其中Neo-Hookean模型与Yeoh模型参数与文献[18]中使用参数相同，材料密度为2 150 kg/m3，Mooney-Rivlin模型参数与文献[19]中使用参数相同，材料密度为7 200 kg/m3，选取惩罚系数α=1 000 MPa。

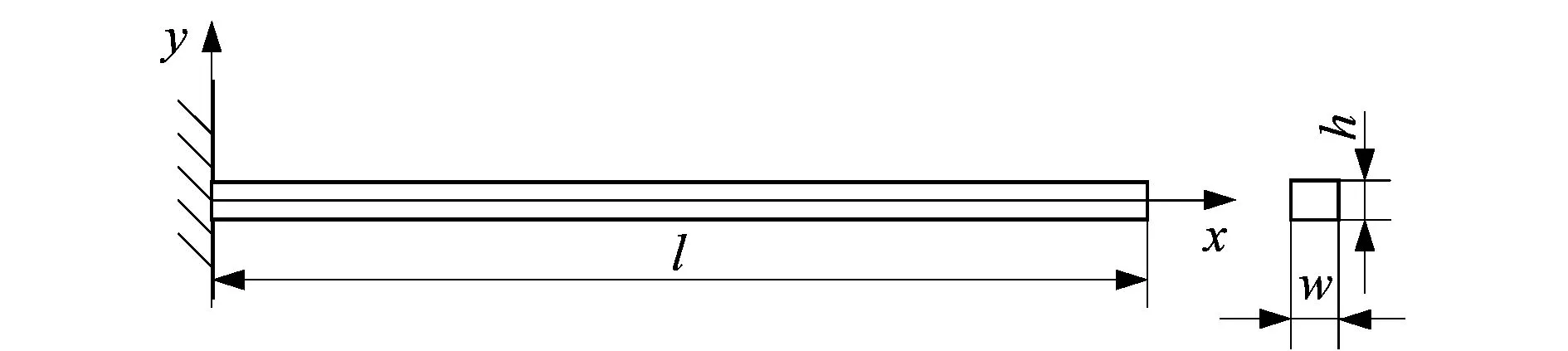
图1 静态悬臂梁模型Figure 1 Static cantilever beam model

表2 各模型的材料参数Table 2 Material parameters of each model

3.1.1 收敛速度

在采用Neo-Hookean，Mooney-Rivlin和Yeoh的3种不可压缩超弹性模型下，HB2n-12，HB3n-12和HB2n-16的收敛情况如图2所示。从图2可以看出，在Neo-Hookean，Mooney-Rivlin和Yeoh的3种不可压缩超弹性模型下，HB3n-12收敛需要的单元数最少，HB2n-12次之，HB2n-16最多。

图2 基于不可压缩超弹性模型的二维高阶梁单元计算悬臂梁位移收敛速度Figure 2 Convergence rates of cantilever beam displacement calculated by two-dimensional high-order beam element based on incompressible hyperelastic model

3.1.2 收敛精度

表3所示为各个单元在不可压缩超弹性模型下的悬臂梁自由端部纵横向位移的收敛值，结果与Omar提出的二维绝对节点坐标低阶单元[4]566进行对比，表中用LB2n-12表示该单元模型，亦与ABAQUS的结果对比。从表3可以看出：①二维绝对节点坐标低阶单元在3种不可压缩超弹性模型下的结果与高阶单元和ABAQUS软件的结果相比偏小很多；②对于Neo-Hookean模型，二维绝对节点坐标高阶单元的结果与ABAQUS软件的结果相差较大；③对于Mooney-Rivlin模型，二维绝对节点坐标高阶单元的结果与ABAQUS软件的结果比较接近；④对于Yeoh模型，二维绝对节点坐标高阶单元的结果与ABAQUS软件的结果非常接近。可见Yeoh模型是最适合超弹性大变形分析的，二维绝对节点坐标高阶梁单元从收敛精度的角度最适合超弹性大变形分析。

表3 3种不可压缩超弹性模型下二维高阶梁单元计算悬臂梁位移精度Table 3 Convergence precision of two dimensional high-order beam elements with three incompressible hyperelastic models

3.2 动态大变形

动态大变形实例选用的是受重力作用的柔性单摆，具体模型如图3所示。单摆的物理参数：长l=350 mm，宽w=7 mm，高h=5 mm。材料参数与静力学相同，具体参数如表2所示。单摆的一端通过销与地面连接。单摆初始位置水平，初速度为零。重力常数g=9.81 m/s2。本算例中的柔性单摆在摆动过程中会产生较大变形。

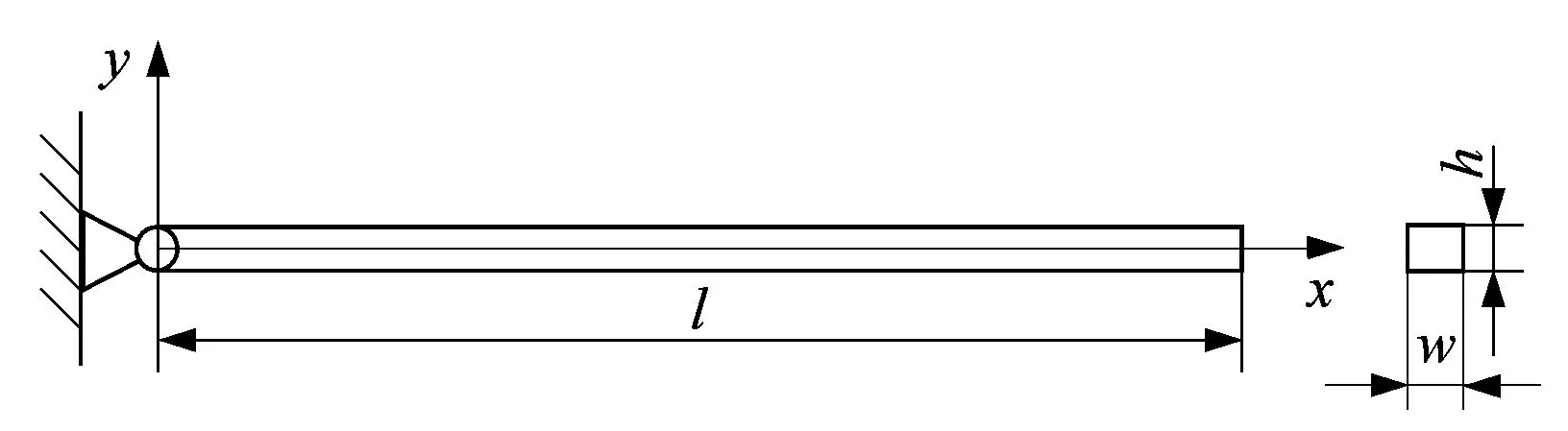
图3 柔性单摆模型Figure 3 Flexible pendulum model

3.2.1 收敛速度

在采用Neo-Hookean，Mooney-Rivlin和Yeoh的3种不可压缩超弹性模型下，HB2n-12，HB3n-12和HB2n-16的收敛情况是基本一致，所以只展示了图4所示的Yeoh不可压缩超弹性模型下，HB2n-12，HB3n-12和HB2n-16的收敛情况。从图4可以看出，HB3n-12收敛需要的单元数是16，而HB2n-12和 HB2n-16收敛需要的单元数是32。

图4 基于Yeoh本构方程不同单元模型的收敛速度Figure 4 Convergence rates of different element models based on Yeoh constitutive equation

3.2.2 收敛精度

根据HB2n-12，HB3n-12和HB2n-16收敛需要的单元数，选择了32个单元分析Neo-Hookean，Mooney-Rivlin和Yeoh的3种不可压缩超弹性模型的计算精度，结果如图5所示。从图5可以看出：①对于Neo-Hookean和Mooney-Rivlin模型，二维绝对节点坐标高阶单元的结果在0.2，0.3，0.4和0.5 s，变形越来越大时与ABAQUS软件的结果相差越来越大；②对于Yeoh模型，二维绝对节点坐标高阶单元的结果在0.0，0.1，0.2，0.3，0.4和0.5 s，与ABAQUS软件的结果都非常接近。因此，Yeoh模型是最适合超弹性大变形分析的。从图5(c)可以看出，二维绝对节点坐标高阶梁单元从收敛精度的角度都适合超弹性大变形分析。

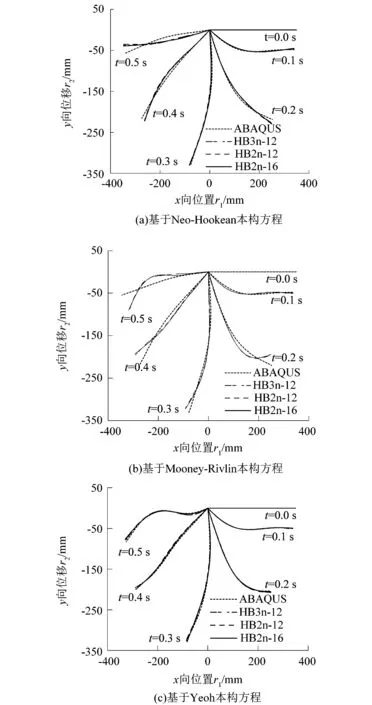
图5 基于3种不可压缩超弹性模型各单元模型模拟的橡胶单摆在不同时刻的构型图Figure 5 Configuration diagrams of rubber pendulum at different moments simulated by each element model based on three incompressible hyperelastic models

3.3 计算效率分析

从3.1和3.2节可知，Yeoh模型是最适合橡胶梁大变形力学特性分析的。橡胶梁大变形力学特性分析需要考虑梁的几何非线性和材料非线性，因此对模型的计算效率提出了比较大的挑战。已知3种二维绝对节点坐标高阶梁单元收敛所需单元数是不同的，HB3n-12收敛所需要单元数最少，最容易收敛，HB2n-12次之，HB2n-16收敛所需要单元数最多。这与单元的构造即单元位移模式和节点广义坐标类型有关。

此外，相同单元数下，3个单元的CPU运行时间也是不一样的。表4所示为HB2n-12，HB3n-12和HB2n-16计算动态大变形实例0.5 s所消耗的CPU运行时间(仿真环境为8 GB运行内存，Inter Core i5-5200U，CPU主频为2.20 GHz的计算平台)。从表4可以看出，在单元数分别是4，8，16和32时，HB3n-12和HB2n-12所消耗CPU运行时间相差不大，HB3n-12比HB2n-12多一些时间，而HB2n-16所消耗CPU运行时间就远多于HB3n-12和HB2n-12，虽然HB2n-16的自由度数16只比HB3n-12和HB2n-12的自由度数12多了4，但CPU运行时间已经达到它们的2倍左右。因此单元自由度数对计算效率影响较大。

表4 各单元CPU运行时间Table 4 CPU running time of each element

4 结论

课题组基于绝对节点坐标法研究了HB2n-12，HB3n-12和HB2n-16的3种二维高阶单元和Neo-Hookean，Mooney-Rivlin和Yeoh的3种不可压缩超弹性模型模拟橡胶梁大变形的力学特性。基于静态和动态大变形实例，分析了3种单元的计算精度和计算效率以及3种不可压缩超弹性模型模拟橡胶梁大变形力学特性的有效性。具体结论如下：

1)Yeoh模型是最适合超弹性大变形分析；从计算精度角度二维绝对节点坐标高阶梁单元都适合超弹性大变形分析，但它们的计算效率相差较大。

2)HB3n-12收敛需要的单元数最少，最容易收敛，HB2n-12次之，HB2n-16收敛所需要单元数最多。这与单元的构造即单元位移模式和节点广义坐标类型有关。

3)相同单元数下，HB2n-16所消耗CPU运行时间是HB3n-12和HB2n-12所消耗的2倍左右，因此单元自由度数对CPU运行时间影响较大。

因此，橡胶梁大变形分析适合采用Yeoh模型，单元多项式位移模式、节点广义坐标类型以及单元自由度数对单元计算效率影响较大。