基于工业机理模型和人工智能算法的零件周期生产量化预测研究

李 贺，吕永松，高雷雷

(中国航发南方工业有限公司，湖南 株洲 412002)

用户短交货期、高质量产品等需求是提高零件制造企业竞争力的重要驱动力。在零件生产过程中，零件的生产周期、生产量等对订单的经济效益有着巨大影响。为提高企业核心竞争力，需要对零件周期生产能力进行有效预测[1-2]。对零件周期生产能力的有效预测既能为企业制定零件周期生产计划提供科学依据，又能对生产资源与生产环节的配置合理性进行正确评估，促使其作用得以充分发挥，从而提升零件周期生产能力。如董海等[3]256使用蜻蜓算法与最小二乘支持向量机的方法完成量化预测，预测精度较高，但进行每一次预测时，需进行大量复杂条件的运算，系统资源消耗较大；宋宣毅等[4]138使用灰狼算法优化的支持向量机完成量化预测，预测资源消耗较小，但针对大量生产数据的预测效果较差。

工业机理模型是依据生产对象、生产过程等构建的精确数学模型，具有很好的模拟效果；卷积神经网络具有表征学习能力，且学习效果十分稳定。因此，课题组提出基于工业机理模型和人工智能算法的零件周期生产量化预测方法，通过对零件周期生产能力的有效预测，提升零件制造企业的经济效益，巩固其在市场竞争中的有利地位。

1 基于工业机理模型和人工智能算法的零件周期生产量化预测

1.1 零件周期生产能力影响因素的工业机理分析

通过对零件生产企业的实际考察和分析，当设备参数固定时，影响零件周期生产能力的因素主要表现在:生产设备维护质量、生产人员的综合素质和生产技术等方面。将这些影响因素作为衡量零件周期生产能力的基础指标，并使用设备作业周期时间、资源单耗以及系统正常运行时间对其进行量化反映，即衡量零件周期生产能力的量化指标，具体影响零件周期生产能力的因素如图1所示。

图1 零件周期生产能力影响因素Figure 1 Influencing factors of parts cycle production capacity

1.1.1 生产设备维护质量

零件生产系统中，各环节设备状态对该系统正常运行具有直接影响。若某一环节设备发生故障，零件生产系统将会停止运行，从而严重耽搁零件生产进程。因此，生产设备维护质量关系着零件周期生产能力；生产设备维护质量越高，其正常运行时间越长，零件周期生产能力就越强[5]。

1.1.2 生产人员的综合素质

生产人员的工作能力、态度和执行力等，在零件生产过程中，极大地影响了零件周期生产能力；综合素质越高，零件生产进程推进越顺利，零件周期生产能力就越强。

1.1.3 零件加工工艺

在设备参数不变的条件下，工艺参数的设置，以及热处理、硫化和切割等加工工艺环节的标准工时均会对零件周期生产能力产生一定程度的影响。若想使设备的作用得以充分发挥，提高其零件产量，应对相关工艺参数进行合理的设置，并严格按照各环节标准工时进行操作。

1.1.4 生产技术

生产技术对零件生产工序以及生产方式作出明确规定;同时零件加工时间、加工精度和人员安排等，也由生产技术进行定义。因此，生产技术对零件周期生产能力起着决定性作用，不断优化生产技术，可促进零件周期生产能力的提高。

1.1.5 零件质量

零件质量通常使用零件合格率进行衡量：如果零件合格率较低，将产生延期交付、重复生产等多余损耗，使得零件周期生产能力严重降低[6-7]；如果零件合格率较高，不仅能提升生产效率，还会使交付周期与生产成本大大缩减，使零件周期生产能力得以充分发挥。

1.1.6 生产环境

生产环境主要体现在零件生产部门分工、生产设备安排及布局上。只有各部门分工明确，合理安排设备布局，才能保证资源的有效利用，以及零件生产进程的顺利推进，提高零件周期生产能力。

1.1.7 生产方式

采取科学、合理的零件生产方式，可最大限度地消除冗余，保证零件周期生产能力的全面发挥。

1.1.8 物料

物料包括零件生产所需的各种物质材料，物料的供应情况、搬运周期等对零件生产具有很大影响，若在零件生产过程中，物料没有及时供应，或者搬运周期长，则会产生停工、生产进程缓慢等问题，使零件周期生产能力大大降低[8]。

1.2 基于卷积神经网络的零件周期生产量化预测方法

零件周期生产量化预测是多元、非线性问题，卷积神经网络具有并行性高、容错性良好和信息处理能力强等优势[9-11]。将其引入零件周期生产量化预测过程中，以获得准确、可靠的预测精度[12-13]。根据文中对工业机理分析，可将零件周期生产量化预测近似为线性关系，将3个量化指标作为卷积神经网络(CNN)的输入，零件周期生产能力作为卷积神经网络的输出，具体操作如图2所示。

图2 卷积神经网络结构Figure 2 Structure of convolution neural network

零件周期生产能力影响因素集合为X，CNN第i层的特征因素为Hi，且H0=X。当Hi为卷积层时的生成步骤：

Hi=f(Hi-1⊗Wi+bi)。

(1)

式中：第i层偏移向量为bi；权值向量为Wi；卷积运算用⊗描述；激励函数为f(x)；Hi可通过对卷积输出及bi进行求和，并使用f(x)获得。

当Hi为下采样层时：

Hi=sunsampling (Hi-1)。

(2)

卷积神经网络在进行多次卷积与下采样的交替操作后，使用全连接层实施分类[14]，则有

Y(i)=P(L=li|H0;(W,b))。

(3)

式中：第i个标签种类为li；概率分布用Y表示。

分析公式(3)可知，通过多层次的数据转换、降维将H0映射到Y上为CNN的本质。

设置L(W,b)描述损失函数，CNN的训练方向为使L(W,b)最小。使用损失函数计算前向传导后的输入H0和期望值WT间的差别，即残差。则有：

(4)

(5)

式中：MSE (W,b)为均方误差函数；NLL (W,b)为负对数似然函数。

引进范数L2和参数λ，对权值过拟合及其强度进行控制，使网络过拟合减少，表示如下：

(6)

通过梯度下降法训练CNN网络各层的W,b参数，能够确保残差在网络中完成反向传播，实现网络不同层的全面更新[15]。学习速率η能够对残差反向传播强度进行控制，表示如下：

(7)

(8)

2 结果分析

以某零件制造企业作为实验对象，验证零件周期生产量化预测的有效性与可行性。

该企业共有10条零件生产线，可生产不同型号的零件产品，详情如表1所示。

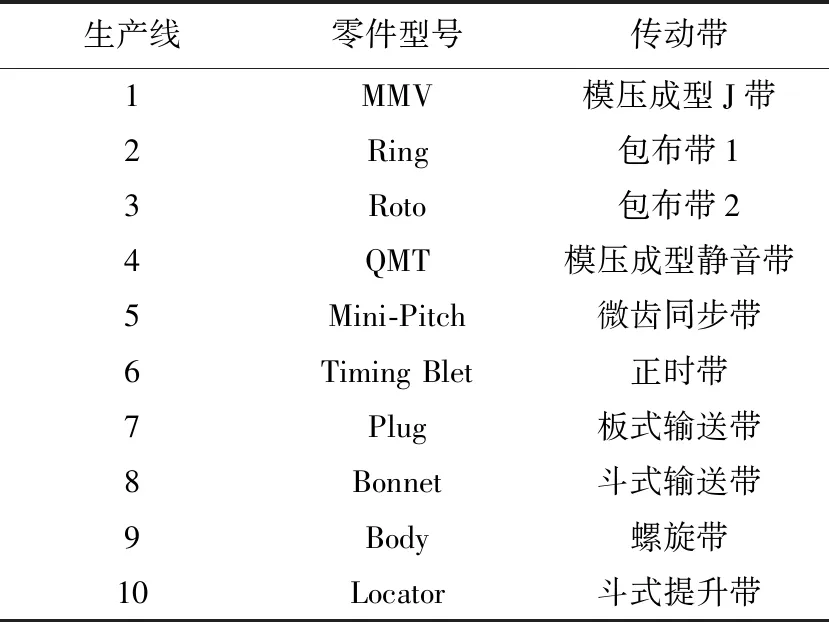
表1 生产线详情Table 1 Details of production line

每条生产线使用不同的零件加工工艺，以生产线2的Ring零件为例，根据加工工艺可生产出4种不同类型的零件，零件加工工艺各环节标准工时如表2所示。

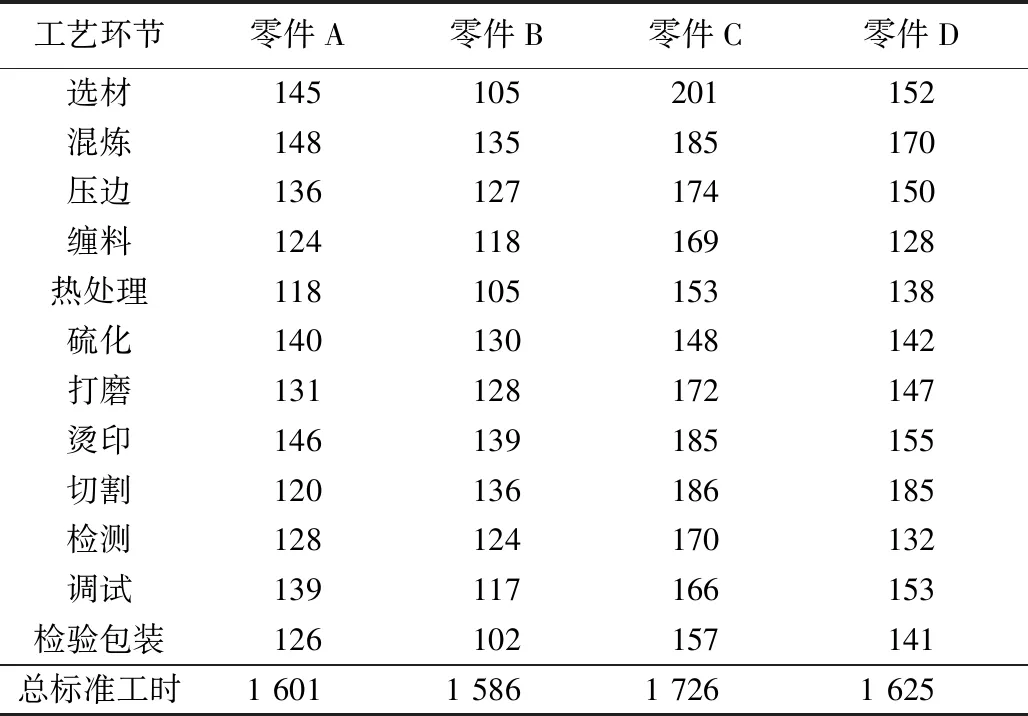
表2 零件加工工艺各环节标准工时Table 2 Standard working hours of each link of parts processing process s

根据零件周期生产能力影响因素的工业机理分析可知，这些影响因素是网络的输入项，将训练真实值与网络输出的预测值进行对比，验证本研究方法的零件周期生产量化预测精度，其中各影响因素用1～8的自然数表示，结果如图3所示。

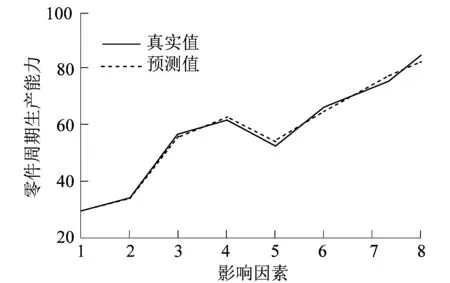
图3 训练结果与预测结果对比Figure 3 Comparison of training results and prediction results

由图3可知，真实值和预测值2条曲线几乎完全重合，表明网络输出的零件周期生产能力预测结果和网络训练获得的真实结果基本一致，误差较小。因此本研究方法具有较高的零件周期生产量化预测精度，可以满足企业生产要求。

设置卷积核大小为3×3，训练次数为200，测试不同学习速率η下，零件周期生产量化预测的命中率以及损失函数变化情况，结果如表3和图4所示。

表3 不同学习速率的预测命中率Table 3 Prediction hit rate results of different learning rates

图4 不同学习速率的损失函数变化情况Figure 4 Variation of loss function at different learning rates

分析表3可知，当学习速率为0.100 0 Mibit/s时，预测命中率最低，仅为58.36%；当学习速率为0.005 0 Mibit/s时，预测命中率高达95.87%。由图4可得，当学习速率为0.100 0 Mibit/s时，随着训练次数增加，其损失函数曲线产生剧烈波动，收敛效果较差；当学习速率为0.005 0 Mibit/s时，损失函数曲线较为平滑，收敛效果较好。综合以上实验结果，将学习速率设置为0.005 0 Mibit/s，不仅能获得较快的收敛速度，还能获得较高的预测命中率，从而使零件周期生产量化预测效果大大提升。

设置学习速率为0.005 0 Mibit/s，测试不同卷积核大小下，零件周期生产量化预测的命中率以及损失函数变化情况，结果分别如表4和图5所示。

表4 不同卷积核大小的预测命中率结果Table 4 Prediction hit rate results of different convolution kernel sizes

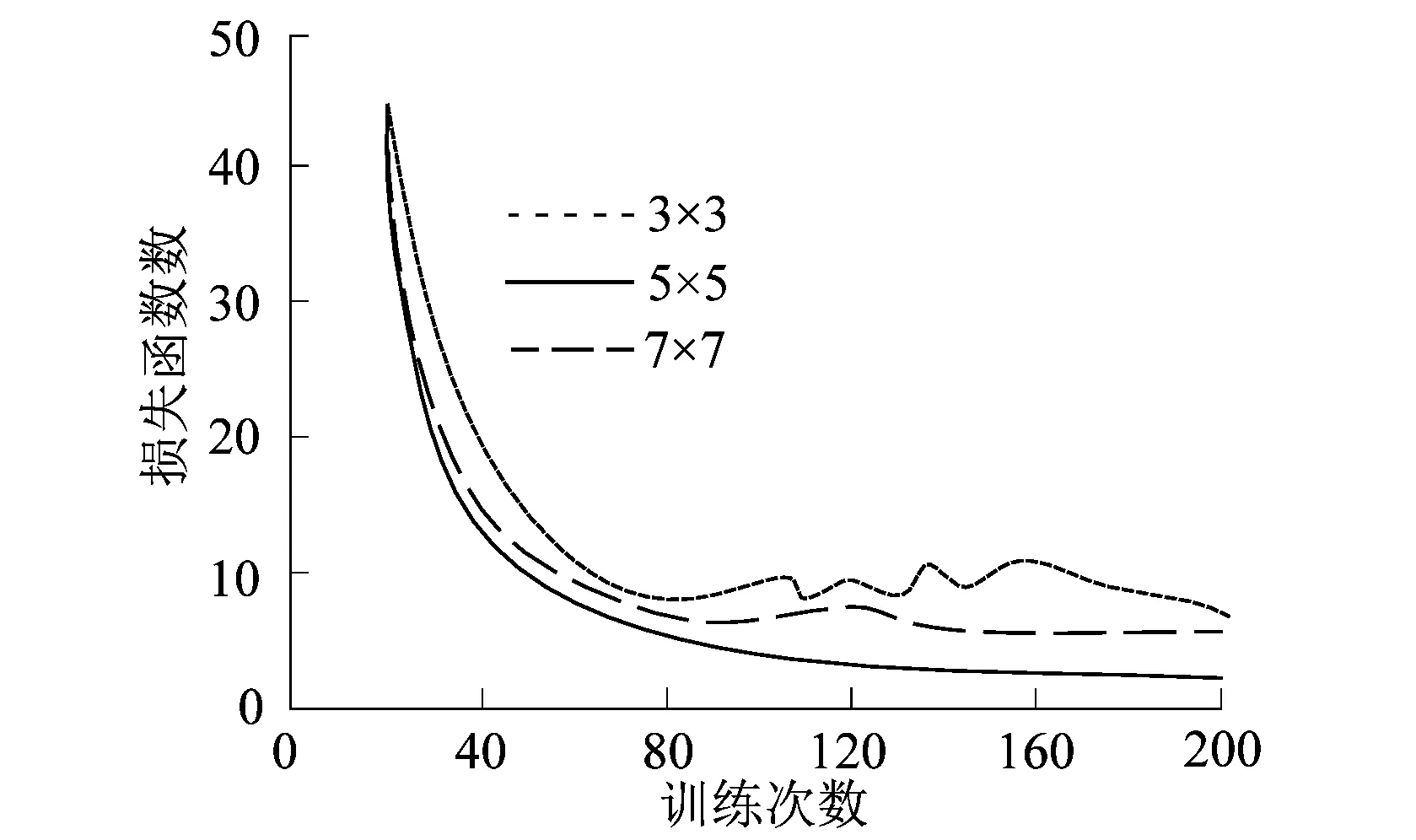
图5 不同卷积核大小的损失函数变化情况Figure 5 Variation of loss function with different convolution kernel sizes

分析表4可得，随着训练次数增加，预测命中率呈上升趋势，3×3卷积核的预测命中率相对较低，最高值仅为85.66%；7×7卷积核的预测命中率相对较高，最高值可达89.31%；5×5卷积核的预测命中率始终高于90.00%，当训练次数增加至500时，预测命中率高达99.73%。由图5可得，5×5卷积核的损失函数曲线能更快地达到收敛。实验结果表明，将卷积核大小设置为5×5，可进一步提升零件周期生产量化预测效果。

以表2中零件加工工艺标准工时作为测试对象，验证零件周期生产量化预测效果，并设计对比实验，选择蜻蜓量化预测方法[3]257与灰狼量化预测方法[4]138作为本研究方法的对比方法，3种方法的零件周期生产量化预测结果如图6所示。

图6 零件周期生产量化预测结果对比Figure 6 Comparison of quantitative prediction results of parts cycle production

由表2可知，加工4种零件的标准工时为零件C>零件D>零件A>零件B，工时越多，零件生产越慢，其周期生产能力就越低。分析图6可得，本研究方法的预测结果与实际结果基本相同，其它2种方法均出现明显误差。因此可以说明，本研究方法具有较高的量化预测准确性，零件周期生产量化预测效果具有优势。

3 结语

信息技术和电子商务的广泛普及，使零件制造企业间的竞争日渐激烈，为了精准预测零件周期生产力，提高零件周期生产能力，课题组进行了零件周期生产能力影响因素的机理分析，结合卷积神经网络，通过多层次的数据转换、降维，将零件周期生产能力映射到激励函数与损失函数上，完成基于工业机理模型和人工智能算法的零件周期生产量化预测方法设计，提高了量化预测精度以及零件生产质量，零件周期生产量化预测效果较好，为制造领域各类生产问题的研究提供参考。

但是本研究尚未对机构的零部件进行受力分析，因此，在未来的研究中，需要针对零件生产过程中的力学性能，建立静力学和动力学平衡方程，为零件供应链的高效运行提供保障。