广义Jacobsthal数及其组合意义

杨胜良, 任凤云

(兰州理工大学 理学院, 甘肃 兰州 730050)

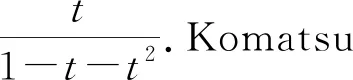
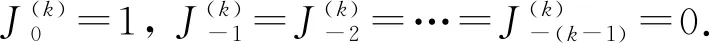
(1)

定理1设J(k)(t)为k-Jacobsthal序列的发生函数,则

(2)

证明由递推关系(1)有

故可得

从而

移项即证.

本文研究了两类格路的计数问题,得到了两个Riordan矩阵,它们的行和或上对角线的和等于k-Jacobsthal数.从而给出了k-Jacobsthal数的组合解释.以下给出本文用到的有关Riordan矩阵的概念.

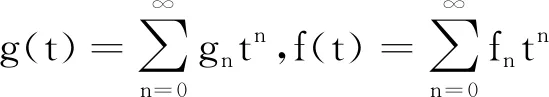
所有的Riordan 矩阵的集合在其乘法法则下构成一个群.Riordan群的乘法法则如下:

(g(t),f(t))(h(t),l(t))=

(g(t)h(f(t)),l(f(t)))

引理1[8-10]设D=(g(t),f(t))是Riordan矩阵,并且V是列向量,v(t)是V的发生函数.则它们的乘积的发生函数为g(t)v(f(t)).

若Riordan矩阵(dn,k)n,k≥0=(g(t),f(t))的第0列定义如下,

n≥0

则

式中

定义3[12]设D是Riordan矩阵,若满足:

则称bk是矩阵M的上对角和.

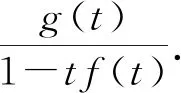
1 k-Jacobsthal数第一个组合解释

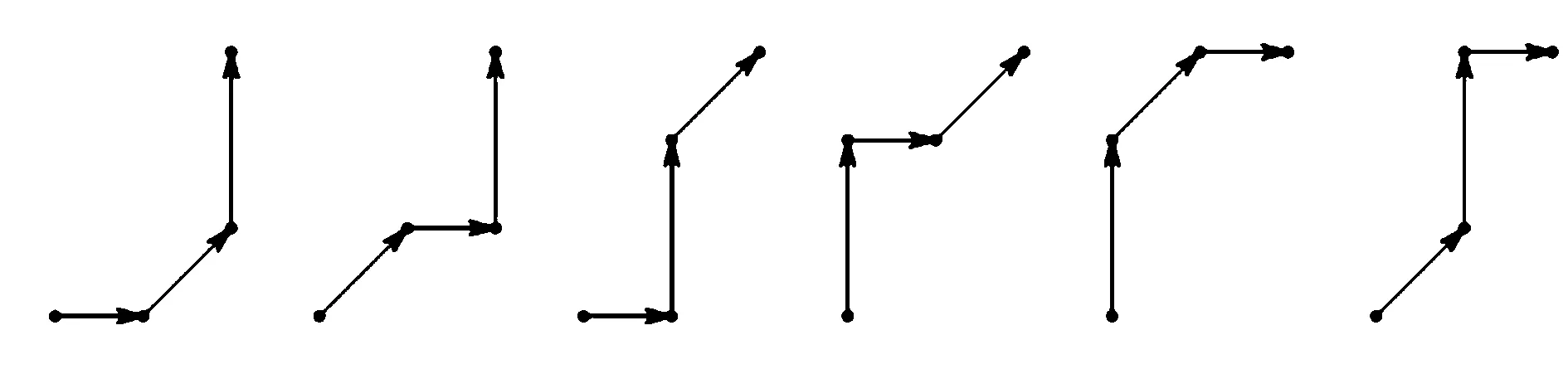
图1 G2(2,3)中的6个格路

由于Gk(n,m)任何格路的最后一步来自于Sk中之一, 故有递推关系式如下形式:

(3)

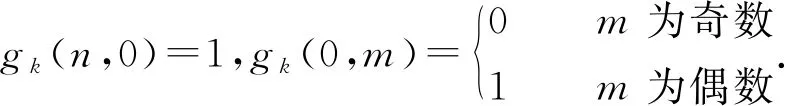
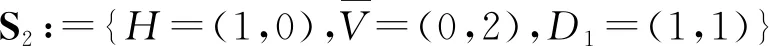
图2 点(n,m)上的数字代表g2(n,m)

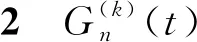
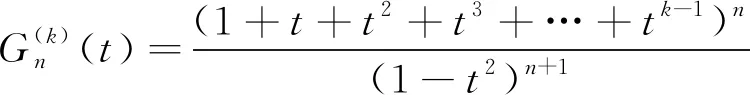
(4)

证明通过递推关系(3)有

从而

因为

递归有

代入即证.

定理3gk(n,m)表示成以下形式:

证明取tm前的系数可得

由卷积公式得

故有

定义5利用gk(n,m)意义下的三角形得

Rk∶=(rk(n,m))n,m≥0如下:

例3当k=2时,R2∶=(r2(n,m))n,m≥0的部分元素如下:

定理4Rk可以表示成以下的Riordan矩阵的形式:

(5)

证明对Rk的(n,m)项取tn前的系数

定理5设Fk(t)为Riordan矩阵Rk的行和的发生函数,则

(6)

证明由引理1 Riordan矩阵与列向量的乘积的发生函数有

化简即证.

对比定理1和定理5可得如下的结果.

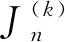
例4当k=2时, Riordan矩阵R2的行和

1,1,3,5,11,21…故Riordan矩阵R2的行和为2-Jacobsthal数,即经典的Jacobsthal数.

定理7k-Jacobsthal 数可以表示为以下形式:

(7)

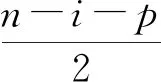
证明因定理3gk(i,n-i)的表达式,故

把gk(i,n-i)代入即证.

利用Riordan矩阵的行和与格路的计数给出k-Jacobsthal数的第一个组合解释.

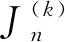
2 k-Jacobsthal数第二个组合解释

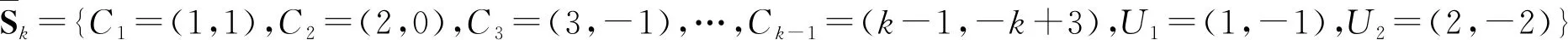
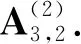
图中的3个格路

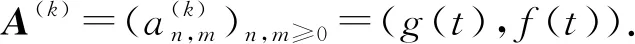
定理9A(k)的Riordan矩阵的形式为

从而

即证.

故有

当k=3时,

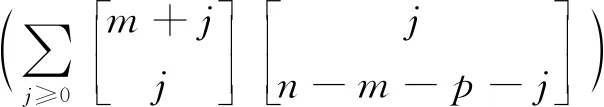
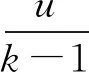
证明取tn前的系数有

由卷积公式有

且

代入卷积公式得证.

定理11设L(k)(t)是Riordan 矩阵A(k)上对角和的发生函数,则

证明由引理3有

化简即得公式.

对比定理1和定理11有如下结果.

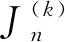
例7当k=2时, Riordan矩阵A(2)的上对角和为1,1,3,5,11,21,….故A(2)上对角和等于经典的Jacobsthal数.

定理12给出了k-Jacobsthal数与Riordan矩阵A(k)上对角和的关系.

故运用Riordan矩阵的上对角和与格路的计数给出k-Jacobsthal 数的第二个组合解释.

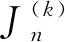
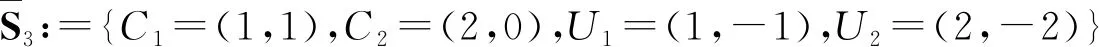
图对j=0,1中的6个格路