有限需求信息条件下鲜活农产品的批发商订货决策研究*

相 征，李煜华，路 璐，向子威

（1.哈尔滨商业大学经济学院，哈尔滨 150028；2.哈尔滨理工大学经济与管理学院，哈尔滨 150080；3.上海应用技术大学经济与管理学院，上海 201418；4.黑龙江大学研究生学院，哈尔滨 150001）

一、引 言

随着生活水平提高，居民对食品及食材的质量要求越来越高。鲜活农产品作为食材的主要来源，其质量越来越受到政府和社会的重视。“十四五”规划和2035年远景目标纲要重点强调“要强化全过程农产品质量安全监管”“加强农产品仓储保鲜和冷链物流设施建设”“广泛开展农产品产销对接活动”。在鲜活农产品市场方面，若要实现供应与需求的有效对接，批发商应采用灵活的订货策略保证鲜活农产品供应，这也是批发商实现自身收益最大化的前提。

国内外有关鲜活农产品订货决策的研究较多，主要集中于构建相应的数学模型探究特定类型的农产品库存与定价策略。早期学者构建的典型库存模型主要包括：Ghare等（1963）建立的以腐败速率为常数的库存模型；Emmett等（2008）建立的易腐产品库存控制模型；Ning等（2013）建立的鲜活农产品库存模型；Qin等（2014）建立的联合定价与库存模型。近年来，国内学者基于早期典型库存模型建立精度更高的数学模型，并开展更深层次研究：王丽娟等（2014）通过构建基于二维Weibull 分布的库存控制模型，分析通货膨胀和延期支付对最优订货量和最小库存成本的影响机制；张伟等（2015）建立供应商一次供货和二次供货模型，得到由一个零售商和一个供应商组成的农产品订货问题解决途径；姚源果等（2019）基于配送路径优化数学模型和蚁群算法，对农产品冷链物流配送的实时路况进行精准信息分析，并得到最优路径；唐振宇等（2019）运用CVaR 模型，发现期权机制可实现供需双方的风险共担；刘墨林等（2020）通过建立分散式、集中式决策模型，对比分析新鲜度需求弹性、服务需求弹性等不同因素对生鲜电商供应链最优决策的影响效应。此外，部分学者探究人的行为和心理对鲜活农产品订货决策的影响。丁松等（2012）探讨随机需求下考虑零售商风险偏好的生鲜农产品最优策略；孙玉玲等（2013）探究损失规避型零售商在库存能力约束条件下的农产品库存决策问题时，通过建立数学模型分析库存约束等对订货量的影响，并证明存在最优解；洪美娜等（2014）构建基于零售商公平关切的鲜活农产品供应链订货决策模型，分析鲜活农产品供应链最优订货策略；聂凯等（2015）从消费者感知视角出发，构造生鲜农产品质量—价格—需求函数和零售商的利润函数，得到零售商一次降价和多次降价情形下最优订货、定价策略；张旭等（2016）通过建立生鲜农产品供应链基准决策模型及数值分析，发现零售商的公平关切会缩短订货周期、降低订货量。随着零售商公平关切度的增大，公平关切效用先增大后减小；税文兵等（2017）采用均值—方差方法建立风险偏好下降的农产品提前采购决策模型，通过算例分析气象灾害和农户故意违约对农户选择和签约量的影响效应；吴春雅等（2019）探究消费者总体及其子群体网购地理标志农产品的意愿与行为偏差，分析个人特征、购买氛围等因素对地理标志农产品消费行为影响的差异性；徐贤浩等（2021）构建二级供应链关于易逝品的最优订货决策模型，发现延迟支付能提高供应链总利润并降低风险；邱若臻等（2021）构建在线零售商两期销售利润模型，发现在线零售商最优定价及库存决策受消费者估值折扣系数和第二期定价策略影响；李琳等（2021）通过研究消费者线上、线下渠道的需求异质性，设计BOPS 服务模式下生鲜品零售定价策略；赵连阁等（2021）建立有调节的中介效应模型，探究劳动力市场分割对农产品流通产业增长的复杂影响机制，找到促进农产品流通产业增长的重要实践路径。

综合上述研究成果发现，鲜活农产品订货决策相关研究经历了从决策者独立且完全理性假设到协调决策的过程，并考虑到行为人心理和风险偏好等因素影响，研究成果对现实更具指导意义。但仍存在以下不足：一是鲜活农产品在供应期内可多次订货，但部分文献并未考虑该因素的影响；二是鲜活农产品在供应期内不同时段的需求不同，往往受各因素影响，应动态预测鲜活农产品需求；三是鲜活农产品的历史需求信息往往有限，需求分布也较难通过分布拟合得到，而大多数文献仍以需求服从某种分布为假设前提。基于此，本文在借鉴现有研究成果的基础上，针对需求信息有限条件下鲜活农产品的批发商订货决策问题进行研究。首先，结合有限需求信息利用组合预测模型对鲜活农产品预测点需求进行预测；其次，对组合预测模型在历史数据点上产生的预测误差进行累计分布，得到有限需求信息条件下预测误差的累计分布，以此作为预测点的误差累计分布，同时以预测点的预测值为均值，可得预测点的需求累计分布；最后，结合随机性存储模型的(s,S)型存储策略得到鲜活农产品批发商订货决策，为鲜活农产品批发商订货决策提供指导。

二、鲜活农产品需求信息分类

鲜活农产品在供应期内，通常需要在冷藏条件下储藏和流通，流通过程中容易发生质量下降情况，故具有库存成本较高、库存时间较短等特点。同时，鲜活农产品的品质往往随保存时间延长而逐渐下降，部分产品表现尤为突出（如海鲜、不易保存的水果等），一旦质量下降，批发商利润率就会下降，甚至发生亏损，故批发商在经营过程中会更加重视鲜活农产品需求信息。

鲜活农产品需求信息是指所有能够反映鲜活农产品需求规律的内容。从需求预测角度分析，鲜活农产品需求信息包括反映鲜活农产品需求变动和需求预测效果两部分信息。鲜活农产品需求变动包括不同时段需求的变动和同一时段需求的波动。据此，本文将反映鲜活农产品需求变动的信息分为稳定性信息和不稳定性信息，前者主要包括季节、节假日和价格（价格政策）等，而后者主要受到气温和市场供求关系（表现在价格波动）等因素影响，两者均可通过引入相应变量进行处理。此外，稳定性需求信息还应包括鲜活农产品的历史销售数据，因为历史销售数据是各种影响因素综合作用的结果，集中反映了鲜活农产品需求变动结果，最能反映鲜活农产品过去的需求趋势。鲜活农产品需求变动信息常用来建立需求预测模型，以预测鲜活农产品供应期内需求。

反映需求预测效果的信息主要用于鲜活农产品需求预测的误差上。预测误差难以避免，通过合适的方法对预测误差补偿，是降低预测误差影响的主要途径。研究者希望通过建立需求预测模型充分利用反映产品需求信息，减小预测误差，却忽视了预测误差也是产品需求预测信息的重要组成部分。误差补偿在发现误差规律的基础上，应用误差规律弥补在预测过程中遗失掉的信息，从而提高预测精度。有关误差补偿的研究和应用较多的领域集中于利润或价值相对较高的行业，如股票价格预测、精密工业制造等领域（Mahmud等，2015；沈传茂，2014；Tatar 等，2012；Huo等，2012）。虽然鲜活农产品需求预测的误差分布未知、误差数据又相对有限、误差出现的概率也不确定，但挖掘和利用鲜活农产品需求预测的误差信息却是鲜活农产品批发商提高需求预测精度，进行科学订货决策的途径之一。

三、组合预测及随机性存储模型

（一）组合预测

组合预测指使用两种或两种以上的预测方法建立预测模型进行预测，在产品需求预测方面的预测精度比现有其他预测方法要高（倪冬梅等，2013）。常见的组合预测模型包括自回归移动平均整合ARI⁃MA（autoregressive integrated moving average）模型与多元回归的组合模型和支持向量机回归SVR（sup⁃port vector regression）与ARIMA 的组合预测模型等。相比于单一预测，组合预测可充分利用不同预测方法的优势使预测结果相对更准确。在产品需求预测方面，应用较多的是时间序列与多元回归的组合预测模型。具体思想首先是利用时间序列分析工具（如Eviews）对历史数据进行建模，得到模型的有关参数和第t期的预测值其次将与其他影响因素放在一起建立多元回归模型，最后利用该组合预测模型预测产品需求。需要说明的是，如果值过大，可修正处理后再建立预测模型。

（二）随机性存储模型

随机性存储模型指需求或备货时间随机，但概率或分布已知（侯宇航等，2015）。从批发商角度看，鲜活农产品的需求明显是随机、连续的，且受到多种因素影响，但供应期内鲜活农产品的供货及备货时间均相对稳定。

需求是连续变量的随机性存储模型假设如下：产品成本为K，单位售价为P，单位存储费用为C1，单位缺货费为C2，每次的订购费为C3，需求r是连续随机变量，其密度函数为分布函数期初存储为I，订货量为Q，期初库存为S=I+Q。则本阶段订货费为C3+KQ，存储费期望值为缺货费的期望值为则总费用的期望值为上述三者之和，并记为C(S)，C(S)是S 的连续函数。令dC(S)/dS=0，经计算化简得则订货量为Q=S-I。若不发生订货，当存储为s，如果此时费用的期望值与发生订货的期望值相等，即C(s)=C(S)，则s为订货点，对应的存储策略为(s,S)。另外，需要注意的是，由F(S)的关系式可看出，期初库存S与需求的累计分布有关，在不确定需求服从何种分布时，若能计算出需求的累计分布就可得到期初库存量，进而确定订货量。

四、鲜活农产品预测点的需求累计分布与订货决策

（一）估计预测点的需求累计分布

鲜活农产品的需求在供应期内不同时间段不一样，在不同年份的同一时间段也有差异。因此，对鲜活农产品批发商而言，通过鲜活农产品的历史销售数据进行分布拟合得到需求预测值并不能很好地反映鲜活农产品的现实需求。本文在分析鲜活农产品需求预测误差特征的基础上，结合误差补偿得到鲜活农产品预测点的需求累计分布的估计。

鲜活农产品的需求预测误差具有两个特征：一是有界，鲜活农产品需求有界，故其误差必定有界；二是分布未知，鲜活农产品需求信息有限导致需求预测误差数据有限，这也是鲜活农产品需求预测误差分布未知的原因。

虽然鲜活农产品需求预测误差的分布未知，但预测误差的累计分布却已知，可通过预测误差数据的统计处理得到。需求预测误差的累计分布表示小于某一数值的预测误差出现的概率，预测误差越大，预测值出现的概率则越小。

预测点的需求预测误差是总体需求预测误差的一部分，同样具有上述性质。基于预测点需求预测误差性质和随机性存储模型中订货量特征，本文采用历史销售数据预测误差的累计分布代替预测点需求预测误差的累计分布，得到鲜活农产品在预测点的需求累计分布的估计，具体步骤如下。

第一步：确定鲜活农产品需求的影响因素，通常有价格、季节、节假日和气温等，必要时需归一化处理。

第二步：用组合预测方法对预测点进行需求估计。首先，分析历史需求数据（可用历史销售数据代替）之间关系，得到预测点与前期历史数据的表达式；其次，建立包含鲜活农产品需求的影响因素和历史需求数据的组合预测模型；最后，用该组合预测模型对预测点预测，得到预测点的估计值

第三步：估计预测点的需求累计分布。根据鲜活农产品组合预测模型的各个历史销售数据点的估计值，得到历史销售数据点的预测误差对σ进行处理，得到σ的累计分布，以此代替预测点的需求预测误差ε的累计分布。最后，以预测点的估计值作为该点的均值结合预测误差ε的累计分布，得到预测点Df的累计分布。因为由统计学相关知识可知，Df的累计分布实质由ε决定。

（二）鲜活农产品订货决策分析

鲜活农产品随机性存储模型较一般的随机性存储模型，具有如下特点：

（1）产品的成本会随着供求关系变化。鲜活农产品生长周期长，一旦产品供应不足，短时间内供求关系不能改变时，必然会影响批发商采购成本。

（2）单位存储费用会随季节有较明显变动。鲜活农产品在冷藏条件下流通和储藏，会受到外界温度影响，夏季温度较高，制冷所需费用就较高，故单位存储费在不同季节会有较大变动。

（3）需求易受到价格影响。鲜活农产品并非必需品，故需求弹性相对较大，这也是鲜活农产品常通过降价达到促销目的的原因。

（4）订货点可视为零。鲜活农产品的价值在经过一段时间销售后，产品质量会下降，若将其与新到货的鲜活农产品一起售卖，很可能失去销售机会。故通常情况下，鲜活农产品批发商会在下次到货前，通过降价等促销方式消化库存。

基于以上考虑，假设期初库存为0，将Df带入随机性存储模型，经计算化简为式（1）。

由式（1）可知，订货量受单位存储费用C1、单位缺货费C2、产品成本K 的共同影响。订货量随单位存储费用C1的增加而减少，随单位缺货费C2的增加而增加。

由式（2）可知，订货量随产品成本K 的增加而减少。另外，订货量受预测点需求累计分布的影响，即受鲜活农产品需求预测误差ε的影响。

（三）鲜活农产品订货决策过程

鲜活农产品订货决策过程如图1所示。在得到鲜活农产品需求信息后，需先计算出预测值并推算σ、ε等相关参数的累计分布，再带入随机型存储模型做出相应决策。

五、实例应用

本文以上海某农贸市场雨润公司冷鲜猪肉销售为例，分析该市场批发商的订货决策。冷鲜肉销售记录选自2019年3月5日到10月7日，根据雨润公司2020年年度报告，雨润公司生产冷鲜肉的成本为K=19，每单位批发价格为P=25。农贸市场中冷鲜肉单位存储费用C1=2，单位缺货费C2=25，每次订购费C3=200，通常情况下冷鲜猪肉的保质期为一周，冷鲜肉零售价格随行就市。

（一）冷鲜猪肉需求信息处理

对公司调研后，选取以下信息作为该公司产品需求信息做相应处理：季节变量用Si（i=1,2,3,4）分别表示春、夏、秋、冬，Si取值为0或1，取任意两个值为1。取一天的最高气温与最低气温的平均值作为该日气温，将一周内七日气温平均值作为该周气温值，记为Tt（t=1,2,…,31）。将一周内该公司冷鲜肉价格平均值作为该周价格，记为Pt（t=1,2,…,31）。将节假日按照假期的天数分为两类，清明、劳动节、端午和中秋节等有三天假期的节假日归为一类，国庆节等有七天假期的节假日归为另一类，用Hit（i=1,2；t=1,2,…,31）表示，Hit取值为0或1。销售量受价格影响明显，故取每周降价前的历史销售数据之和作为每周需求数据，记为Dt。最后，对气温、价格等做归一化处理。

（二）估计预测点需求累计分布

利用Eviews7.2对历史销售数据做时间序列分析，得到历史销售数据序列间关系如下。

由式（3）可见，第t期需求量与第t-1期、第t-2期有关，同时受到移动平均MA(9)项影响，将这三项一起纳入回归模型，得到该公司冷鲜猪肉需求预测的组合预测模型如下。

该需求组合预测模型的系数检测和整体预测效果检验结果如表1、表2所示。

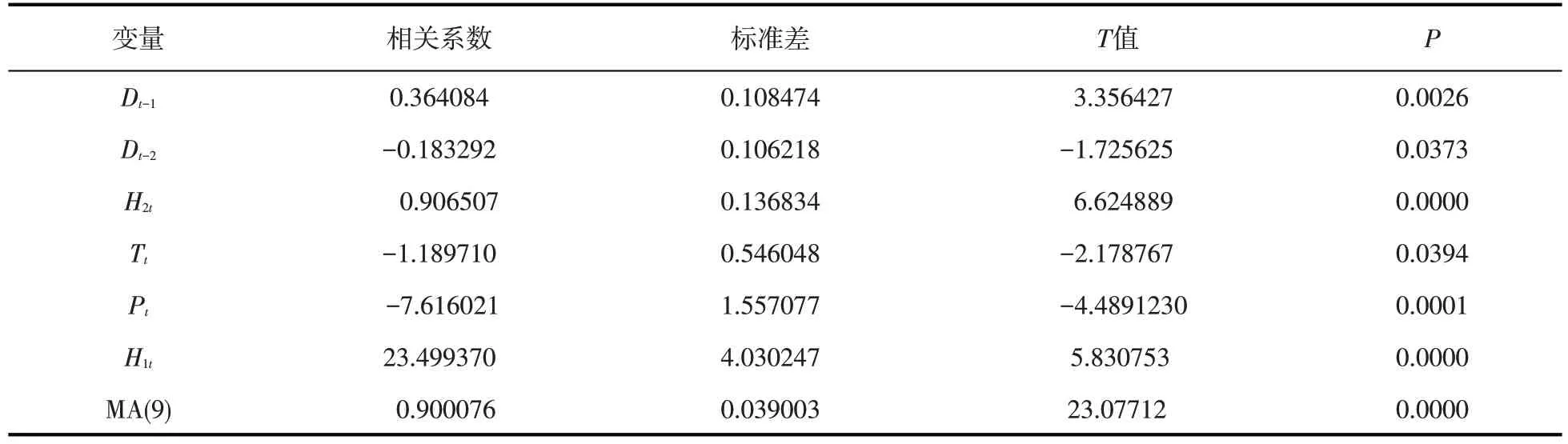
表1 组合模型的系数检验表

表2 组合模型的整体效果检验表

由表1、2可知，各变量均通过5%水平的显著性检验且相关系数数值合理（见表1），组合模型的整体效果较好，变量相关系数数值合理，R值为0.89近似为0.9，调整后R值为0.87大于0.85，AIC值和SC值合适且充分小，同时一阶残差几乎不相关（DW 值近似为2），说明组合模型合适（见表2）。此外，从组合模型的残差参数检验结果得出（见图2），残差间相关系数的p值均大于0.05，残差间几乎不相关。

利用matlab2012b，对历史销售数据的预测误差σ做累计分布，如图3所示。在计算出σ累计分布的同时观测到σ的累计分布近似服从正态累计分布。

以σ误差累计分布代替预测点预测误差ε的累计分布，以作为均值得到该公司预测点产品需求Df的累计分布。

（三）订货决策结果及对比分析

由组合预测模型得到下一期预测值为9.32个单位，带入随机性存储模型，结合Df的累计分布，可得该期订货量S=8.48个单位。其中9.32单位是结合历史销售数据，使用组合预测方法得出的预测值，也就是预测市场需求量；8.48单位是通过随机性存储模型计算出的订货量。

结合时间序列数据并依靠随机性存储模型计算出订货数量后，采取对比分析的方法证明随机性存储模型的科学性。本文预测订货量为8.50个单位，但样本市场下一时期实际进货量为10个单位，实际销售量为9.1个单位，单纯依靠经验计算进货量导致样本市场产生产品积累并面临着鲜活农产品变质的风险。因此，本文构建的有限需求下鲜活农产品的批发商订货决策体系有一定的实际作用，可以辅助批发商计算进货量，获得更高利益并减少鲜活农产品变质风险。

六、结 论

鲜活农产品具有较强的季节性，不易保管、不耐久藏，且消费需求多变、市场不确定性大，造成批发商订货决策相对困难，本文提出的鲜活农产品订货决策方法具有如下特点。

（1）较为充分地利用了鲜活农产品的需求信息和需求预测误差信息。鲜活农产品订货点的需求信息相对有限，在梳理鲜活农产品需求信息后，建立了鲜活农产品的组合预测模型对鲜活农产品需求进行预测，使得鲜活农产品需求预测相对更加准确。此外，针对组合模型需求预测的误差，利用历史销售数据的误差做累计分布取代预测点需求预测的误差累计分布，从而得到预测点的需求累计分布，避免在销售数据有限条件下直接进行分布拟合所带来的信息流失，为鲜活农产品在有限需求信息条件下充分利用信息和订货决策提供一种新思路。

（2）鲜活农产品的库存决策更具可操作性。鲜活农产品需求预测的组合模型可随需求信息的变更得到相应订货决策模型，可充分利用与近期有关的鲜活农产品需求信息。当新品种的鲜活农产品进入市场时，因缺乏销售记录，本文提出的有关方法可为订货决策提供参考；批发商也可随销售数据的更新及时采取新决策。此外，随着市场价格波动，在利用组合预测模型确定鲜活农产品需求预测的同时，批发商可根据订货的决策模型快速确定鲜活农产品订货量，更具可操作性。