基于ARMA-AO-GARCH的组合预测模型

张艳辉，殷向宇，闫 亮

(河北经贸大学数学与统计学学院，河北 石家庄 050061)

一、引言

随着经济发展和社会进步，人们的投资意识开始转变，越来越多的人开始关注金融投资市场。如何对金融投资市场进行分析和预测，进而帮助投资者进行决策是当前的热点问题。

目前许多学者对金融投资市场进行了预测研究。一些学者使用单一模型进行预测。Harsha等[1]通过构建ARMA模型对股票价格进行了预测。王雨晨[2]对上证指数收盘价构建了ARIMA模型并进行预测。徐珺[3]对黄金期货价格进行平稳化处理，然后对其建立ARMA模型并进行预测。徐泾[4]对沪深300指数收益率进行研究，结果表明GARCH族模型可有效拟合证券投资市场波动特征。由于组合模型能同时兼顾数据线性和非线性特征，更多学者将ARMA模型与GARCH模型结合对金融数据进行预测。Yaziz等[5]通过建立ARIMA-TGARCH模型对黄金价格进行了预测。杨琦和曹显兵[6]通过构建ARMA-GARCH模型对大众公用股票价格进行了分析和预测。王莉[7]基于深圳综指拟合了ARMAGARCH和ARMA-EGARCH两种模型，发现前者更优。潘雪艳[8]对黄金价格建立了ARIMA-GARCH模型并进行预测，取得了较精确的预测结果。

由于金融市场存在个别突出数据会对模型拟合产生影响，所以要考虑到异常值的存在。陈立等[9]在分析黄金定价数据时进行了异常值的检测。但是，经了解，尚未有学者把异常值加入ARMA-GARCH模型之中。因此，为进一步提高对金融数据的预测精度，本文除了考虑到ARMA模型和GARCH模型分别处理线性和非线性数据的优越性外，还考虑到异常值对模型的影响，将可加异常值以外生变量的形式加入ARMA-GARCH模型之中，以提高模型的预测精度。

二、理论模型

(一)ARMA模型

ARMA(p，q)模型，即自回归移动平均模型，是由美国统计学家Box和英国统计学家Jenkins提出的一种时间序列模型。它的一般形式可表示为:

式中:{εt}是白噪声序列，p和q均为非负整数。

(二)可加异常值

异常值是指一些不规则的观测值，其出现可能源自测量误差和复制误差，也可能是源于基础过程发生了突发的短期性变化。异常值可分为可加异常值(AO)和新息异常值(IO)，本文主要介绍可加异常值。AO指的是基础过程在时刻T时受到了可叠加性扰动。如果序列Yt在T时刻出现AO，那么序列就变为了其中为一个脉冲函数，可表示为因此，Y′t还可表示为:

(三)GARCH模型

Engle在1982年首先提出了对金融数据中条件异方差进行处理的自回归条件异方差(ARCH)模型，但当参数过多时，ARCH模型往往不太适用。为解决此缺陷，Bollerslev在1986年提出了广义自回归条件异方差(GARCH)模型，该模型定义如下:

式中，f(t，Yt-1，Yt-2，…)为序列{Yt}的自回归模型；为残差序列；为残差序列在t时刻的方差，反映了序列的条件异方差性。

(四)ARMA-AO-GARCH组合模型

金融数据受到多方面复杂因素的影响，往往具有极强的不确定性，通常表现出明显的波动聚集现象。这时，如果仅用研究平稳序列的ARMA模型来进行拟合，往往不恰当，而ARMA-GARCH模型同时考虑了误差项的同方差和异方差分布。此外，本文还考虑金融数据受到突发事件的影响往往会产生异常值，而其也会影响模型的拟合效果，因此将AO纳入ARMA-GARCH模型之中，建立了ARMA-AO-GARCH组合模型对金融收益率序列进行预测，具体建模步骤如图1所示。

图1 ARMA-AO-GARCH组合模型建模流程图

本文采用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)三项统计学误差指标来评判ARMA-AO-GARCH模型的预测效果，各误差指标越小，模型预测效果越佳，具体表达式如下:

三、实证分析

本文共选取两个金融投资数据集进行实证分析，分别为上证指数收益率序列和黄金价格收益率序列。本文利用R软件进行数据分析及模型建立与预测。

(一)实例一:上证指数收益率

1.数据来源及说明

实例一选取了上证指数的相关数据进行实证研究。选取从2016年1月4日~2021年3月31日共1322个日收盘价格作为样本，数据来源于网易财经网站。由于收益率序列比价格序列具有更好的统计特征，对收盘价格序列计算收益率序列。定义Pt为第t个交易日的收盘价，则收益率rt为:rt＝(Pt-Pt-1)/Pt-1，得到1321个收益率序列，将前1261个数据作为训练集建立模型并进行为期60天的预测，将后60个数据划分为测试集来检验预测效果。

2.描述性分析

为了更清楚地了解上证指数收益率的变化趋势，对其进行描述性分析。

由表1可知收益率序列的均值很小，大于0且几乎为0，表明股票市场的投资回报率较低。偏度为-0.943164＜0，故其为左偏分布。峰度为6.960956＞3，说明其具有尖峰厚尾的特征，且左尾较厚。JB检验p值为0.000000，显著地拒绝了该序列为正态分布的原假设。因此，在后续建模时可以优先考虑更适用的学生t分布或GED分布。

表1 上证指数收益率的统计描述表

3.ARMA模型建立

首先对收益率序列进行ADF单位根检验，结果表明序列是平稳的。然后进行纯随机检验(Box-Ljung test)，结果表明该序列具有自相关性，判断该序列为平稳非白噪声序列，可用ARMA模型拟合该序列。下面使用AUTO.ARIMA函数自动识别模型，该函数可根据AIC准则自动定阶。经识别，模型为ARMA(4，3)模型。

4.异常值识别

使用detectAO和detectIO函数识别ARMA模型中的异常值，经检测，该序列存在7个AO。出现AO的日期分别为:2016年的1月7日、1月11日、1月26日，2018年的10月8日，2019年的2月25日，2020年的2月3日、7月16日。通过查阅资料找到了可能导致出现AO的原因:2016年1月4日起A股开始实行熔断机制，在该机制的保护下，A股市场在1月份开始了下跌浪潮，1月7日与11日均因触发熔断机制使得上证指数下跌。2016年1月26日上证指数下跌了6.42%，产生暴跌的原因有:人民币在该日附近遭遇大幅波动；央行近期频繁释放流动性，因此市场在春节前将转降息或将大概率落空。2018年10月8日是国庆假期后的首个交易日，A股市场受外围市场节日期间大跌影响呈大幅低开，上证指数跌了3.72%。2019年2月21日~24日，中美双方就技术转让、知识产权保护、非关税壁垒等方面的问题进行磋商并取得实质性进展，2月25日，受利好消息刺激，上证指数暴涨5.59%。2020年2月3日，受新冠肺炎疫情影响，上证指数跌了7.72%。蓬佩奥在2020年7月15日晚宣布，美国将对华为部分员工实施制裁，并将对华为等科技公司实施新的签证限制，7月16日上证指数下跌4.5%。将AO纳入ARIMAX模型之中，ARIMAX模型较ARMA的AIC更小，说明加入AO使模型的拟合效果更好。

5.ARMA-AO-GARCH组合模型的建立

对ARIMAX模型的残差使用ARCH-LM法检验是否存在异方差，结果表明存在ARCH效应，也即存在异方差，应建立GARCH模型。在实际应用中，常用的GARCH模型有GARCH(1，1)，GARCH(1，2)，GARCH(2，1)。将上述模型与ARMA(4，3)模型结合并且分别采用t分布、GED分布拟合模型，综合AIC、SC、HQC以及参数的显著性确定最优模型。经过比较，最终模型为ARMA(4，3)-GARCH(2，1)模型，分布为t分布。接下来将AO加入ARMA(4，3)-GARCH(2，1)模型之中，具体操作为:生成一个长度与训练集长度相等的向量作为外生变量，由于AO只在T时刻对序列造成扰动，因此在存在AO的位置设置为1，其余位置均为0。利用external.regressors函数将变量加入ARMA-GARCH模型的均值方程之中，至此建立了ARMA(4，3)-AO-GARCH(2，1)模型。对残差进行ARCH-LM检验，结果表明模型中不存在ARCH效应。

6.模型预测及结果比较

接下来用本文最终建立的模型进行为期60天的预测，此外，对于文中建立的ARMA(4，3)和ARMA(4，3)-GARCH(2，1)模型也均进行为期60天的预测。各模型的预测精度如表2所示。

表2 上证指数收益率不同模型预测精度比较表

由表2可以看出，ARMA模型的预测精度最低，可见单纯地用ARMA线性模型不能充分地提取数据中的信息。对比ARMA-GARCH模型和ARMA-AO-GARCH组合模型，可以看出二者的RMSE相同，而后者的MAE和MAPE均小于前者。总体而言，ARMA-AO-GARCH模型的预测效果最好。

(二)实例二:黄金价格收益率

实例二选取2018年1月1日~2021年3月31日伦敦黄金交易市场下午定盘价格，共847个数据，数据来源于世界黄金协会官网。根据收益率计算公式，计算得到846个收益率序列，将前796个数据划分为训练集，后50个数据作为测试集。

首先对黄金价格收益率进行描述性分析，结果表明该序列与上证指数收益率序列类似，具有明显的波动聚集现象。接下来进行ARMA建模，经识别该模型为ARMA(4，2)模型。然后识别该模型中的异常值，发现存在2个可加异常值。将异常值纳入模型之中，对残差序列进行ARCH效应的检验，发现序列存在明显的ARCH效应。经过识别与比较，最终建立了ARMA(4，2)-AO-GARCH(1，1)组合模型，利用该模型对该序列进行为期50天的预测。同样，建立ARMA(4，2)模型与ARMA(4，2)-GARCH(1，1)进行预测效果的比较，结果见表3。

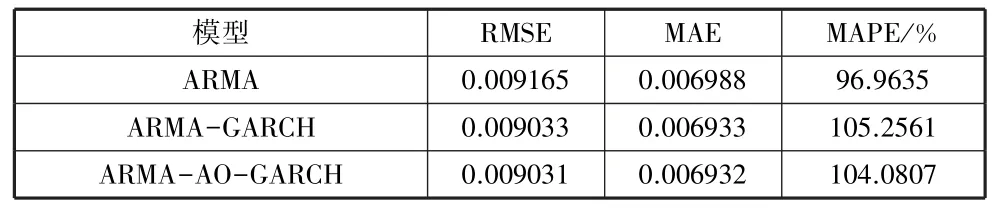
表3 黄金价格收益率不同模型预测精度比较表

由表3可以看出ARMA-GARCH模型与ARMA-AOGARCH模型的MAPE大于ARMA模型，但RMSE与MAE均小于ARMA模型。此外，ARMA-AO-GARCH模型的三项误差指标均小于ARMA-GARCH模型。整体而言，对于该序列，ARMA-AO-GARCH模型的预测效果是最好的。

四、结论

本文充分考虑到金融投资市场的波动聚集性以及易受到异常事件影响的特点，建立了ARMA-AO-GARCH组合模型并将其应用到上证指数收益率和黄金价格收益率的预测之中。此外，本文还建立了ARMA模型和ARMA-GARCH模型与其进行预测精度的对比。实证结果表明ARMA-AOGARCH模型具有较高的预测精度，预测效果总体优于其他两种模型，说明该模型能够很好地拟合和预测股票收益率以及黄金价格收益率等金融投资收益率序列，能够对金融市场的投资、分析以及决策提供一定的参考价值。