车辆跟驰的随机优化速度模型及其稳定性分析

刘中华，舒思朝，吴子强，吴新烨

（厦门大学，建筑与土木工程学院，福建厦门 361005）

0 引言

为揭示车流引发拥堵的内在机理，国内外学者建立了各类交通流模型，其中，车辆跟驰模型对研究交通流特性和调控车流稳定有着重要意义，引起众多学者的关注。车辆跟驰理论是运用动力学方法，在单一车道上假定车辆无法超车且车头间距在一定范围内，此时，后车跟随前车行驶，车辆间产生相互作用并以运动方程描述这种相互作用。CHANDLER 等[1]基于刺激-反应理论在20 世纪中叶提出GM 模型，GM 模型经过众多学者的深入研究，推动了微观交通流理论的发展。此后，跟驰理论不断丰富，BANDO 等[2]提出著名的优化速度模型(OV)，受到广泛的关注和应用。HELBING 等[3]在发现前、后车负速度差的作用后，提出改进的广义力模型(GF)。之后，JIANG等[4]在GF模型的基础上同时考虑正、负速度差均产生影响，提出全速度差模型(FVD)。此后，许多学者在车辆跟驰模型上作出了重要贡献。

以上模型均用确定性函数描述交通流特性，真实的交通流中存在着不可忽视的随机现象，跟驰行为的随机性客观存在。王祺等[5]考虑交通流中的随机性，发现了局部密度-速度的随机分布特性。张建波等[6]提取快速路的车辆跟驰轨迹，得到车头时距的随机特征后，建立了随机Newell 跟驰模型。ZHENG等[7]考虑驾驶员驾驶行为的随机因素，建立随机拉格朗日交通动力学模型。WAGNER 等[8]通过分析车辆轨迹数据后，发现许多跟驰车流产生波动的原因来自于驾驶员自身的随机性。张继业等[9]对交通流随机行为进行分析，认为交通流随机行为对实际交通控制有重要意义。

因此，考虑车流的随机现象会使跟驰模型更加符合现实车流的性质，本文基于优化速度模型将驾驶员的灵敏度系数设定为相同的常数值，没有考虑跟驰过程中驾驶员的灵敏度系数会产生随机变化，将灵敏度系数模型化为高斯白噪声过程，建立随机优化速度模型(SOV)，并进行随机稳定性分析和蒙特卡洛数值模拟，研究结果证实了灵敏度系数的噪声强度对车流扰动传播的影响。

1 随机优化模型建立

1.1 优化速度模型

BANDO 等[2]引入有拐点的优化速度函数，以加速度为研究项建立交通动力学方程，提出优化速度模型，其系统动力学方程为

式中：a为驾驶员灵敏度常值系数；n为第n辆车，n=1,2,…,N，N为系统的车辆总数；t为时间；分别为第n辆车在时刻t的位置、速度、加速度；Δxn(t)=xn+1(t)-xn(t)为跟驰车辆n与第n+1 辆车在时刻t的车头间距；V(·)为优化速度函数，本文优化速度函数表达式为

式中：hc为安全车头间距，本文设hc=25 m ，优化速度函数单调递增且有上界。

1.2 随机优化速度模型

在传统的优化速度模型中，驾驶员的灵敏度系数始终为同一常数值，不会随着行驶时间的推移而发生改变。但在现实车队的行驶过程中，伴随跟驰行为的持续，驾驶员驾驶状态和驾驶环境出现变化，驾驶员的灵敏度系数也会出现微小的随机变化。考虑一队灵敏度系数随机变化的环形跟驰车流，如图1所示。

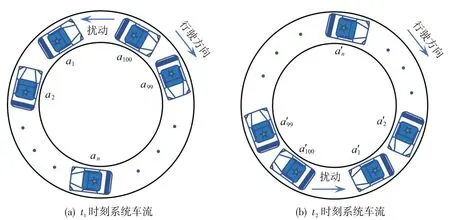
图1 灵敏度系数随机变化的环形车流示意Fig.1 Schematic diagram of circular traffic flow with stochastic change of sensitivity coefficient

图1(a)和图1(b)分别表示系统车辆在t1时刻和t2时刻的驾驶场景。a1,…,an,…,a100为t1时刻系统车辆的驾驶员灵敏度系数；a′1,…,a′n,…,a′100为t2时刻系统车辆的驾驶员灵敏度系数。根据图1描述的车流场景，在跟驰过程中可以将驾驶员的灵敏度系数模型化为一个高斯白噪声过程，建立随机交通动力学方程，得到随机优化速度模型为

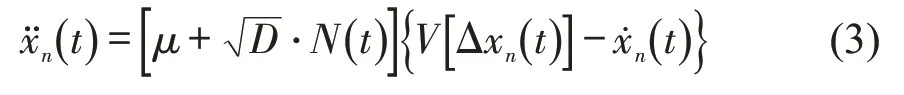
式中：μ为灵敏度系数的均值函数；N(t)为单位高斯白噪声；D为高斯白噪声的噪声强度，在模型中体现为灵敏度系数随机波动的离散程度。

2 随机稳定性分析

交通流的稳定性主要研究扰动对车流演化状态的影响。若系统稳定，扰动会随着时间的推移慢慢消失；若系统不稳定，扰动会随着时间的推移发生传播并增强，引发交通系统的拥堵。在随机优化速度模型中，通过对随机动力方程的转化，在周期性边界条件下，应用随机动力学稳定性理论的矩稳定性分析系统的稳定条件。假设系统车流在初始状态是稳定的，均匀车流的车头间距为b，对应的优化速度为V(b)，此时，稳定交通流的第n辆车位置为

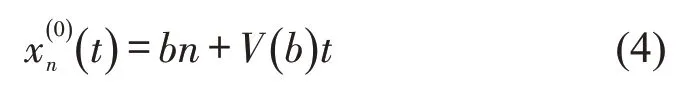
若给车流系统施加一个微小的扰动yn(t)，则第n辆车的位置变为

将式(5)改写为

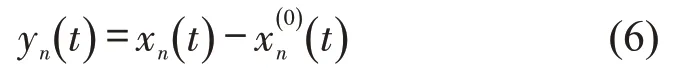
求式(6)的一阶导数和二阶导数，即

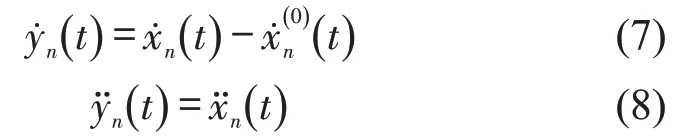
将式(6)～式(8)代入式(3)，对优化速度函数进行Taylor 展开，忽略高阶项后，得到关于yn(t)的SOV模型为

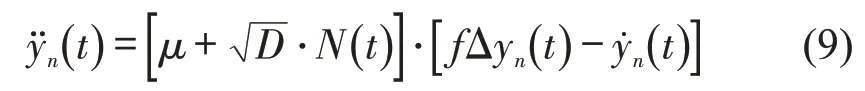
式中：f=V′(b)，V′(b)是V(hc)在hc=b处的导数。

令yn(t)=[φ(t)+ω(t)j] exp(nαkj)，其中，αk=和ω(t)分别为yn(t)的复变幅值的实数部分和虚数部分，然后将yn(t)代入式(9)，令其实部和虚部分别为零，化简为

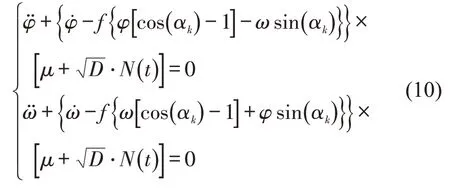
根据随机动力学理论，设W(t)为单位维纳随机过程，单位高斯白噪声N(t)可以看作单位维纳过程W(t)的形式导数，则有

为进行随机动力学稳定性分析，先将式(10)转化为斯特拉多诺维奇随机微分方程，再转化为伊藤随机微分方程。为方便运算，作状态变量转换，令

将式(11)和式(12)代入式(10)，得到的斯特拉多诺维奇随机微分方程，考虑Wong-zakai修正项可以将斯特拉多诺维奇随机微分方程转化为伊藤随机微分方程，即

矩稳定性[10]是随机动力学中常用的判别稳定性的方法，其适用条件包含：受数学或物理白噪声随机过程参激的线性系统；各自的矩方程是线性的；系统方程可以写为伊藤随机微分方程形式。根据上述分析，本文将驾驶员的灵敏度系数模型表示为高斯白噪声，得到式(3)随机模型。施加扰动后将其用Taylor 展开，并忽略其高阶项，得到式(9)参激的线性随机动力学方程。经过代入转化后得到式(13)伊藤随机微分方程，且其各阶方程均为线性方程。因此，矩稳定性分析方法适用于本文模型稳定性的判定。

在实际随机系统中，通常考虑用一阶矩稳定和二阶矩稳定描述随机系统的稳定性，矩稳定性定义为

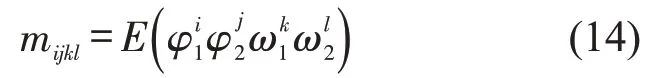
式中：E为求数学期望的表示符；i、j、k、l分别为φ1、φ2、ω1、ω2的阶数。

对式(13)进行一阶矩稳定性计算，其一阶矩形式为

利用式(13)和式(15)求得一阶矩方程

式中：S1为一阶矩方程的系数矩阵；令，得到S1的表达式为

将式(17)转化为特征矩阵，求得特征方程，运用劳斯判据求出SOV 模型的一阶矩稳定性条件，将重复和明显包含在内的条件省略后，得到表达式为

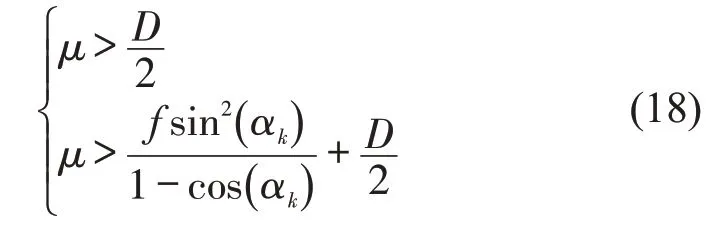
二阶矩稳定性的求解需要用到随机微分方程中的伊藤引理[10]，求解方式与一阶矩稳定性类似，在此不再赘述，SOV模型的二阶矩稳定性条件为

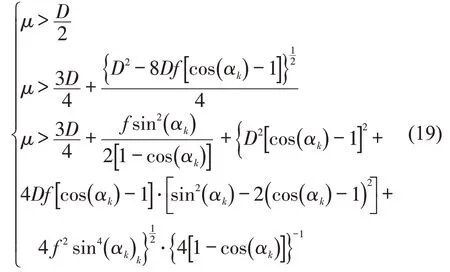
由于伊藤随机微分方程的二阶矩方程维数较高，得出的稳定条件较为复杂。当αk→0 时，可以得到矩稳定条件临界稳定值，此时，一阶矩稳定临界值与二阶矩稳定临界值经过化简后，得到相同的临界值，即

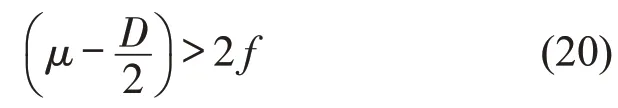
为直观的表达随机优化速度模型的稳定范围，用式(20)和f=V′(b)得到车头间距与灵敏度系数的稳定临界曲线，如图2所示。

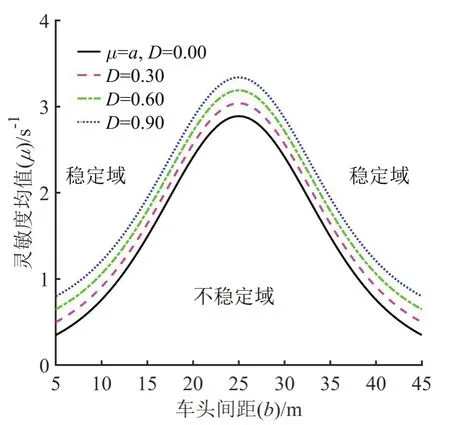
图2 车头间距与灵敏度系数的稳定临界曲线Fig.2 Stability critical curve of headway and sensitivity

由图2可知，SOV模型的稳定范围由灵敏度系数的均值(μ)和噪声强度(D)，以及车头间距(b)共同决定；随着噪声强度的增大，稳定区域会缩小。当噪声强度为零，灵敏度均值μ与OV模型的灵敏度常值系数a相等时，模型退化为确定性的OV 模型，稳定临界条件和稳定区域同OV 模型得到的结论一致。

3 蒙特卡罗模拟

蒙特卡罗模拟是分析随机系统的经典方法，依据随机过程的特性产生样本函数，得到大量的响应样本后可以获得相应的统计量。应用到随机交通动力学方程中，通过模拟车流场景，观察扰动传播的特点进一步了解SOV模型的性质。设循环边界条件，在总长度为L的环形道路上，令车辆总数N=100；初始均匀车流的车头间距为b；初始车速为v(0)，在模拟开始时，给头车一个微小的扰动。

首先，为验证随机稳定性分析中求得的矩稳定性条件，在数值模拟中，设置不同的初始均匀车流的车头间距和车速，以及不同的噪声强度值，观察不同参数组合下系统内所有车辆的车速波动演化，确定数值模拟稳定临界点，形成模拟情形下的稳定临界曲线，如图3(a)所示，数值模拟的稳定临界曲线与矩稳定性分析得到的结果有较好的拟合。为进一步观察拟合情况，设置初始车头间距b=25 m，初始车速v(0)=15.3384 m·s-1，以及初始车头间距b=15 m，初始车速v(0)=3.6413 m·s-1的两个模拟场景，此时f值已经确定。在设定不同噪声强度值后，观察模拟结果，得到两个模拟场景的稳定临界曲线，如图3(b)和3(c)所示，模拟得到的稳定临界曲线有较好的拟合，验证了矩稳定性分析的有效性。在之后的模拟场景中，设置初始均匀车流的车头间距b=25 m，初始车速v(0)=15.3384 m·s-1。

图3 数值模拟与解析解的稳定临界曲线对比Fig.3 Comparison of stability critical curves between numerical simulation and analytical solution

灵敏度系数的噪声强度是研究随机优化速度模型的重要参数，噪声强度代表了灵敏度系数波动的离散程度。为与确定性的OV模型进行对比，在图4(a)中设置OV模型的灵敏度系数a=2.91 s-1，在图4(b)中设置SOV 模型的灵敏度参数为μ=2.91 s-1，D=0.24 s-2。施加同样大小的扰动后，模拟扰动传播过程中300 s 内的车头间距波动情况，如图4(a)和4(b)所示。当SOV模型的灵敏度均值μ与OV 模型的灵敏度系数a在数值上相等时，由于SOV模型中灵敏度系数噪声强度的存在，使得在扰动传播过程中车头间距的波动会比OV 模型更剧烈。

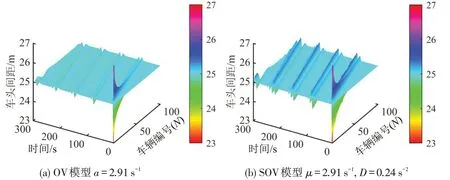
图4 扰动传播过程中车头间距的波动Fig.4 Fluctuation of headway in process of disturbance propagation

然后，在SOV模型中设置不同的噪声强度，图5(a)中设置参数μ=2.91 s-1，D=0.12 s-2；图5(b)中设置参数μ=2.91 s-1，D=0.30 s-2。施加同样大小的扰动后，模拟扰动传播过程中2000 s的车头间距波动情况，可以观察到在图5(a)中，在2000 s里系统车辆的车头间距一直在波动，但在这段时间内的波动并没有明显的加剧，而图5(b)中设置更大的噪声强度后，在2000 s内系统车辆的车头间距波动越来越剧烈，按此趋势最终会使交通系统陷入拥堵。

图5 扰动传播过程中车头间距的波动Fig.5 Fluctuation of headway in process of disturbance propagation

迟滞环是用来描述系统内所有车辆在不同车头间距下，跟驰车速的最大值和最小值所形成的曲线。迟滞环表征拥堵流，因此，迟滞环越大表明系统车流越不稳定，若系统车流在受到扰动后最终回到初始的稳定状态，那么迟滞环最终会缩小为一个点。设置相同的灵敏度系数均值μ=2.92 s-1，设置不同的灵敏度系数噪声强度D=0.05 s-2，D=0.25 s-2,D=0.50 s-2，模拟第5000 s 时刻的迟滞环，模拟结果如图6所示。

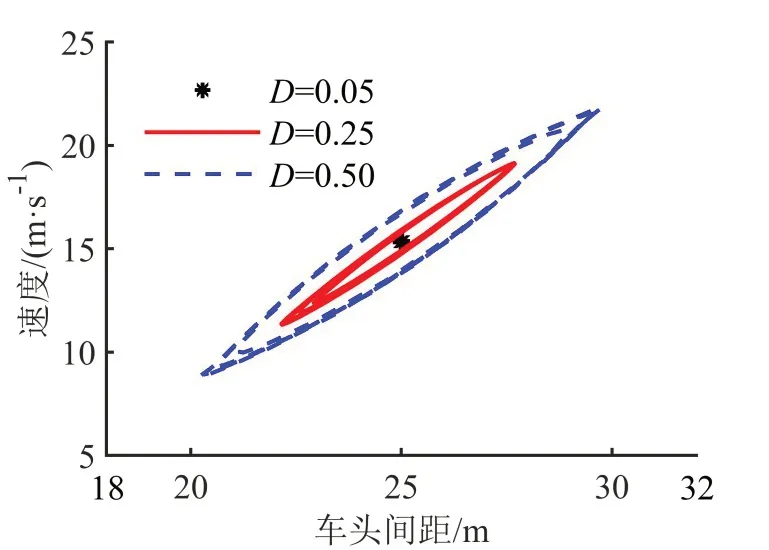
图6 SOV模型不同噪声强度的迟滞环Fig.6 Hysteresisloopsof SOVmodelwithdifferent noise intensity

当D=0.50 s-2时迟滞环最大，系统车流的拥堵最严重。随着噪声强度的降低，迟滞环曲线缩小，当D=0.05 s-2时迟滞环已经几乎缩小为一个点，此时，系统车流变得稳定，车头间距为25 m时所有车辆的车速接近初始速度。

通过与OV模型的对比模拟，以及在SOV模型中设置不同噪声强度进行模拟，说明当灵敏度系数的均值一定时，灵敏度系数的噪声强度越大，扰动传播的过程中会使得跟驰车流更容易产生波动，影响交通系统稳定性。在现实车流中，假设驾驶员的灵敏度系数平均值处于某一水准时，则驾驶员的灵敏度系数随机波动的离散程度会对系统车流的稳定行驶造成影响，即驾驶员的驾驶状态越不稳定，在交通系统受到扰动后系统车流越容易产生拥堵。因此，SOV模型模拟的结果是符合现实车流的合理预测的。

上述分析得到关于灵敏度系数的噪声强度在扰动传播过程中会对系统车流的稳定产生影响。为研究灵敏度系数的噪声强度如何影响扰动传播，在OV模型和SOV模型施加同样的扰动，探究第49辆和第99 辆车的车速波动曲线。图7(a)设置OV模型参数为a=2.91 s-1；图7(b)设置SOV 模型的参数为μ=2.91 s-1，D=0.28 s-2。100～400 s 这个时段，可以观察到SOV模型的车速波动振幅比OV模型更大。

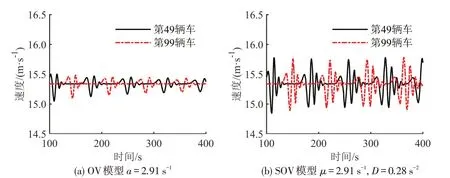
图7 扰动传播过程中车速波动曲线Fig.7 Vehicle speed fluctuation curve in process of disturbance propagation

为更好地说明灵敏度系数的噪声强度对车速波动振幅的影响，设置不同的噪声强度值，在车流中间施加同样的扰动后，以100～400 s 时段内车速波动的标准差为指标反映波动振幅的大小。不同噪声强度下的车速波动标准差如表1所示。

表1 不同噪声强度下的车速波动标准差Table 1 Standard deviation of vehicle speed fluctuation under different noise intensity

由表1可知，噪声强度越大，车速波动的标准差越大，这与图7所观察到的现象一致，表明，如果驾驶员的灵敏度系数发生随机波动，系统车流受到扰动后，时走时停的剧烈程度会增加。

4 结论

本文在优化速度模型(OV)的基础上，考虑驾驶员在跟驰过程中，由于驾驶状态，驾驶环境等原因，驾驶员出现灵敏度系数变化的交通流随机行为，将灵敏度系数模型化为高斯白噪声过程，建立随机优化速度模型(SOV)。根据随机动力学稳定性理论，对随机优化速度模型进行矩稳定性分析，得到SOV模型的一阶和二阶矩稳定性条件的解析解。

对SOV 模型进行蒙特卡罗数值模拟，模拟结果表明：灵敏度系数的噪声强度越大，扰动传播过程中交通系统越容易产生拥堵，具体影响在扰动演化过程中的波动振幅上。灵敏度系数的噪声强度在模型中代表灵敏度系数波动的离散程度，在现实车队中，倘若驾驶员自身驾驶行为出现随机性，驾驶员的灵敏度系数发生随机波动，其波动的离散程度会对交通系统的稳定行驶造成影响。SOV 模型随机稳定性分析的解析解和数值模拟的结果符合现实车流的常理推测。