基于模糊粒子群优化算法的无线传感器网络部署优化研究

张 亮， 黄 郡

(国防科技大学 电子对抗学院，安徽 合肥 230037)

0 引 言

无线传感器网络(wireless sensor networks,WSNs)目前已经被广泛应用到煤矿安全监测、生态环境监测、战场态势感知等众多领域[1]。网络一般由多个无线传感器节点组成，每个节点配备有相应的感知单元、通信单元和能量单元。如何利用这些节点构建一个结构合理、性能优良的网络，也即无线传感器网络的优化部署问题是目前的一个研究热点。无线传感器网络的部署方法可以分为静态部署和动态部署[2]。静态部署指的是在传感器网络运行之前就已经确定各个节点的位置，动态部署则是在传感器网络运行之后还可根据实际情况进行节点移动等位置调整。静态部署又可分为确定性部署和随机性部署。确定性部署指的是通过最优化模型确定传感器节点的最优部署位置，然后将节点部署到指定位置。随机性部署则是将传感器节点随机抛洒到目标区域，然后运用一定的优化算法选择部分节点参与构建网络。与确定性部署相比，随机性部署能够适应目标区域环境恶劣，难以人工到达的场合。

目前针对无线传感器网络的部署问题，研究人员提出了多种解决方法。刘雨博等人利用人工鱼群算法对光纤应变传感网络的优化部署进行了研究，证明优化部署后的结果网络能够比人工随机部署更接近真实值[3]。朱明基于正六边形网格划分，提出了一种变步长节点动态部署方法，可有效延长网络的存活时间[4]。Kulkarni N等人借鉴了确定性部署和随机性部署的思想，提出了一种类随机序列的方法，并对网络的丢包率、平均耗能量、时延等指标在不同的部署方法下的影响情况进行了分析[5]。Fang W等人基于有效克服部署区域空洞的思想，利用空洞维诺图，分别提出了基于空洞中心的部署方法和基于扰动中心的部署方法，取得了较好的目标区域覆盖率[6]。

本文研究随机性部署方法，在标准粒子群优化算法的基础上，通过引入模糊数学的基本思想，并构造调和覆盖率和节点数量之间的目标函数，可实现在使用较少节点数的同时，达到较高的区域覆盖率。

1 问题建模

假定需要覆盖的区域是A，依据网格法，可以将区域A划为m×n个网格，A={a1,a2,…,amn}，划分网格的宽度取决于传感器节点的感知半径r以及所需要达到的计算精度。传感器节点的通信半径为R，参照大部分文献[2]，设定R≥2r。现在有N个传感器节点(S1,S2,…,SN)被抛撒到目标区域A，第i(1≤i≤N)个传感器节点的位置是(xi,yi)。第j(1≤j≤N)个网格的中心为(xj,yj)，则第i个传感器Si到第j个网格aj的距离d(Si,aj)是

(1)

此时，传感器Si对网格aj的感知概率是

(2)

如果考虑噪声干扰、传感器特性等因素，可以取感知概率为[4]

(3)

式中re为传感器节点可测得的不确定度，α1，α2，β1，β2为节点的特异性参数。λ1，λ2的计算公式为

(4)

考虑到所有可能的传感器节点，网格aj被感知的联合概率P(aj)为

(5)

由于目标区域A被划分为m×n个网格，因此区域A的覆盖率P(A)可以计算为

(6)

式中P′(aj)为截断化概率，计算公式为

(7)

在本文中，Pth取值为1，P(Si,aj)的计算使用式(2)。

设计网络优化部署的目标函数为

(8)

式中Seli为第i个传感器节点是否被选中构建网络。当其为1时，表示选中；为0，表示没有被选中。式(8)表示在尽量求得较高网络覆盖率的同时，保证所需传感器数量较少。为了消除P(A)取值为0对除法的影响，并且保证式(8)上下两部分处在一个数量范围内，将其变换为

(9)

此时问题转换为：如何决定哪些传感器参与构建网络，从而使得f取得最小值，下面描述该问题的求解算法。

2 基于模糊粒子群优化算法的问题求解

2.1 符号定义

所有传感器的集合使用S集合进行表示，S={S1,S2,…,SN}。其中：Si=(x,y,sel)，(x,y)代表第i个传感器节点的坐标，sel代表该节点是否被选中参与构建网络。

所有的粒子集合使用X表示，X={X1,X2,…,XP}，P表示候选的粒子数量。每个粒子Xi表示问题的一个可能解，它是一个N维变量，Xi=Xi1Xi2…XiN。Xij表示第i个粒子中第j个传感器是否参与构建传感器网络。

粒子集合对应的速度集合为V，V={V1,V2,…,VP}，Vi=Vi1Vi2…ViN，代表第i个粒子在各个维度上的速度。

2.2 模糊粒子表示

模糊理论目前已经被应用于降水粒子分类[7]、SAR影像变化检测[8]等众多领域，取得了较好的应用效果。传统的集合使用硬规则描述某个元素a与集合U的关系，即a要么属于U，要么不属于。在模糊集理论中，存在一个隶属度函数μ。该函数将每个元素a对应到一个隶属度值μa(U)。该值取值范围为[0,1]，用于描述a归属于U的概率。对应于本文所设计的算法中，粒子Xi的每个分量在迭代更新过程中，也用于描述对应位置的传感器参与构建网络的隶属程度。但为了满足粒子能够在较大的空间范围内搜索，避免陷入局部最优值，本文在更新粒子位置的过程中，并没有限定Xi在[0,1]内，而是在利用该粒子计算适应度函数值时，采用矩形隶属函数[9]将其转换为隶属度，即

(10)

2.3 算法流程

算法输入：目标区域的大小长×宽，粒子数量P，粒子群算法最大迭代次数mIter，传感器的感知半径r，候选的传感器集合S。

算法输出：最佳传感器集合对应的粒子p_best、最佳适应度fit_best，所使用的传感器数量Amount_best。

算法流程：

Step 1 ∥随机生成候选粒子群

生成X和V集合，每个Xi、Vi的各个分量随机取值为[0,1]之间的值。

Step 2 ∥进行迭代寻优

for iter=1:mIter

∥计算当前粒子群各个粒子的适应度

fori=1∶P

forj=1∶N

Sj2等于依据式(10)计算的Xij的隶属度；

基于Sj和式(9)计算此时Xi对应的适应度值fit_temp；

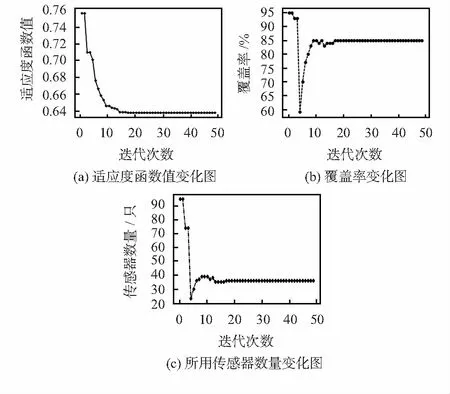
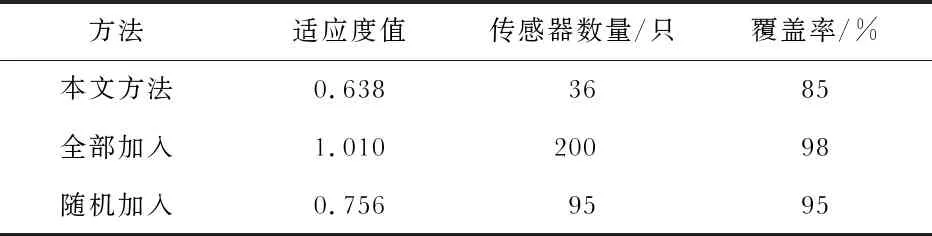
If fit_temp

fit_locali=fit_temp；

p_locali=Xi；

If fit_temp

fit_best=fit_temp

p_best=Xi；

∥更新X和V

fori=1∶P

Vi=w*Vi+c1*r1*(p_locali-Xi)+c2*r2*(p_best-Xi);

Xi=Xi+Vi;

Step 3 ∥计算最优结果对应传感器数量和覆盖率

Amount_best=p_best去模糊化后对应的传感器数量;

Covered_best=(1+Amount_best/N)/fit_best-1。

该算法首先随机生成P个粒子，然后计算每个粒子对应的适应度函数值，并根据该值更新局部和全局最优粒子位置，随后按照粒子群位置更新算法更新粒子的速度和位置，最后输出最优结果。算法中w是粒子群优化算法的惯性权值，c1,c2是对应的学习因子，r1,r2是两个[0,1]之间的随机数。

3 实验与结果分析

3.1 参数设置

设定区域的大小是200 m×200 m，初始随机抛洒的无线传感器数量是200个，无线传感器的感知半径r为20 m。初始生成100个随机粒子，最大迭代周期数是50代。惯性权值w取值为0.6，学习因子c1，c2均取值为2，r1，r2分别取值为0.6，0.3。

3.2 结果及分析

图1是本文方法在求解过程中适应度函数值、覆盖率、所用传感器数量与迭代次数的关系图。

图1 实验结果

从图1(a)可以看出，随着迭代次数的增加，适应度函数值逐渐变优，一直达到一个稳定值，证明本文提出的算法能够解决无线传感器网络的优化部署问题。结合图1(b)和图1(c)可以看出，在初始情况下，大部分传感器节点(95个)都被加入到构建网络中，此时网络的覆盖率也较高(95 %)。但是由于优化部署的目的是在覆盖率和节点数量之间取得一个较好的平衡，此时参与网络的节点数量过多将会导致网络和节点的耗电量和通信量增加、降低网络总体通信效率和存活时间，因此此时适应度函数值比较低(0.756)。随着粒子群优化算法的迭代寻优，覆盖率和传感器数量都经历一个由高到低再到适中的过程，最后取得一个稳定的最优适应度函数值(0.638)，此时传感器数量仅为36个，但是达到了85 %的覆盖率。

表1是本文方法与传感器节点全部加入、随机加入等方法的对比。从表中可以看出：与全部加入、随机加入等方法相比，本文方法的适应度函数值最优，传感器数量仅分别相当于全部加入和随机加入的18 %，37 %，但覆盖率却相当于它们的87 %，89 %，在使用较少节点取得较高的覆盖率方面具有明显的优势。

表1 本文方法与其它方法的对比

在本文中，使用除法式表示式(9)，相当于对覆盖率和节点数量赋予了相同的权重。在实际运用过程中，还可以根据需要将其转换为加法式，并增加相应的权重系数，以决定是倾向于取得较高的覆盖率还是取得较少的节点数量。

4 结束语

本文提出了一种基于模糊粒子群优化算法的无线传感器网络部署优化方法，该方法能够综合考虑网络使用的节点数量和对应的目标区域覆盖率，并通过隶属度函数将连续值转换为01值，从而决定对应的传感器节点是否参与构建网络。实验结果表明：通过多次迭代，该方法的目标函数值能够得到逐步优化。相对于全部加入和随机加入两种方法，该方法在保持较高覆盖率的同时，使用的传感器数量较少。