改进BP算法在混合气体定量检测中的应用*

赵彦如, 黄晓杰, 邵启鹏

(河南理工大学 机械与动力工程学院,河南 焦作 454000)

0 引 言

气体定量识别在食品科学、环境科学、公共安全和国防军事等领域有着广阔的应用前景。文献[1]使用支持向量机算法用于CO浓度的分析；文献[2]使用反向传播(back propagation,BP)算法对单一气体进行定量检测,文献[3]使用BP算法对混合气体进行定量检测,二者均比较了实际、预期和预测的浓度测量值。为了降低BP算法对初始权值和阈值的依赖性,文献[4]使用粒子群优化(particle swarm optimization,PSO)-BP算法对BP神经网络的权值和阈值进行优化,文献[5]使用蚁群优化(ant colony optimization,ACO)算法优化BP神经网络,文献[6]结合布谷鸟搜索(cuckoo search,CS)算法寻优来获取BP算法的最优初始权值和阈值；为了进一步提高CS算法的性能,文献[7]提出了自适应步长的CS算法,文献[8]将解的适应度引入了CS算法,文献[9]提出了自适应步长和发现概率的CS算法,文献[10]提出了混合模拟退火的CS算法。

为解决CS算法可能陷入局部最优值的问题,本文结合以上研究内容,本文提出引入自适应调整发现概率的CS算法和模拟退火算法的BP神经网络用于混合气体的定量检测。用MATLAB软件对实验数据进行仿真分析发现,使用CS算法获得的用于BP网络的初始权值和阈值有一定的可靠性；引入模拟退火算法避免了算法陷入局部最优,与CS-BP算法相比加快了收敛速度；对混合气体中每种气体预测结果的平均相对误差均在10 %左右,达到了预测目的要求,实现了混合气体的定量检测。

1 改进BP算法的提出与实现

1.1 改进算法的提出

针对BP算法依赖初始权值和阈值的问题,提出使用具有强大全局搜索能力的CS算法来获取BP神经网络最优的初始权值和阈值。CS算法的关键参数仅有外来鸟蛋被发现的概率和种群数目,整个算法操作简单、易于实现。CS算法使用由开关参数pa控制的局部随机游走和全局探索随机游走的平衡组合。局部随机游走为

(1)

(2)

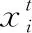
但CS算法存在诸多不足之处：1)在迭代过程中可能会陷入局部最优值；2)在以pa概率发现并放弃解时,算法采用随机方式,即对每个解生成一个0～1之间的随机数,如果该随机数大于发现概率pa,则该解被放弃,这种随机方式可能导致适应度较好的解被放弃,而适应度较差的解得以保留的问题,影响算法的收敛速度和解的质量。因此针对上述问题,利用式(3)判断是否陷入局部最优后采用模拟退火算法机制对布谷鸟的巢穴进行更新,在发现并放弃解时,采用式(4)～式(5),将解的适应度作为评判是否放弃解的一个度量

(3)

(4)

r′i=(ri+pi)/2

(5)

式中pi,hi分别为第i个解的选择概率和适应度,fbest,fworst分别为目前为止最好和最差的适应度。

1.2 改进算法的实现

利用CS算法对神经网络的权值和阈值进行优化。在算法迭代过程中,使用模拟退火操作避免算法陷入局部最优,在此基础上引入发现概率的自适应调整策略用于新解生成；将使BP算法中训练样本的均方误差最小作为目标函数值,再以此优化后的参数作为初始连接权值和阈值用于BP神经网络进行混合气体的定量识别。

Hecht-Nielson R证明了对于任何闭区间内连续的函数都可用具有一个隐层的BP网络来任意逼近[11]。设计了结构为3×6×2的3层BP网络用于实现对混合气体的定量识别。用CS算法对BP神经网络进行优化时,定义每个鸟巢具有的参数分量分别对应于网络的权值和阈值,根据网络结构计算网络中布谷鸟个体的编码长度,权值个数为6×3+2×6=30,阈值个数为6+2=8,所以个体编码长度为30+8=38。即在此算法中,CS算法需优化一个38维的函数,获取该函数的最小值,从而确定BP神经网络中初始权值和阈值的最优值。

算法步骤:

1)初始化相关参数。设置神经网络各层的数目,设寄主的种群数量为n,最大迭代次数为N_IterTotal,步长缩放因子为α,发现概率为pa,需优化的参数个数为nd；

2)随机产生n个具有nd个参数(需要优化的权值和阈值的总数目)的初始巢穴,并产生一个初始的适应度值；

3)对当前鸟巢位置进行莱维迭代：采用Mantegna算法生成服从莱维分布的随机步长,再由式(2)产生新解,遍历每个寄主鸟巢,并计算其适应度值(均方误差MSE),评估解的质量与之前解比较以保留较优值；

4)鸟巢宿主以概率pa发现外来鸟蛋,则根据式(4)～式(5)产生随机数r,若r>pa,寄主选择放弃巢穴,以局部随机游走的方式(式(1))发现新的鸟巢,并评估新解质量,以保留最优解；

5)记录历史最优解,与迭代过程中获得的适应度值对比,选择最优的巢穴位置；

6)当CS算法迭代进行到第12步时,由式(3)判断算法是否陷入局部最优,若陷入,则对鸟巢进行模拟退火操作,计算鸟巢的适应度值,并引入记忆功能保留退火过程中的最优鸟巢位置,退火结束后获取最优巢穴后转入步骤(3)；若未陷入,则直接转入步骤(3)；

7)判断是否满足终止条件,如是否达到最大迭代次数或获得的最小适应度达到了BP神经网络训练的目标值等。若满足终止条件,将获得的最优的解即最优的权值和阈值赋给BP网络作为神经网络的初始权值和阈值后进行网络训练,否则,则跳转至步骤(2)继续迭代直至获取最优化的结果；

8)将经过归一化处理后的传感器阵列的输出电压随机选取一部分作为训练样本,利用BP算法进行网络训练,计算预测输出与期望输出之间的相对误差百分比达到训练目标时,算法结束。一部分进行网络预测,计算神经网络的预期输出与预测输出之间的相对误差。

2 改进算法用于混合气体定量预测

2.1 仿真实验设计

仿真实验中所用数据来自文献[12]。采用酒精的饱和蒸汽和丁烷气体组成混合气体,将TGS813,TGS822和TP—3组成的气体传感器阵列置于容积为5 L的测量容器内,每次注入气体1 mL,即每注入一次气体,浓度增大 200×10-6,测得传感器阵列的输出电压值。测量区域为0～2 000×10-6,再附上浓度为零时的输出值,总共11×11=121组数据。

仿真实验中将传感器阵列的输出电压值作为算法的输入数据,混合气体的浓度值作为输出数据,分别对其进行归一化处理。随机选取98组数据作为训练样本,剩余的23组数据作为预测样本。

实验测试平台为：Windows 10和MATLAB R2014a,主频为2.4 GHz,内存为4 GB。实验中算法的参数设置为：鸟巢数目n=25,步长因子α=0.02,最大迭代次数N_IterTotal=1 000,发现概率Pa=0.25,CS算法中寻优的参数个数nd=38,马尔科夫链长度L=30,BP神经网络的训练目标是0.000 01。

2.2 仿真实验结果及分析

选取剩余的23组数据作为预测样本,采用不同的算法对其进行混合气体的定量检测。

1)不同算法的预测结果对比

仅用单一BP神经网络的预测结果,如图1所示,CS算法优化BP网络(CS-BP)的预测结果如图2所示,改进算法的预测结果如图3所示。不同算法对混合气体预测浓度的平均相对误差对比如表1所示。

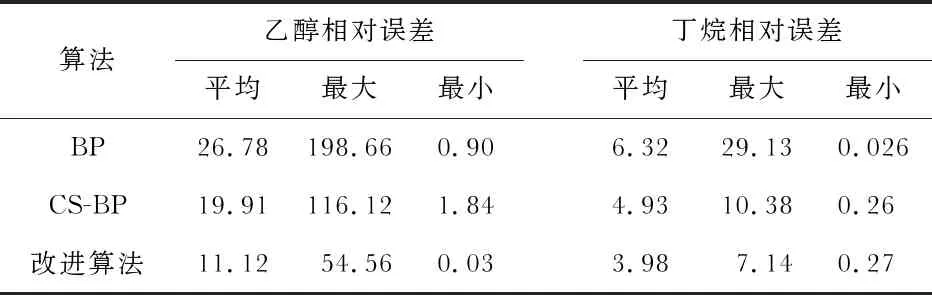
表1 不同算法对混合气体预测的相对误差对比 %

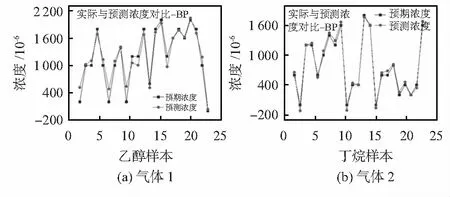
图1 BP算法预测结果对比

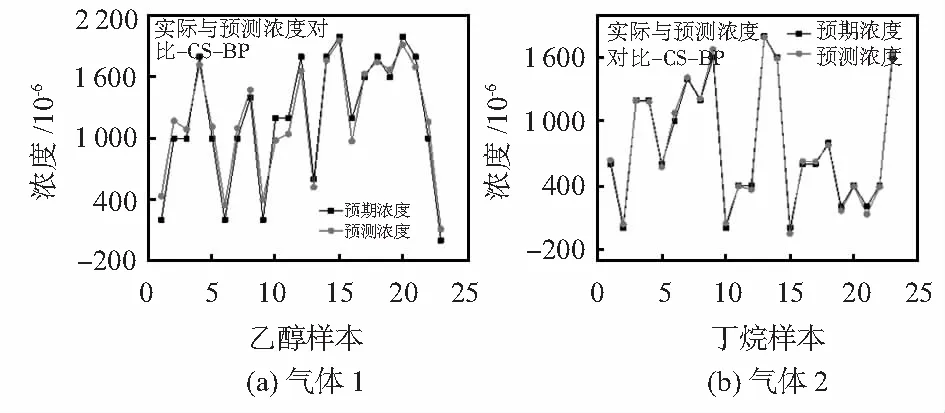
图2 CS-BP算法预测结果对比

图3 改进算法预测结果对比

从图中对乙醇样本浓度值的预测可以看出,仅用BP算法有10个点的预测结果与预期存在较大差距(预测与预期值的相对误差在10 %以上),占总数据点的约43.48 %；使用CS-BP算法有8个点的预测与预期结果之间差距较大,占总数据点的34.78 %；对于改进算法,仅有5个点存在较大偏差,占数据点的约21.74 %,其余18个点的预测结果与预期结果之间差距很小或能够完全吻合,占总数据点的约78.26 %。

对丁烷样本浓度值的预测可以看出,仅用BP算法有4个点的预测结果与预期存在较大偏差,占总数据点的约17.39 %；使用CS-BP算法有2个点的预测与预期的结果存在较大差距；对于改进后的算法,仅有1个点的数据有较大差距,占总数据点的约4.35 %,其余22个点的预测结果与预期结果之间差距很小或能够完全吻合,占总数据点的约95.65 %。从表1可以看出,改进后的算法对预测浓度的三种相对误差整体上相对于前两种算法均有明显减小,且平均相对误差在10 %左右。

2)不同算法迭代过程中适应度变化对比

在迭代过程中适应度随迭代次数变化的曲线图,如图4所示。

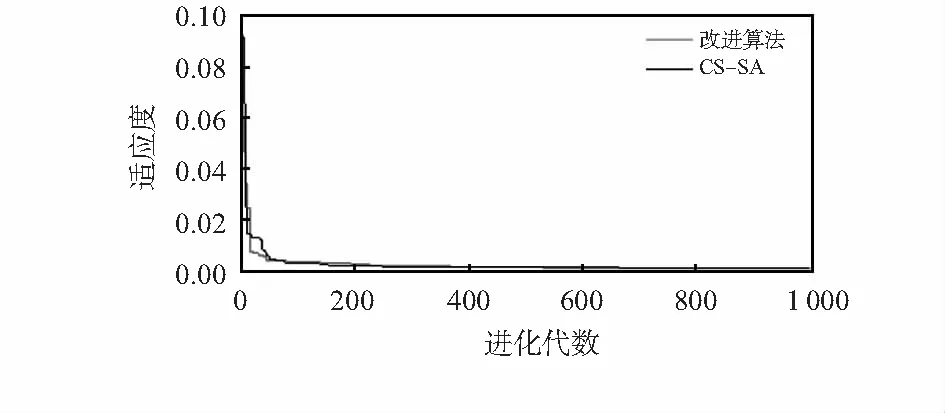
图4 适应度随迭代次数变化的曲线

从图中可以看出,改进后的算法在收敛速度上明显提高,在CS算法的迭代初期,即在第8次迭代时,相较于CS-BP算法,改进后的算法获得的适应度值明显下降,达到最

终迭代次数时，改进后算法获得的最优初始权值和阈值的均方误差较改进前明显减小，CS-BP算法在CS算法迭代过程中获得的最优适应度值即均方误差为0.000 930 72，改进算法在迭代过程中获得的最优适应度值为0.000 765 36，同比减小17.8 %，获得的初始权值和阈值可靠性高。