基于VMD和小波分析的电能扰动信号去噪算法*

冯益林， 余 粟， 王 盟

(1.上海工程技术大学 电子电气工程学院，上海 201620;2.上海工程技术大学 工程实训中心，上海 201620)

0 引 言

随着大功率开关的通断、电力电子器件在电网中的应用，暂态电能质量问题日益严重。电磁脉冲和振荡瞬变以及电压暂升降、突变等成为影响电能质量的主要因素。为了确保电力系统的安全运行，必须有效地检测系统的暂态电能质量。日常工作环境包含了不同种类的噪声，其中大部分为高斯白噪声，对信号特征的识别和提取产生了很大的干扰，因此有效去除噪声是监测电能质量的重要前提。

国内外学者提出如小波去噪算法、S变换、经验模态分解[1](empirical modal decomposition，EMD) 降噪法等，这些方法在电能扰动信号去噪方面得到了广泛的应用。文献[6]对暂态振荡信号和脉冲信号进行了去噪实验，未讨论对其它类型扰动的去噪效果。文献[8]基于EMD算法对信号进行去噪，但EMD本身存在模态混叠、抗噪性能较差[2]等缺陷，从而失真率较高。

本文提出结合变分模态分解[3]( variational modal decomposition，VMD)和小波阈值的算法对采集的含噪暂态扰动信号进行去噪处理，并对去噪效果进行了定量分析，计算信噪比(signal-to-noise ratio,SNR )和均方根误差[4](root mean square error,RMSE)。VMD分解前对信号进行Hilbert变换，计算平均瞬时频率，确定分解层数。小波变换对检测信号的时频域局部信息和奇异点有明显作用，在众多小波基中，db4小波灵敏度更高，适合检测和分析非平稳信号，

更适合电能质量信号的处理[5～9]。分别用EMD算法和传统小波及文献[12]的方法对原始信号进行去噪，对比几种方法的去噪效果。实验表明本文提出的去噪方法不仅能有效去除混杂的噪声，提高了信号特征信息保真率，而且对其它类型的电能扰动信号也有良好的去噪效果。

1 扰动信号的变分模态分解

1.1 算法原理

VMD将一个由多成分组成的实值输入信号分解成多个固有模态函数(intrinsic modal functions,IMFs)[10]，即离散有限带宽的分量。VMD算法在变分框架内构造变分模型并计算约束模型的最优解。每个模态都以函数形式存在，能够调整函数幅频大小并且接近其相应的中心频率。根据信号的频域特性分解信号频带，得到多个固有模态分量。变分问题模型的建立是将信号f(t)分解成K个模态函数uk(t)，使各模态的和与信号f(t)相等，模态分量的估计带宽和值最小，变分约束模型的表达式为

(1)

式中δ(t)为单位冲击函数，{uk}为K个模态函数，{uk}={u1,u2,…,uk};{ωk}为各模态函数的中心频率，且{ωk}={ω1,ω2,…,ωk}。利用增广拉格朗日函数，求变分问题的最优解，表达式为

L({uk},{ωk},λ):=

(2)

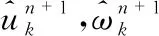
(3)

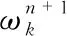
(4)

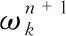
1.2 VMD算法模态数K的确定

利用VMD算法进行去噪处理时，必须确定模态分量的个数K，对信号的频带进行正确的划分。K值设置是否合理直接影响分解结果的精度，若预设K值偏小，则会造成信号成分分解不充分，导致部分有限带宽的固有模态分量不能被分解出来；若预设K值过大，则会过分解原始信号，产生虚假分量，干扰对原始信号中有效成分的分析。

对原始信号进行Hilbert变换得到频谱关系，根据频谱结果进行瞬时频率平均值的计算，确定分解层数K，即

(5)

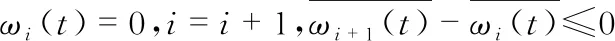
2 基于VMD和小波去噪方法

2.1 去噪原理

提出的VMD结合小波硬阈值对电能扰动信号去噪的方法，首先对含噪信号进行VMD分解，自适应滤除白噪声。由于扰动信号频带较宽，经VMD分解后的多个固有模态均包含原始信号的特征信息。为减少信号能量及特征信息的损失，筛选出含有特征信息的部分模态，重构含噪信号f0(t)。经重构得到的信号较大程度地还原了原始信号，但还包含极少的噪声信息。因为f0(t)噪声含量较少，故采用小波硬阈值法继续去噪。硬阈值函数wλ的表达式为

(6)

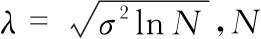
2.2 去噪算法步骤

利用VMD与小波硬阈值算法进行电能扰动信号的去噪：1)利用对采集到的电能扰动信号Hilbert变换，得到功率谱；2)计算平均瞬时频率得到准确的分解层数K进行VMD分解；3)观察固有模态分量，筛选包含特征信息的分量，进行信号重构；4)选用db4小波硬阈值对重构后的低噪信号进行去噪处理，得到去噪后的信号。

3 扰动信号的仿真分析

电能扰动分为六种扰动类型，以电压暂态振荡信号为主要研究对象。用VMD和小波硬阈值结合算法对其降噪，同时选取暂升、中断、脉冲信号三种扰动类型进行了研究。在实验中仿真四种电能质量扰动信号，根据扰动类型的不同设置实验参数，并加入10～30 dB的高斯白噪声。同时与传统小波去噪和EMD及文献[11]去噪方法的去噪效果进行对比。

3.1 扰动信号仿真模型

在影响电能质量的扰动类型中，一般以电压的暂升、暂降、暂断、暂态振荡和谐波为主要方面，模型中以暂态振荡信号为例，ω为角频率，α为振荡幅度，c为衰减系数，t1为振荡开始时间，t2为结束时间，β为常系数,u(t)为阶跃函数，数学模型如表1所示。

表1 扰动信号的数学模型

3.2 扰动信号去噪的仿真分析

3.2.1 暂态振荡信号的去噪

对电压暂态振荡信号进行仿真和去噪处理，设信号的基频均为50 Hz，采样频率设为1 000 Hz，采样个数为1 000个，振荡幅度α=0.4，电压为5 V。在暂态振荡信号中添加10 dB的高斯噪声，得到含噪信号。电压暂态振荡信号如图1所示。

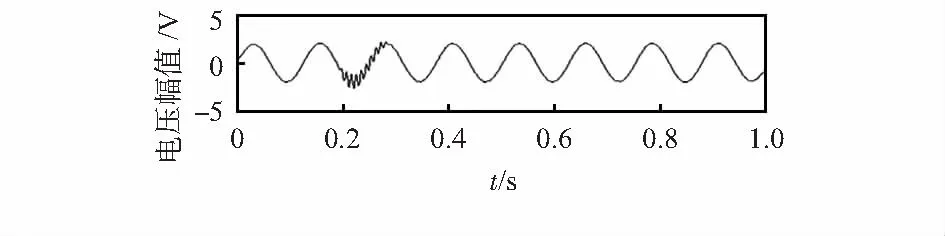
图1 暂态振荡原始信号

经Hilbert变换及计算平均瞬时频率确定VMD分解层数为4，对含噪信号进行VMD分解结果如图2所示。

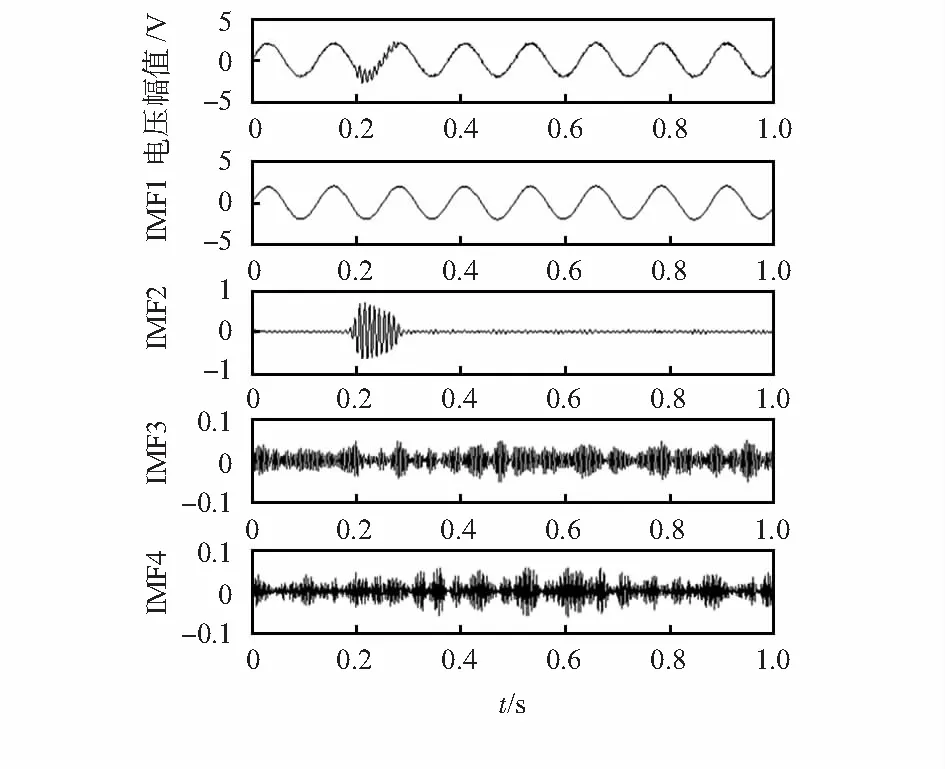
图2 VMD分解结果

观察IMF1和IMF2波形，根据振荡信号的扰动特征全部体现在分量1和分量2中，对特征分量信号进行重构，可见与原始含噪信号的波形的拟合度较高，但仍然包含有少量的噪声，即残余窄带周期的干扰，最后通过小波硬阈值法去噪。重构信号和去噪结果分别如图3。

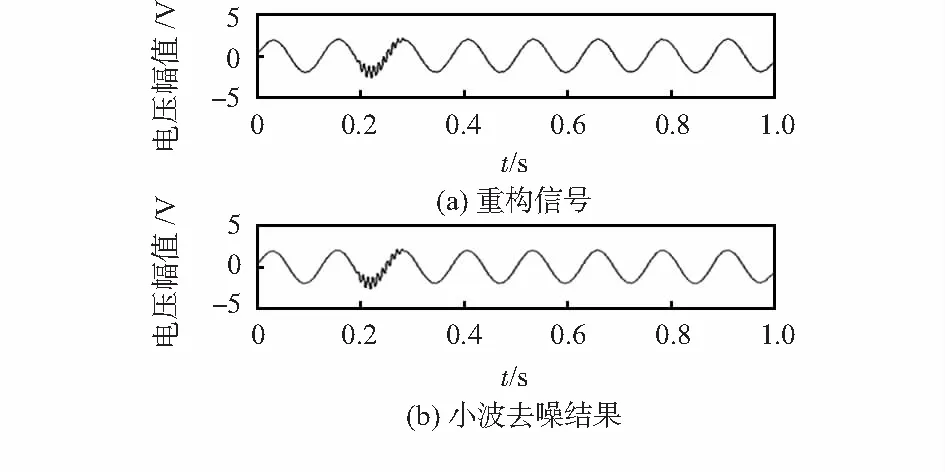
图3 重构信号和去噪结果

3.2.2 电压暂升、中断和脉冲信号的去噪

由于电压暂升和暂降是相对的过程，其特征值也互为相反数，本文选择以电压暂升为研究对象，对暂升、中断和脉冲信号进行去噪，设置信号采样频率为1 600 Hz,采样个数为1 600个,电压为5 V，添加10 dB高斯白噪声，去噪前后效果分别如图4所示。

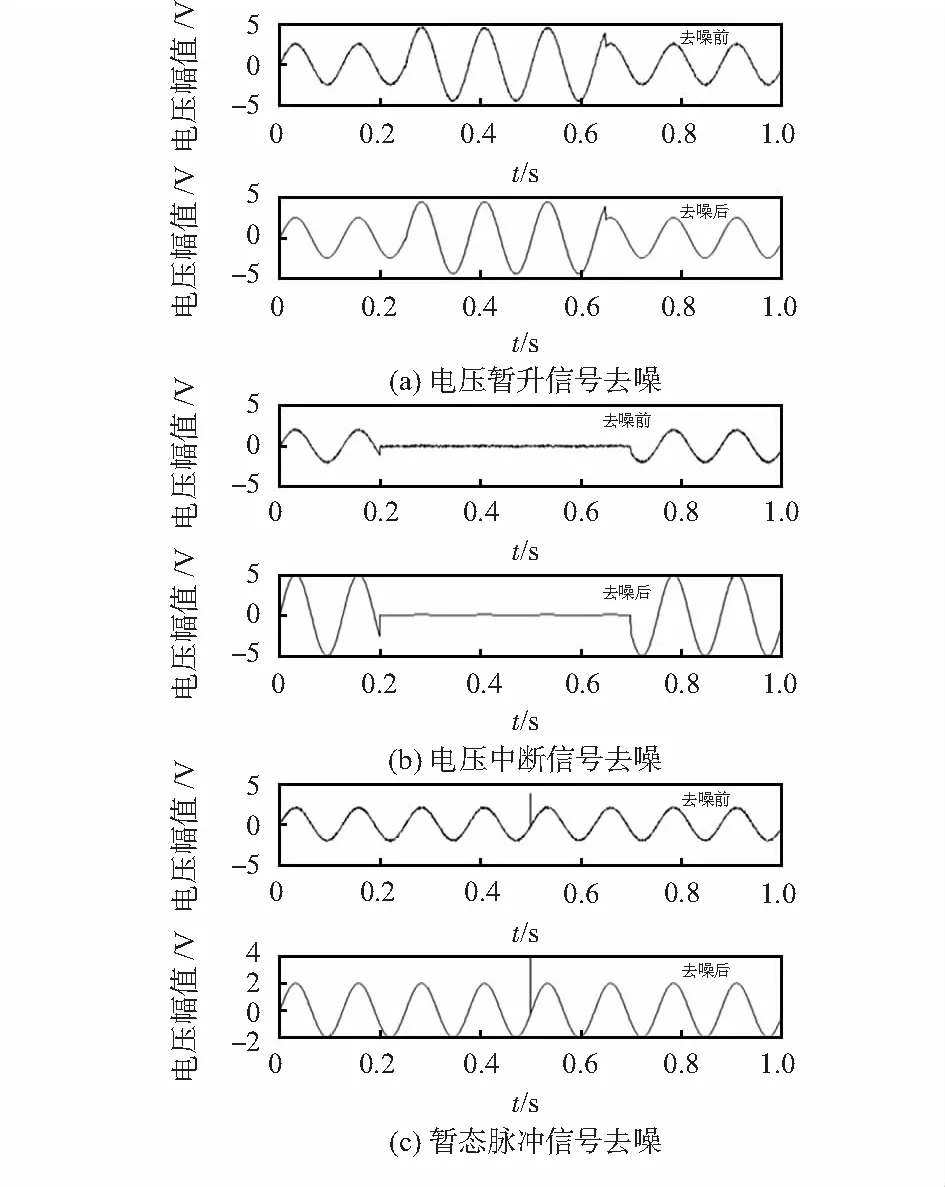
图4 三种状态下的去噪结果

从图4中可以看出经VMD和db4小波硬阈值去噪处理后的信号曲线较为平滑，且去噪后信号的扰动时间与原信号一致，恢复了扰动期间的特征。

3.3 信噪比及均方根误差结果分析

为了更直观观察去噪效果，对扰动信号分别进行定量分析，根据信噪比(SNR)以及均方根误差(RMSE)的定义，对三种去噪算法效果分别进行计算，将计算结果作为去噪效果的评价标准。已知信噪比值越大，均方根误差值越小，算法的去噪效果越好。为确保能对实验效果进行更准确的评估，在相同强度噪声。相同的实验条件下多次试验取其平均值。

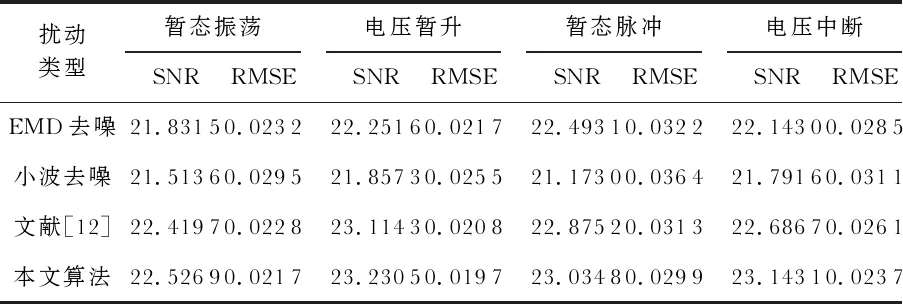
表2 信噪比和均方根误差

从表2中的4组数据可以看出，对于不同类型的扰动信号，EMD去噪效果都优于传统的小波去噪，本文去噪算法的SNR最大，RMSE最小，表明比EMD和小波去噪方法效果更好。

4 结 论

提出了一种基于变分模态分解和小波阈值对电能质量扰动信号的去噪算法。通过计算瞬时频率的平均值，可以准确得到分解模态个数K；VMD分解能够直接排除白噪声的影响，经过对分解后的特征模态分量进行信号重构，再结合小波硬阈值法去噪，得到去噪信号结果良好。与EMD算法，传统小波、文献[12]去噪效果对比，结果表明：本文方法能够更有效地保留原始扰动信号的特征，且始终保持信噪比最大，均方根误差最小，去噪效果理想，为准确提取信号特征提供了一种新方法。