指向“数学眼光”发展的综合与实践
——以“自行车速度里的奥秘”为例
□周静珠
学生往往在应用数学的思想和方法解决问题的过程中,寻求对现实世界现象的认识和理解。数学的眼光由此得以发展。数学眼光是一种意识,一种能敏锐地把实际问题抽象成数学问题的意识;数学眼光是一种思想方法,一种能借助分析、推理,探求事物中隐含着的数学结构的方法;数学眼光是一种综合能力,一种能综合运用所学知识,活学活用的能力。小学数学教材中的综合与实践内容以学生感兴趣的实际问题为素材,引导学生通过数学思考,或构建模型,或给出方案或解决问题,是发展学生数学眼光的好素材。下面以人教版六年级下册“自行车里的数学”为例,谈谈如何基于“综合与实践”活动发展学生的数学眼光。
【案例背景】
“自行车里的数学”是在学生学习了“比例”单元后编排的综合与实践活动,活动以自行车“蹬一圈能跑多远”为研究问题,主要探索“前后齿轮比与自行车蹬一圈行进路程”之间的关系。教学时如果按照教材直接呈现研究问题,引导学生进行探索,会缺少让学生自主发现问题、提出问题的过程。直接呈现问题还会让研究的内容仅限于前、后齿数的比值上,缺少对所涉及知识的综合应用的探究。为此,教师对该活动进行了改造,把“自行车里的数学”改为“自行车的哪些设计与速度有关”,将研究两个问题改成了研究四个子问题(如表1),使研究更有现实价值。

表1
这样的改造使得探究活动更为综合,研究的问题不仅指向比例的知识,更链接了图形的知识,应用图形的特征解释生活现象的原理,应用圆的周长公式解决自行车轮胎大小的问题等等。生活中的实际问题具有复杂性和多样性,改造后的学习设计更贴近真实世界,便于教师引领学生从数学的视角进行观察、分析、建模、解答、反思,发展学生的模型思想、运算能力、应用意识和创新意识。
【案例再现】
(一)数学眼光洞察:经历“现象—问题”的过程
1.情境驱动
播放变速自行车与普通自行车进行竞速比赛的视频。请学生思考:看了这段视频,你能提出什么问题?
2.形成驱动问题
驱动问题:自行车的哪些设计与速度有关?
3.构建研究方案
(1)学生自主提出初步猜想。
影响自行车速度的因素可能有:轮胎大小、脚踏板蹬的速度、自行车的齿轮数、车轮的形状、人骑车的姿势、车轮一周的长度、车把手的形状……
(2)小组讨论筛选最优猜想。
四人小组讨论,针对“自行车的哪些设计与速度有关”这个问题选出最优猜想,形成小组意见(如脚踏板蹬的速度确实能够影响自行车的速度,但是这个因素不属于自行车的设计,因此不纳入最优猜想之中),并全班交流。
(3)学生汇报形成子问题。
通过小组汇报,讨论下阶段研究的方向,形成子问题。
(二)数学眼光论证:经历“猜想—实践”的过程
学生对四个子问题的研究,都经历了“小组共识,聚焦猜想→小组讨论,形成方案→合作探索,验证猜想→构建模型,得出结论”的过程。下面以子问题4“齿轮的设计与速度有什么关系”为例具体展开。
1.小组共识,聚焦猜想
思考:研究“齿轮的设计与速度有什么关系”,可以从哪些方面入手?
想法一:研究前齿轮数、后齿轮数的比值。
学生理由:因为知道齿数和转的圈数成反比例,前齿轮数×转的圈数=后齿轮数×转的圈数=总齿数(不变),所以前齿轮数与后齿轮数的比值就是蹬一圈后齿轮转几圈,后齿轮转几圈,就是后轮转几圈。
想法二:研究车轮的周长。
学生理由:通过观察,自行车是通过脚蹬踏板,带动前齿轮、链条、后齿轮,最后带动后轮转动才往前走的。所以只知道后轮转了几圈还不够,还需要知道车轮周长。
想法三:研究自行车蹬一圈能走多远。
学生理由:要研究齿轮与速度之间的关系,可以先研究蹬一圈,然后通过蹬一圈走多远来推测自行车的速度。
教师建议:研究了前面两个想法就可以研究第三个想法了。
2.小组讨论,形成方案
师:刚才已经讨论出了需要研究的要素,现在要知道它们的具体数据,有什么好方法?
生:可以数一数齿轮数,可以量一量车轮的周长,还可以先测量再计算。(板书:数、量、算)
3.合作探索,验证猜想
教师出示表2,请学生验证猜想。

表2
师:车轮的周长是怎么得到的?
生:通过直接测量车轮的周长;先测量车轮半径,再通过计算得出车轮周长。我们是先测量了车轮的直径,再计算车轮的周长。
师:比值怎样得到?表示什么?
生:这个比值是用前齿轮数除以后齿轮数得到的,是前后齿轮数的比值。
师:周长为什么要去乘前齿轮数与后齿轮数的比值?
生:因为齿轮数与转的圈数成反比例关系,所以前齿轮数与后齿轮数的比值就是前齿轮转1圈,后齿轮转几圈,也就是后轮转几圈。
4.构建模型,得出结论
模型一:前齿轮数÷后齿轮数×车轮周长=蹬一圈的路程
模型二:蹬一圈的路程×单位时间蹬的圈数=单位时间行驶的路程(速度)
(三)数学眼光创见:经历“质疑—创造”的过程
师:如果运用今天所学的知识来设计一辆自行车,你们准备怎么设计?
生:可以把自行车的车轮设计得大一点。
生:那车轮也不能无限大吧!如果车轮很大很大,根本就不能骑了。
生:前后齿轮比大,也就意味着蹬一圈,后轮转动的圈数多。那是否可以让前后齿轮比随意增大?
生:如果前后齿轮比大,确实蹬一圈能够使后轮多转几圈。可是太大了,我们会不会骑不动?
生:变速自行车就是改变了前后齿轮比,每一种行驶的速度都有所不同。
……
【教后反思】
“综合与实践”板块以与学生生活密切相关的各类具有现实性、综合性、实践性特征的问题为抓手,以自主探究为主要学习方式,其教学内容是发展学生数学眼光的重要载体。以“数学眼光”的培育为目标进行教学时,教师要关注以下几点。
(一)驱动问题变“给予”为“内生”,促进数学意识的生长
综合与实践活动以问题为抓手,因而驱动性问题的设计至关重要,一个好的驱动问题能够为学习者提供一个广阔的、多向度的探索空间。它既能激发学生学习的内在动力,也能提纲挈领地为学生指出持续思考、自我探究的方向。
教学实践中,教师容易从知识本位出发,直接把经过加工、改造的问题抛给学生,而忽视了学生自发地从现象中发现并提出自己想要研究的问题的过程。而单纯地让学生漫无边际地提问,也会使研究的方向不清晰。因此,驱动问题的产生,应该是师生共同交流并达成共识的过程,也是学生问题“内生”的过程。
要让驱动问题真正“内生”,首先就要创设一个真实情境,这个情境好比是一个触发器,能够引导学生产生问题,然后在师生的交流中不断让问题聚焦,逐步形成驱动问题。接下来,需要学生根据产生问题的情况提出自己的猜想,并在小组中分析、对比、交流,集中大家的意见,形成研究的主要方向。图1反映了驱动问题“自行车的哪些设计与速度有关”的“内生”过程。学生只有不断经历这样的“内生”过程,才会拥有敏锐的数学眼光,并自觉地去洞察大千世界,从纷繁的表面现象中抽离出数学问题。
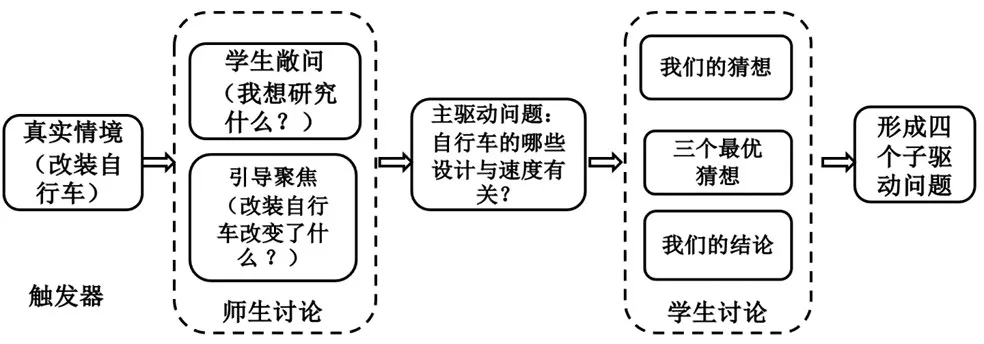
图1
(二)探究过程变“形式”为“实质”,促进数学方法的发展
综合与实践以自主探究为主要学习方式。在探究活动中,如果学生按照教师设计的探究路径一步一步走,那么学生仅仅是一个简单的操作工,而不是独立思考、研究的个体,无法很好地达成对研究过程的感悟,对数学思想方法的体会。同时,如果缺少指导的探究,学生就会无所适从,找不到研究的方向。因此,教师可以从数学问题探究的一般方法入手,找到普适的方法,给予学生指导。
“猜想—研究—结论”是学生解决数学问题的基本步骤。因此,教学中,教师要引导学生先各自进行猜想,然后讨论各自的猜想是否合理,是否指向需要解决的问题,接着根据猜想,开展计数、测量、计算、推理等一系列数学活动,从中感悟方法、提升能力,最后通过探究得到相关的数据,并进一步对这些数据进行分析、综合,逐步形成学习成果——数学结论或数学模型。
探究活动以学生为主体,学生在教师的引导和点拨下,经历科学检验的历程,在全方位的思维活动中达成对数学思想方法的认知,发展数学眼光。
(三)学习评价变“单一”为“丰富”,促进综合能力的提升
教师要引导学生用数学的眼光审视本人和他人在学习过程中的表现,从提出问题、敢于猜想、探索研究、合作交流、达成目标等维度展开自我评价和相互评价。在自评和互评中,学生总结、梳理学习的全过程,推动综合能力的提升。
总之,综合与实践的教学,是引导学生用数学的眼光观察现实世界,从表面现象中抽象出数学问题并进行数学探究的重要渠道。让学生在实践中,养成从数学角度观察现实世界的意识与习惯,提升洞察力、论证力、创造力,就是在培育学生的核心素养,发展学生的数学眼光。

