一题引路 深思而变——对一道教材例题的思考与拓展

文／李 燕

数学教材中的例题都是经过精心挑选的，具有典型性和示范性。若同学们能在学习的过程中认真理清例题的解题方法和所用知识点，并加以拓展，将是实现减负增效的有效途径。下面以苏科版数学九年级下册第25 页的例题为例，谈谈例题的学习与拓展。

【原题呈现】不画图像，判断二次函数y=-x2+5x-8的图像与x轴是否有公共点。

【分析】例题是根据二次函数与一元二次方程的关系，将函数转化为一元二次方程，再利用一元二次方程根的判别式，得到方程实数根的个数就是函数图像与x轴交点的个数。即对于二次函数y=ax2+bx+c（a≠0），当b2-4ac＞0 时，二次函数的图像与x轴有两个交点；当b2-4ac=0 时，二次函数的图像与x轴有唯一的公共点（即顶点）；当b2-4ac＜0 时，二次函数的图像与x轴没有交点。

解：因为一元二次方程-x2+5x-8=0 的根的判别式b2-4ac=52-4×（-1）×（-8）=-7＜0，

所以方程-x2+5x-8=0没有实数根，

所以二次函数y=-x2+5x-8 的图像与x轴没有公共点。

【点评】将函数图像问题代数化，化繁为简，巧妙地体现出二次函数图像与一元二次方程是“形”与“数”的有机结合。

思考一、根据二次函数确定函数中参数的取值范围

【点评】根据抛物线与x轴的交点个数可以确定字母系数的取值范围，其方法是根据抛物线与x轴的交点个数，推出b2-4ac值的性质，即列出关于字母系数的方程（或不等式），通过方程（或不等式）求解。

延伸1 已知二次函数y=x2+x+m，当x取任意实数时，都有y＞0，则m的取值范围是________。

思考二、根据二次函数求一元二次方程中的解及参数

【点评】题面中没有涉及函数图像与x轴的交点个数，但条件y＞0 巧妙地把“数与形”结合在一起，增强了知识联系及延伸，增加了题目深度。

延伸2 已知函数y=（k-3）x2+2x+1 的图像与x轴有交点，则k的取值范围是________。

【解析】当k-3=0，即k=3 时，函数为y=2x+1，此一次函数与x轴有一个交点；

当k-3≠0 时，此函数为二次函数，当b2-4ac=4-4（k-3）≥0，即k≤4且k≠3时，函数图像与x轴有交点。

综上所述，当k≤4 时，函数图像与x轴有交点。

【点评】由于题中没有明确函数是一次函数还是二次函数，因此要分k-3=0 和k-3≠0两种情况进行讨论。

变式2 二次函数y=x2+x-m的部分图像如图1 所示，求一元二次方程x2+x-m=0的解。

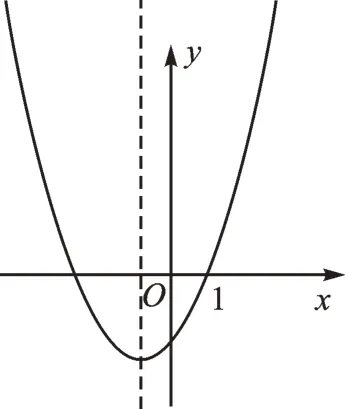
图1

【解析】由图知x2+x-m=0 的一个根为1，所以12+1-m=0，即m=2，故一元二次方程为x2+x-2=0，解得x1=1，x2=-2，所以一元二次方程x2+x-m=0的解为x1=1，x2=-2。

延伸1 已知抛物线y=ax2+bx+c（a≠0）经过点（-1，5），且无论m为何值，不等式a+b≥am2+bm恒成立，求一元二次方程ax2+bx+c=5的解。

【解析】因为不等式a+b≥am2+bm恒成立，所以a+b+c≥am2+bm+c恒成立，所以点（1，a+b+c）是抛物线的顶点，点（-1，5）关于直线x=1的对称点为（3，5）。

当y=5 时，x=-1 或3，所以一元二次方程ax2+bx+c=5的解为x1=-1，x2=3。

故答案为x1=-1，x2=3。

【点评】此题考查了抛物线与x轴的交点及抛物线对称性，找到抛物线的顶点坐标是解题的关键。

延伸2 二次函数y=x2+bx的对称轴为直线x=1，若关于x的方程x2+bx-t=0（t为实数）在-1＜x＜4 的范围内有实数解，则t的取值范围是________。

当x=-1时，y=4；当x=4时，y=8。

t的取值范围为顶点至y=8 之间的区域，即-1≤t＜8。

【点评】把二次函数与不等式转化为两个函数图像的交点问题求解，是解题的突破口，如果能作出图形会显得更为直观。

思考三、根据二次函数确定不等式中的参数取值范围

变式3 抛物线y=ax2+bx+c（a＞0）的图像如图2 所示，则关于x的不等式ax2+bx+c＜0的解集是。

图2

【解析】图像与x轴两交点的横坐标分别为x=-1 与x=2，由图像又知当-1＜x＜2时，图像在x轴下方，所以ax2+bx+c＜0 的解集为-1＜x＜2。

【点评】利用函数图像解不等式。当函数值y＞0时，图像上的点在x轴的上方；当函数值y＜0时，图像上的点在x轴的下方。充分利用数形结合思想，能直观地解决类似问题。

延伸1 抛物线y=a（x-h）2+k（a＞0）经过（-1，2），（5，2）两点，则关于x的不等式a（x-h-1）2+k≤2的解集为________。

【解析】因为抛物线y=a（x-h）2+k（a＞0）经过（-1，2），（5，2）两点，所以大致图像如图3所示：

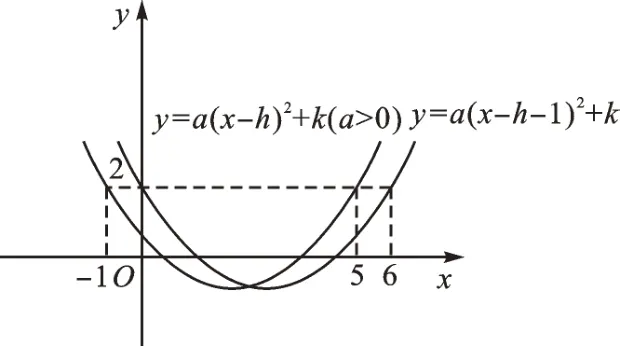
图3

所以y=a（x-h-1）2+k（a＞0）经过（0，2），（6，2）两点，

所以关于x的不等式a（x-h-1）2+k≤2的解集为0≤x≤6。

故答案为0≤x≤6。

【点评】此题考查二次函数与不等式的知识。正确理解数形结合，合理分析是解题的关键。

延伸2 一元二次方程ax2-2ax+c=0有一个根为x=3，且y=ax2-2ax+c过点（2，-3），则不等式ax2-2ax+c≤-x-1的解为______。

【解析】把点（2，-3）代入y=ax2-2ax+c，得4a-4a+c=-3，即c=-3。

把x=3 代入ax2-2ax+c=0，得9a-6a+c=0，则3a-3=0，解得a=1，所以抛物线为y=x2-2x-3。

解方程x2-2x-3=-x-1，得x1=-1，x2=2，所以抛物线y=x2-2x-3与直线y=-x-1的交点的横坐标分别为-1 和2，即不等式ax2-2ax+c≤-x-1的解集为-1≤x≤2。

故答案为-1≤x≤2。

【点评】本题是利用两个函数的图像在坐标系中的位置关系，求自变量的取值范围，可作图利用交点求解，也可把两个函数列成不等式求解。