实验报告:系数对二次函数图像的影响
文/江苏省东台市实验中学“几何画板”社团 王鑫坤
自学教材“二次函数”这一章,我的直觉告诉我,要类比“一次函数”的学习过程。果不其然,老师讲二次函数时,也是从熟悉的、简单的实际问题出发,通过问题中的数量关系引入二次函数的概念,利用描点法画二次函数的图像,用运动变化的观点,由特殊到一般,运用数形结合的思想探索二次函数的图像和基本性质。当看到教材第18—19 页“数学实验室”中介绍“用几何画板软件研究二次函数的性质”后,我尝试自主操作实验,观察系数a、b、c对二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)图像的影响。这里,我将实验操作的过程整理出来与同学们分享。
实验目的:利用几何画板软件画图、动态演示、观察探索、度量计算等,从局部到整体理解二次函数表达式中系数a、b、c对图像的影响,深度理解二次函数。
实验工具:装有几何画板软件的计算机。
实验过程及数学发现:
1.新建可变参数a,画出二次函数y=ax2(a为常数,且a≠0)的图像,如图1,当a>0时,开口向上,对称轴是y轴,顶点是原点。
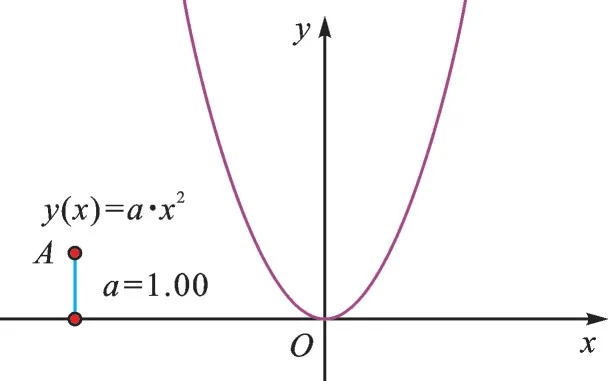
图1
2.改变参数a的值,使它渐渐地变大,并追踪抛物线,如图2,观察发现:它的开口方向、顶点、对称轴都不变,但开口渐渐地向y轴收缩。
3.过y轴上的点作垂直于y轴的直线,交抛物线于E、F两点,改变参数a的值,使它渐渐地变大,并追踪抛物线,如图3,随着参数a的值渐渐增大,线段EF渐渐变短,验证2 的观察结果。
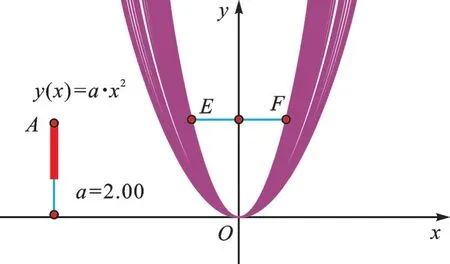
图3
4.过x轴上的点D作垂直于x轴的直线,交抛物线于点P,拖动点D向x轴的正方向运动,如图4,观察发现:当a>0 时,随着点D由左向右运动,在y轴的左边,点P由上向下运动,到原点时,位置最低,越过原点后,在y轴的右边,点P由下向上运动。验证性质:a>0,当x<0时,y随x增大而减小;当x>0时,y随x增大而增大;当x=0 时,y的值最小,最小值是0。
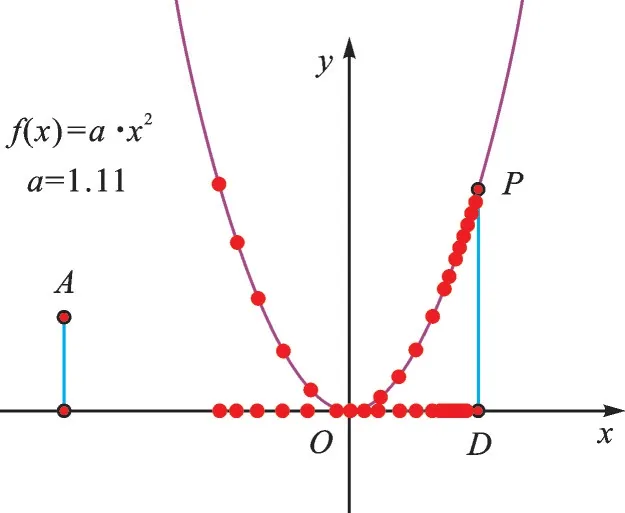
图4
5.改变参数a的值,使它由正变负,渐渐地变小,并追踪抛物线,如图5,我们可以观察到二次函数的图像随着a值的变化而变化带来的直观图像。

图5

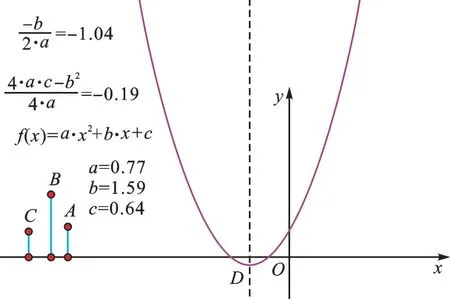
图6
7.只改变参数a的值,追踪顶点D,观察发现:抛物线的形状、位置都在变化,其顶点D在一条直线上运动,如图7。
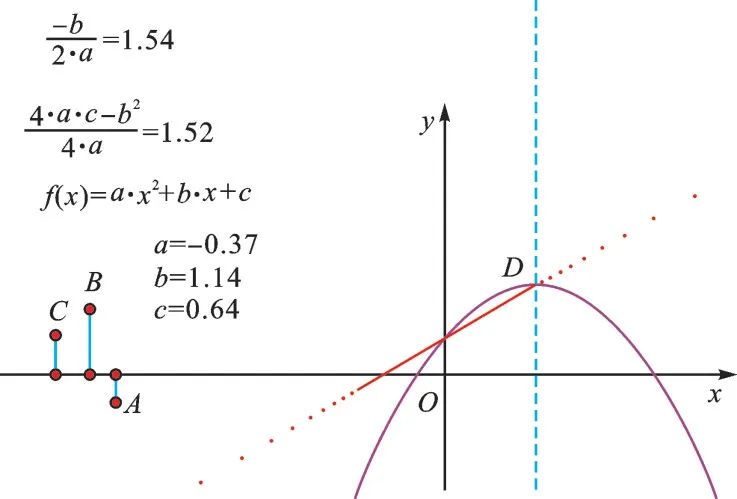
图7
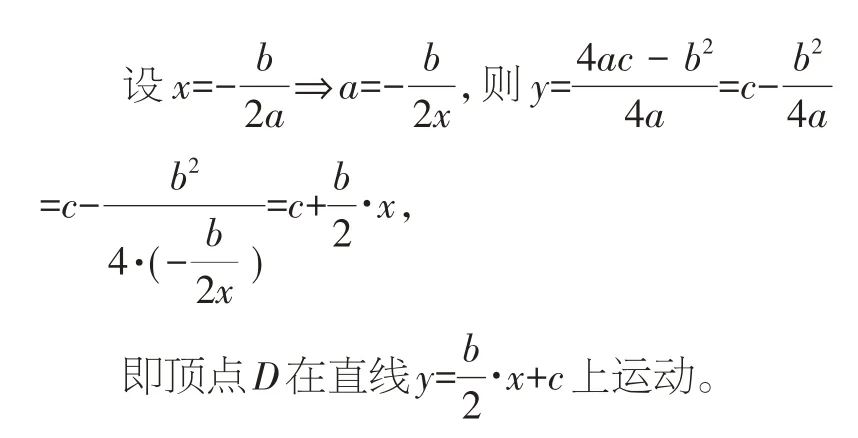
8.只改变参数b的值,追踪顶点D,观察发现:抛物线的形状不变,位置改变,其顶点D在一条抛物线上运动,如图8。
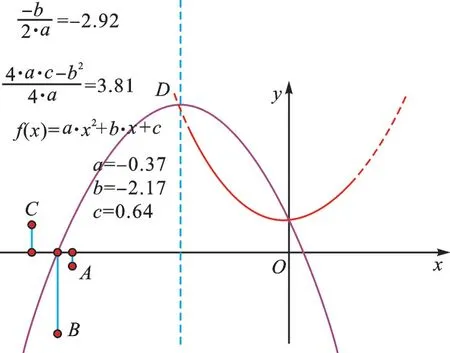
图8

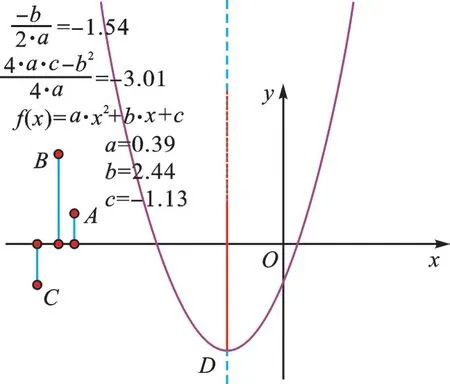
图9
教 师 点 评
王鑫坤同学进入初中后始终对数学保持较高的学习兴趣,在完成学校的学习任务之余,经常主动找数学问题钻研,深入思考,挑战极限,越是难题越能激起他的斗志。几何画板是教师上课引导学生探索新知的重要工具,王鑫坤同学在潜移默化中也学会用几何画板去探索数学的世界。著名教育家苏霍姆林斯基说过:“在人的心灵深处,都有一种根深蒂固的需要,这就是希望自己是一个探索者、发现者、研究者,而在儿童的精神世界中,这种需要特别强烈。”没有什么东西比成功更能增强满足的感觉,也没有什么东西比成功更能鼓起进一步取得成功的努力。王鑫坤同学从数学探索中获取乐趣,我们希望更多的同学主动学习、发现问题、探究问题,实现由“学会”到“会学”,由“会学”到“创新”的目标。

