类比一次函数 生长二次函数

文／曹晓荣

我们知道，形如y=kx+b（k≠0，k、b为常数）的函数叫作一次函数，它右边是一次式，称为一次函数是“名副其实”的。由此我们联想到将右边换为二次式，得到另一个“名副其实”的函数新成员——二次函数，即形如y=ax2+bx+c（a≠0，a、b、c是常数）的函数叫作二次函数。掌握函数表达式与代数式之间的这种联系，有助于我们理解二次函数的概念。

与学习一次函数的路径一样，我们学习二次函数的路径便是这样的。

一、引入概念

从熟悉的、简单的实际问题出发，通过问题中的数量关系引入二次函数的概念，感受二次函数与生活实际的密切联系，既揭示生活与数学的联系，又体现教材前后呼应的整体性。

学习一次函数概念的时候我们曾见过“水滴激起的波纹”这幅图片。二次函数概念的引入也用了这幅图片，只不过我们关注的焦点由“不断向外扩展的圆的周长是该圆半径的函数”，转为“圆的面积是该圆半径的函数”，即C=2πr和S=2πr2。我们通过研究两个函数表达式的差异引出二次函数的概念，然后再通过问题来进一步理解二次函数的概念。

问题1 下列一定是二次函数的是（）。

A.y=2x2B.y=2x-1

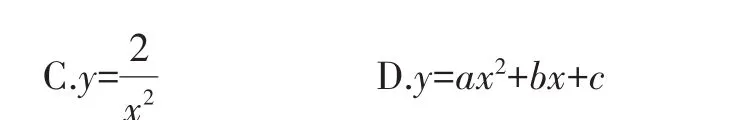
问题2 已知二次函数y=x2-5x+3，则二次项是______，一次项系数是______，常数项是______。

问题3 已知函数y=（m2-m）x2+（m-1）x+m+2。当m满足______时，这个函数是一次函数；当m满足______时，这个函数是二次函数。

通过问题进一步认识二次函数表达式的特征：

（1）函数表达式是二次整式；

（2）二次项系数不能为0；

（3）自变量的最高次数为2次。

二、研究图像与性质

研究一次函数是从列表、描点、连线开始，观察、发现图像和性质，那么研究二次函数的图像和性质我们分三步走：从1开始→从1 到一切→一切从a开始。由特殊到一般，运用数形结合的思想探索二次函数的图像和基本性质。

从1开始——y=x2

通过描点法用平滑的曲线（类比反比例函数图像画法）画出y=x2的图像。

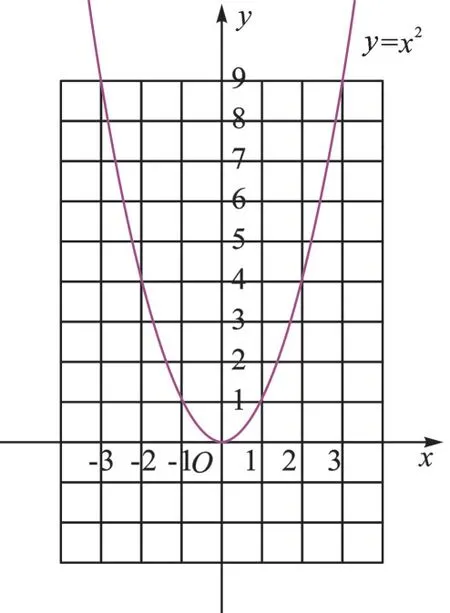
观察图像，初步得出图像的特征：

形状：U型；

对称性：关于y轴对称；

图像趋势：先下降后上升；

最值：最低点为（0，0），当x=0 时，y的最小值为0。

由此了解抛物线及抛物线的顶点、对称轴等。

从1到一切——y=ax2（a≠0）

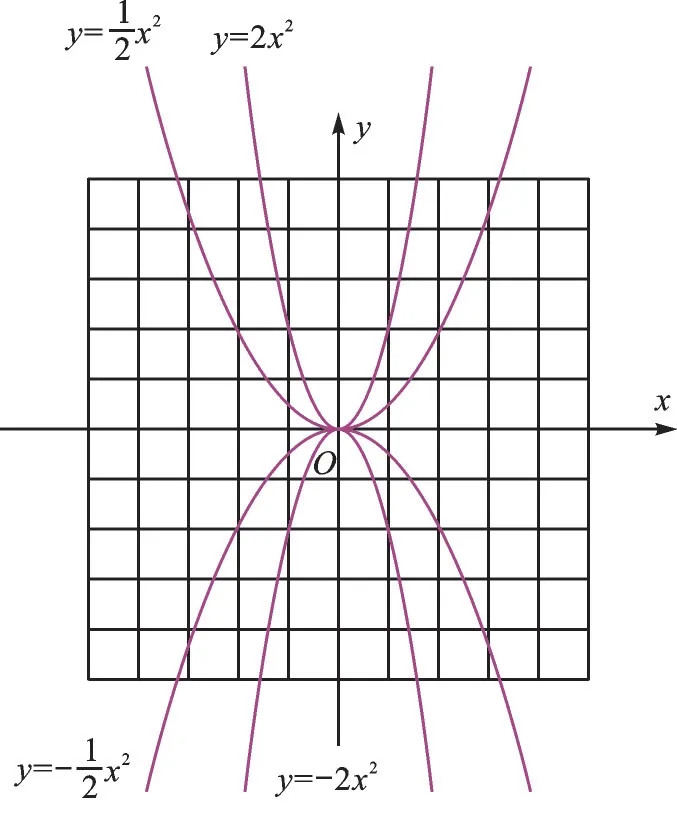
一切从a开始——y=ax2+bx+c（a≠0）

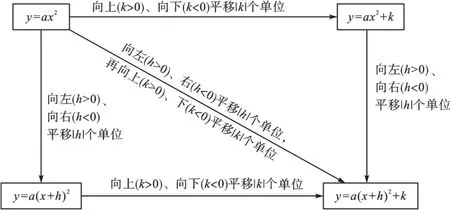
二次函数图像平移小口诀：上下平移在末梢，左右平移在括号；上加下减，左加右减。

三、类比学习

从函数的视角出发，审视一元二次方程与二次函数的关系，借助图像的直观性，探索使函数值y为0 时自变量x的值，进而得到用二次函数的图像求一元二次方程近似解的方法，领悟无限逼近的重要思想方法。

二次函数y=ax2+bx+c（a≠0）的图像与x轴的交点的横坐标是一元二次方程ax2+bx+c=0（a≠0）的实数根，函数图像与x轴的交点情况可由对应方程的根的判别式b2-4ac与0 的关系来判断。用二次函数y=ax2+bx+c（a≠0）的图像估计一元二次方程ax2+bx+c=0（a≠0）的根时，一元二次方程的根就是二次函数图像与x轴的交点的横坐标的值。

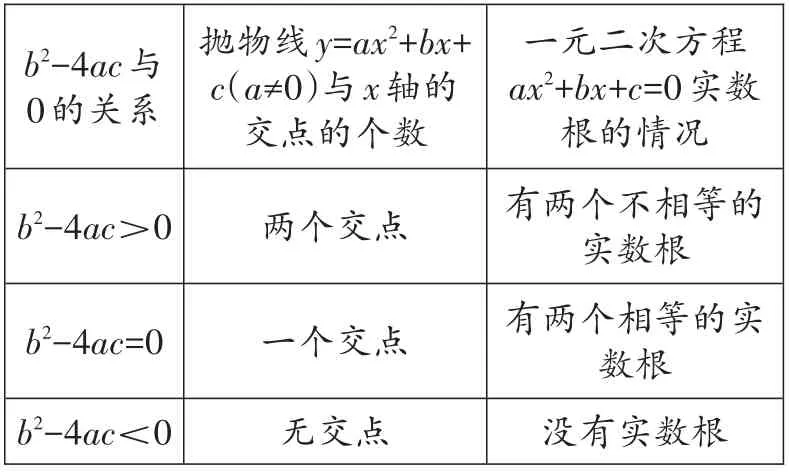
b2-4ac与0的关系b2-4ac＞0抛物线y=ax2+bx+c（a≠0）与x轴的_____________交点的个数两个交点b2-4ac=0 b2-4ac＜0______一个交点无交点________一元二次方程ax2+bx+c=0实数根的情况____有两个不相等的实数根_____有两个相等的实数根______没有实数根___

抛物线y=ax2+bx+c（a≠0）与直线y=kx+m相交于点M（x1，y1），N（x2，y2）（x1＜x2），当a＞0 时，不等式ax2+bx+c＞kx+m的解集是x＜x1或x＞x2，不等式ax2+bx+c＜kx+m的解集是x1＜x＜x2；当a＜0 时，不等式ax2+bx+c＞kx+m的解集是x1＜x＜x2，不等式ax2+bx+c＜kx+m的解集是x＜x1或x＞x2。

进一步思考，由二次函数y=ax2+bx+c（a≠0）的函数值y＞0（或y＜0），即可得到一元二次不等式ax2+bx+c＞0（或ax2+bx+c＜0），此时确定不等式的解集就转化为求抛物线位于x轴上方（或下方）时对应点的横坐标的取值范围。如抛物线y=x2+4x-5 位于x轴上方时对应点的横坐标的取值范围是x＜-5 或x＞1，则不等式x2+4x-5＞0的解集是x＜-5或x＞1。

问题 若二次函数y=x2-4x+n的图像与x轴只有一个公共点，则n________。

【解析】与x轴只有一个公共点，则b2-4ac=0，可得n=4。

变式1 若二次函数y=x2-4x+n的图像与坐标轴只有一个公共点，则n________。

【解析】由题意知图像与x轴没有公共点，则b2-4ac＜0，可得n＞4。

变式2 若二次函数y=x2-4x+n的图像与坐标轴有两个公共点，则n________。

【解析】由题意知图像与x轴只有一个公共点，则b2-4ac=0，可得n=4；当n=0 时，图像过原点，则其与坐标轴有两个交点，所以n为0或4。

变式3 若函数y=nx2-4x+1 的图像与坐标轴有两个公共点，则n________。

【解析】当n≠0时，图像与x轴只有一个公共点，则b2-4ac=0，可得n=4；当n=0 时，一次函数y=-4x+1与坐标轴有两个公共点，所以n=0或4。

变式4 若二次函数y=x2-4x+n的图像与坐标轴有三个公共点，则n________。

【解析】图像开口向上且与坐标轴有三个交点，则图像一定与x轴有两个交点且不过坐标原点，由Δ＞0且n≠0可得n＜4且n≠0。

变式5 若函数y=nx2-4x+1 的图像与坐标轴有三个公共点，则n________。

【解析】当n=0 时，一次函数y=-4x+1 与坐标轴只有两个公共点，不符题意，所以当n≠0 时，图像一定要与x轴有两个交点，由Δ＞0且n≠0可得n＜4且n≠0。

我们通过类比学习，可以了解知识的发生、发展过程，找到学习函数的通法，不仅能在学习二次函数的过程中理顺思路，明晰关系，深化理解，还能为以后的函数学习奠定基础。