基于频率分解的平面图像色彩增强方法

胡 奡

(桐城师范高等专科学校 商贸与电子信息系，安徽 桐城 231400)

图像色彩增强是最基本也是最关键的图像信息处理技术，交通监控、医学影像、刑侦技术以及军事领域都有其应用范围.未经处理的原始平面图像可能存在噪音干扰，包括光照条件、天气原因、物体本身反射性质等因素均会使图像清晰度不够，色彩饱和度不够，细节信息缺失，导致灰度值小，亮度过高，图像模糊不清等问题.为使这些问题能够得到很好的解决，相关专业人士做过很多探索和研究.例如，刘玉红[1]等人提出眼底彩色图像增强方法，虽然可以实现色彩的增强，色泽和亮度都有效提升，但在计算时需要人为地设定参数，导致计算繁琐，不具有适应性.黄冬梅[2]等人探索利用直方图增强图像，该方法的自适应较强，但当原始图像存在灰度动态范围小，分布不均时会使图像细节损失，甚至有噪声被放大的现象.频率分解可将图像不同层次的细节分量划分成空间内的频率，依据不同频率对图像实施增强可提升图像视觉效果[3-4].基于此，本文提出了一种基于频率分解的平面图像色彩增强方法.将平面图像的RGB色彩空间转化成HSV空间，获取色度、饱和、亮度分量，利用自适应二维经验模式分解方法分解各个分量，获取区域Retinex入射光分量后，使用Retinex算法计算照射分量，并通过入射光、反射光图像以及Retinex算法输出的校正，得到适应视觉特征的优质结果，经全局HSV色彩空间修正，保证图像全局色彩的理想化后，将HSV空间模型转回RGB空间，实现平面图像色彩增强.对于整体和局部的平面图像增强后，色彩饱满，图像清晰，有效地解决了因亮度和对比度较低导致的细节信息丢失问题，效果明显，应用广泛.

1 基于频率分解的平面图像色彩增强方法

1.1 Retinex算法

Retinex算法基于视觉对亮度和色彩的感知，并通过感知到的色彩和亮度自动调节，保证色彩持久[5].区分平面图像的照度变化和表面变化的原因是入射光亮度导致的色彩变化相对于物体表面反射导致的变化程度缓慢.以此可得出入射光与反射物相互作用组成的平面图像[6].

Retinex算法中，入射光和反射属性可以用如下数学表达式表示.

f(x,y)=l(x,y)×r(x,y)，

(1)

其中，原图像是f(x,y)，入射光和反射光图像分别是l(x,y)和r(x,y).

从公式(1)中可以计算出反射光图像，

R=F-L，

(2)

其中，R=log(r),F=log(f),L=log(l)分别代表反射光图像，原图像与入射光图像取对数的结果，结果即是R指数函数.

1.2 自适应二维经验分解

自适应二维经验分解(ABEMD)是通过多尺度架构的优化方法，将一维信号转换为二维信号[7-8].再结合二维内蕴模式函数采集图像极值点，将极值点曲面插值，计算包络面上的平均值[9].然后利用二维内蕴模式函数减去二维信号，得到的值就是趋势函数，最后进行迭代.f(x,y)(x=1,…,M,y=1,…,N)表示M×N大小的图像信号，要将原图像分为高频率和低频率两部分二维内蕴模式函数[10]，可利用自适应二维经验模式分解完成.分解后的图像尺度对应的频率依次递增排序，即完成细节模式搭建.进行分解时，要保证二维内蕴模式函数与自身均值为0的初始二维信号相称、极大值点与极小值点分别为正、负.公式(3)表示的是分解结果

(3)

式中，bimfk(x,y)用于描述第k层的二维内蕴模式函数图像，经过N层划分获取趋势图像rN(x,y)/

1.3 Retinex算法与自适应二维经验模式分解结合

利用高斯卷积对原始平面图像的入射光分量计算，采用中心环绕Retinex算法.这一过程要考虑尺度的选择.采用单一尺度Retinex算法，会侧重于局部，采用多尺度Retinex算法，会因运算量的加大而有效率变低[11].另外，在设定单一尺度与多尺度时，结果会因环境的不同而不同.通过本文的自适应二维经验模式分解方式采集入射光分量时，会依据图像原本特征自主配对尺度，运算方式非常简单.

使用自适应二维经验模式分解后获得几个不同尺度的二维内蕴模式函数图像与趋势图像，分别概括了不一样的频率特征.在估算入射光分量时，由于自适应二维经验模式分解可自主配对尺度，可使对细节的采集区域最大化，所以删掉细节信息，例如图像噪声，即是高频分量.在接下来的Retinex算法计算过程中不会出现“光晕”现象的原因是在这过程中照度分量可以直接反映出光照信息.

1.4 算法流程

能够有效确保平面图像后续处理的繁杂程度低和图像增强效果好是实现平面图像处理最优方法，本文所提方法是基于频率分解平面图像色彩增强方法，其具体框架见图1.

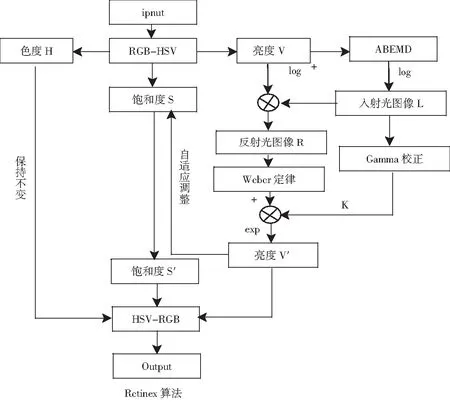
图1 本文增强算法框架

变换图像RGB空间为HSV空间，再对各分量用Retinex算法进行分解，最后通过Retinex算法校正适应入射光和反射光分量.加权获取增强处理后的亮度分量可以将R、G、B三个通道简化成单通道计算，以增强后亮度分量V′为依据校正饱和度分量S，而色度分量要与之前一致，这样可以保持彩色图像颜色不失真，最后将其转化成RGB域[12-13].

1.4.1 区域Retinex入射光图像采集

区域Retinex入射光图像采集是实现图像色彩增强的核心，这里应用自适应二维经验模式分解，将图像分解成k层后，获取区域Retinex入射光分量，具体步骤为如下.

(i)将原图像f(x,y)实行直方图的平均化，转换色彩空间，得到色度Horg、饱和度Sorg和亮度Vorg三个量.

(ii)在不一样的光照条件下将亮度分量Vorg提高，得到n1,n2,…,nm照射系数，获得m幅图像Vorg1(x,y),Vorg2(x,y),…,Vorgm(x,y).

(iii)通过自适应二维经验模式对平面图像Vorg分解，将Vorg1(x,y),Vorg2(x,y),…,Vorgm(x,y)分成k层，其中，高频分量是imfij，低频分量是pih(x,y)，即分解获取的区域Retinex入射光分量.

1.4.2 基于Retinex算法的校正

对于Retinex算法获得的入射光和反射图像以及输出结果，为得到适应视觉特征的优质结果，可用如下步骤进行校正.

(i)校正入射光图像

利用Gamma校正入射光图像解决光照不均导致亮度明暗不均的问题[14].为使其自适应性加强，利用公式(4)进行变换获取校正完成入射光图像，

y(i)=ia·i+a，

(4)

式中，像素值是i，像素为a，其范围为{0-1}.变换后，可以达到增强低亮度区域效果的同时控制高亮度区域的严重曝光，达到全局增强的目的.

(ii)校正反射光图像

若符合临界可见偏差，针对改善反射光P图像对比度的区域清晰程度，可利用Weber定律校正反射光图像[15].通过视觉辨别出两个亮度值差与背景比值，即光强I在1—1000 cd(坎德拉).用公式(5)表示，

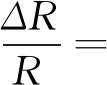
(5)

式中，R为反射光图像，ΔR为反射光图像临界可见偏差.

优化计算量使物体边缘和表面匹配度更佳，用公式(6)表示，

(6)

算法修正后的反射光图很好地协调了图像局部细节与增大全局图像亮度对比度.同时，因为有自适应的特征，因此不需要考虑提前设置数据.

(iii)Retinex算法输出校正

为了能真实地呈现出客观影像，改进中心环绕Retinex算法，产生的增强后图像仅具备较窄亮度范围问题，改进公式如(7)，

(7)

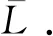
1.4.3 全局HSV色彩空间修正

增强处理平面图像亮度分量会在一定程度上变更饱和度和亮度之间的匹配度，影响图像色感.为保证全局色彩的理想化，饱和度分量要有如下的自适应调整.调整方式如公式(8).

s′(x,y)=s(x,y)+t(υ′(x,y)-υ(x,y))×λ(x,y)，

(8)

式中，

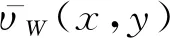
加入系数λ，V分量的变化结果会影响S分量.λ的值越大，则表示S分量受V分量影响越大.根据公式(9)，H、S和V分量被转换成R、G和B分量，输出最终结果.

(9)

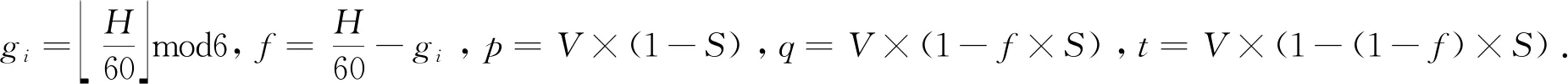
2 实验分析

为了验证本文方法的有效性，利用MATLAB平台，测试图像的帧率为30 fps，分辨率为800×600的环境下，通过DSP平台进行仿真对比实验.本文以平面图像数据库中的图像为例，随机选取图片进行实验.实验的具体流程如图2所示.

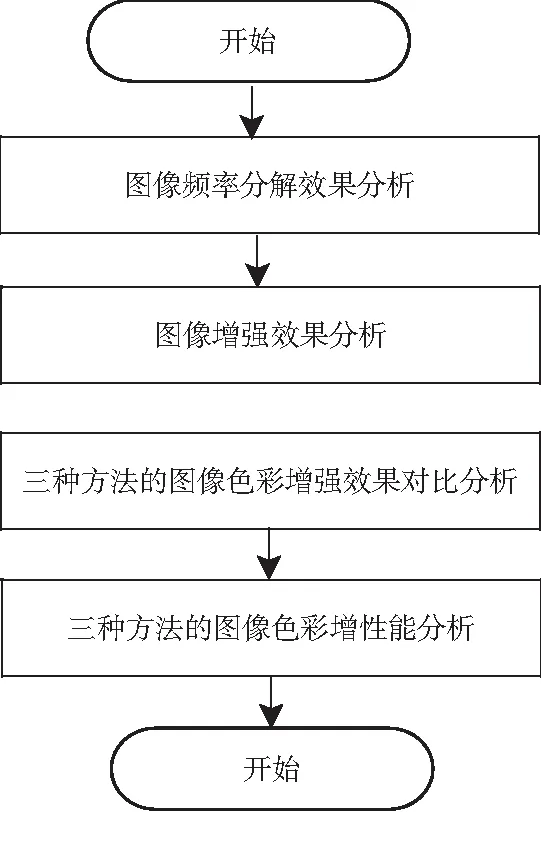
图2 实验的具体流程图

本文先随机选取平面图像原图，对图像高低频进行分解处理，分析图像频率分解效果；从实验数据库中随机选取一张平面图像，采用本文方法对该图像进行图像增强处理，分析图像增强效果；并验证本文方法、文献[1]方法和文献[2]方法的图像色彩增强效果；以平面图像的均值、方差、信息熵和清晰度4个评价指标为实验指标，分析本文方法、文献[1]方法和文献[2]方法的图像色彩增强性能.

2.1 图像频率分解效果分析

图3(a)是随机选取平面图像原图，图3(b)和3(c)分别是经过低频分量处理和高频分量处理的平面图像.从图3相应的图片信息可判断出，低频分量中信息详细，高频分量中高频细节突出，说明使用本文方法可以实现平面图像高低频分解，效果明显.

图3 高频与低频分解的平面图像

2.2 图像增强效果分析

从实验数据库中随机选取一张平面图像，见图4(a)，采用本文方法对该图像进行图像增强处理，处理后的效果图见图4(b)，本文方法图像增强处理前后的直方图均衡化效果图见图5.

图4 本文方法图像增强前后效果图

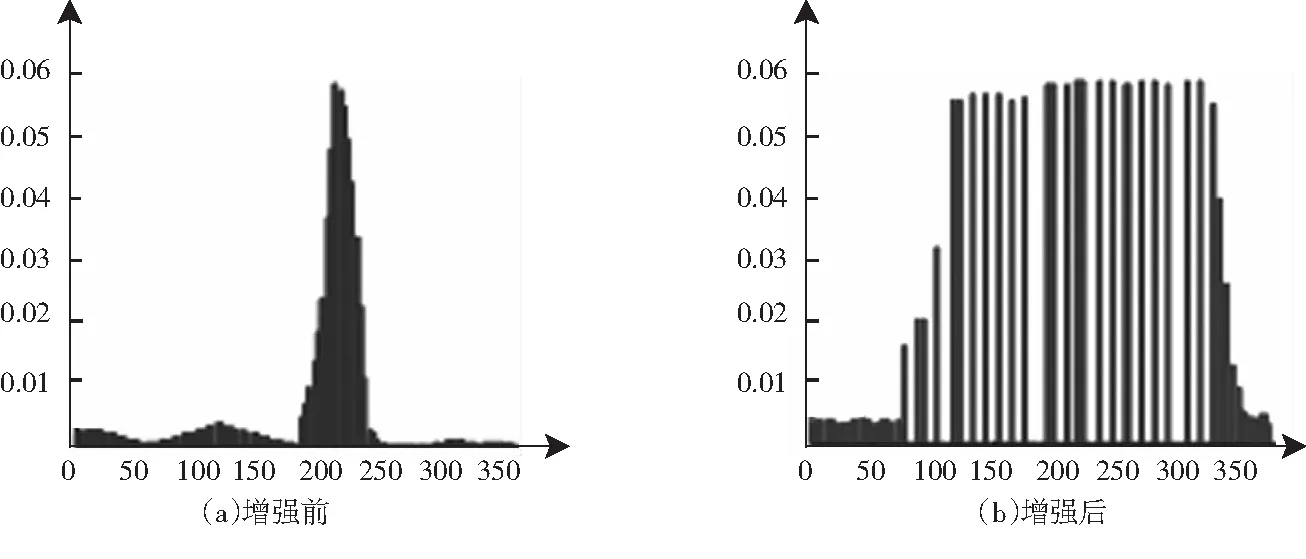
图5 本文方法增强前后直方图结果

本文所提方法处理的图像结果，除了达到平面图像增强的效果，还彰显出图像背景的细节，减少图像噪音.在灰度直方图中，使每一个像素点在合理范围内分布，且不会减少灰度层次，图像均衡化效果较好.

2.3 图像色彩增强效果对比分析

实验图像为从图像数据库中随机选用的flower和street实景平面图像，分别利用本文方法和文献[1]的眼底彩色图像增强方法和文献[2]的自适应直方图增强方法对受到不同因素影响的2组平面图像进行增强，分析其处理因图片色彩、清晰度和细节信息因光照、对比度和动态范围等因素造成的问题图像的能力.其中，(a)为原图，(b)为本文方法处理结果，(c)和(d)分别是文献[1]和文献[2]方法处理结果，具体如图6和图7显示.

图6 flower实验结果

图7 street实验结果

综合图6和图7所示处理结果可以看出，文献[1]方法处理后，整体色调发灰，即使亮度有些变化，但对比度没有明显改变.而用文献[2]方法处理后，整体亮度过度，导致图像信息明显的失真.即使色彩的恢复保持得很好，但难以保证图像的特征不会被改变.用本文方法进行增强处理后，图像暗区的色彩与细节均能被完整地复原.实验结果表明，本文方法处理后，图片亮度合适，色彩饱和度高，细节能够真实地呈现出来，局部对比度合适，清晰度高.

2.4 图像色彩增强性能分析

实验通过平面图像的均值、方差、信息熵和清晰度4个评价指标，衡量本文方法图像增强效果，评价指标值越大图像增强效果越好.

用公式(10)表示信息熵，

(10)

用清晰度评价图像的清晰程度，用公式(11)表示，

(11)

式中，M×N表示图像的大小，ΔIx和ΔIy是像素点在x和y方向上的差分.

利用上述公式计算图像子块上的均值、方差、信息熵与清晰度时，把平面图像均分成10×10的像素块，算出RGB色彩空间中的每个通道每个子块的均值，再计算平均值.将计算结果在0～1的范围内归一化处理.结果用表1表示.

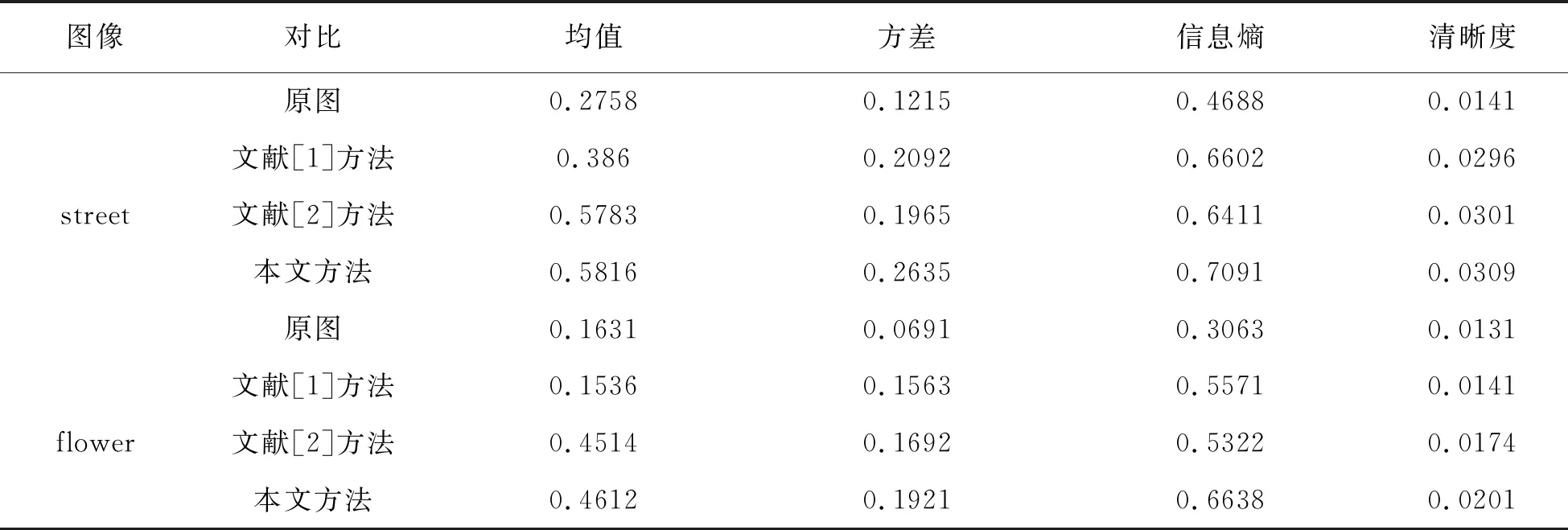
表1 三种方法图像增强性能分析

从客观评价标准可以判断出，使用本文方法对图像进行处理，其均值、方差、信息熵和清晰度都比其他两种方法实现的效果更好，准确客观地反映出本方法在图像增强处理方面更具优势.

5 结论

本文研究基于频率分解的平面图像色彩增强方法，采用该方法进行平面图像色彩增强时，从照度的估量到入射光分量和反射光分量的优化，再到HSV色彩空间的校正，都达到了较为普遍的应用性和计算的简便性效果.通过增强后的视觉观察以及客观的指标评价，都可以验证本文方法增强后的图像明暗适度，色彩饱满，细节清晰，可以广泛地应用在平面图像色彩增强方面.