多油箱飞行器飞行过程质心变化机理研究

张斌，甘屹，李炳初，杨磊，姚正宇

（200093 上海市 上海理工大学 机械工程学院）

0 引言

飞行器在飞行过程中通过若干个油箱联合供油以满足飞行时发动机的工作需求。在飞行过程中，随着各个油箱由于供油而出现的油量变化及飞行器在执行飞行任务时可能发生的姿态的变化，将使得飞行器的质心位置发生变化，进而影响到飞行器的控制。飞行器质心的变化规律对制定飞行器供油策略和控制策略尤为重要，文献[1-3]中虽然提出了针对运动容器中液体质心变化的计算方法，但对于飞行器而言，其拥有多个油箱，各个姿态下油液与油箱所形成截面形状并不一样，而且在飞行过程中，油箱的油液的量会因供油而减少，所以上述方法对飞行器质心在飞行过程的质心计算并不完全适用。本文综合现有的方法，对多油箱飞行器运行过程中的质心位置变化建立了数学模型。

1 问题背景

假设所研究飞行器共n 个油箱，飞行器的结构如油箱的位置、形状、尺寸、供油关系和供油速度等因素将影响质心变化，根据实际情况对飞行器的结构和供油限制作以下假设：

（1）油箱为长方体，固定于飞行器内部，设第i 个油箱内部长、宽、高分别为ai，bi，ci，i=1，2，…，n；油箱长、宽、高的3 个方向与飞行器坐标系的x，y，z 轴3 个方向平行；

（3）本研究只讨论飞行器俯仰时在重力作用下油箱姿态变化和油箱油量的变化引起飞行器质心的变化。

2 建模

2.1 模型假设

约定两个坐标系如下：

（1）惯性坐标系O-XYZ：飞行器不工作时，不载油飞行器质心为原点O，飞行器在地面上水平方向为纵向中心轴X 轴，以飞行器前方为正向，重力反向为Z 轴正向，以右手法则确定Y 轴。

（2）飞行器坐标系O（t）-X（t）Y（t）Z（t）：t 时刻，不载油飞行器质心位置为原点O（t），飞行器纵向中心轴为X（t）轴，以飞行器前方为正向，Y（t）轴垂直于X（t）轴所在的飞行器纵剖面，且O（t）-X（t）Y（t）组成右手坐标系，通过右手法则确定Z（t）轴。

（3）飞行器t 时刻俯仰角θ（t）：飞行器坐标系O（t）-X（t）Y（t）Z（t）中X（t）轴与惯性坐标系O-XYZ 中O-XY 水平面的夹角，X（t）轴正方向在重力方向分量与重力方向相反时θ（t）为正。

（4）t=0 时（地面上）飞行器坐标系O（t）-X（t）Y（t）Z（t）与惯性坐标系O-XYZ 重合，不考虑滚转飞行，则O（t）-X（t）Y（t）Z（t）中Y（t）正向与O-XYZ 中Y 轴正向始终保持一致。

（5）所求质心变化的坐标是相对于不载油飞行器质心O（t）的坐标。

2.2 建立模型

2.2.1 建模目标及约束条件

根据飞行器在飞行过程中n 个油箱的供油速度及飞行过程中的变化数据，计算该过程中飞行器质心坐标的变化曲线，约束条件为飞行器在执行任务中轨迹坐标及问题背景中的所有约束项。

2.2.2 油液状态分析

飞行器飞行过程中质心约束于t 时刻的θ（t）与各油箱油液体积Vi（t）。图1 是油箱ZOX 截面。ZOX 截面坐标原点相对于油箱中心的坐标为，OO1X 是飞行器飞行时与地面平行的面，∠YOO1，∠ZOO1分别表示飞行器在俯冲、仰冲时油箱YOX 面与水平面的夹角θ（t）。

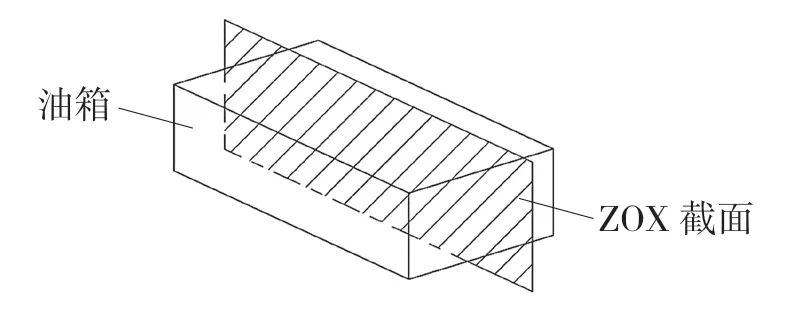
图1 油箱ZOX 截面Fig.1 ZOX cross section of fuel tank

图2 为飞行过程中油箱ZOX 截面上油液在俯、仰角两种情况下的各个状态，飞行器质心随油液ZOX 面的形状而变化。

图2 t 时刻θ（t）与油箱Vi共同影响下的油箱内油液状态Fig.2 Fuel state in the tank under the joint influence ofθ（t）and Vi at time t

2.2.3 临界条件

从图2 可知，ZOX 截面的主要状态有直角三角形、梯形及五边形。飞行器飞行过程中，在t时刻油量Vi（t）与θ（t）是确定值，此刻油液的状态是图2（a）中的某一个状态（ZOY 截面）。此处引入2 个极限量Vi1与Vi2。其中，在θ（t）的情况下，若油液恰好在OO1X 面上，此时的油液体积为Vi0；若油液恰好在BO1X 面上，则油液体积为Vi1。如图3 所示，OO1X 与BO1X 均与地面平行。

图3 油液状态Fig.3 State of fuel in tank

对于Vi1与Vi2，有以下几个说明：

（1）Vi1与Vi2的大小与油箱本身的长宽高和飞行时θ（t）有关，在θ（t）角确定的情况下，2 个极限值则固定不变；

（2）根据t 时刻油箱内剩余油量（或液面高度）与Vi1，Vi2做对比，即可得到YOZ 截面的形状，进而可求得质心坐标。

（3）图4 为各油液状态下的Vi1，Vi2，θi0表示第i 个油箱在ZOX 截面的面对角线.

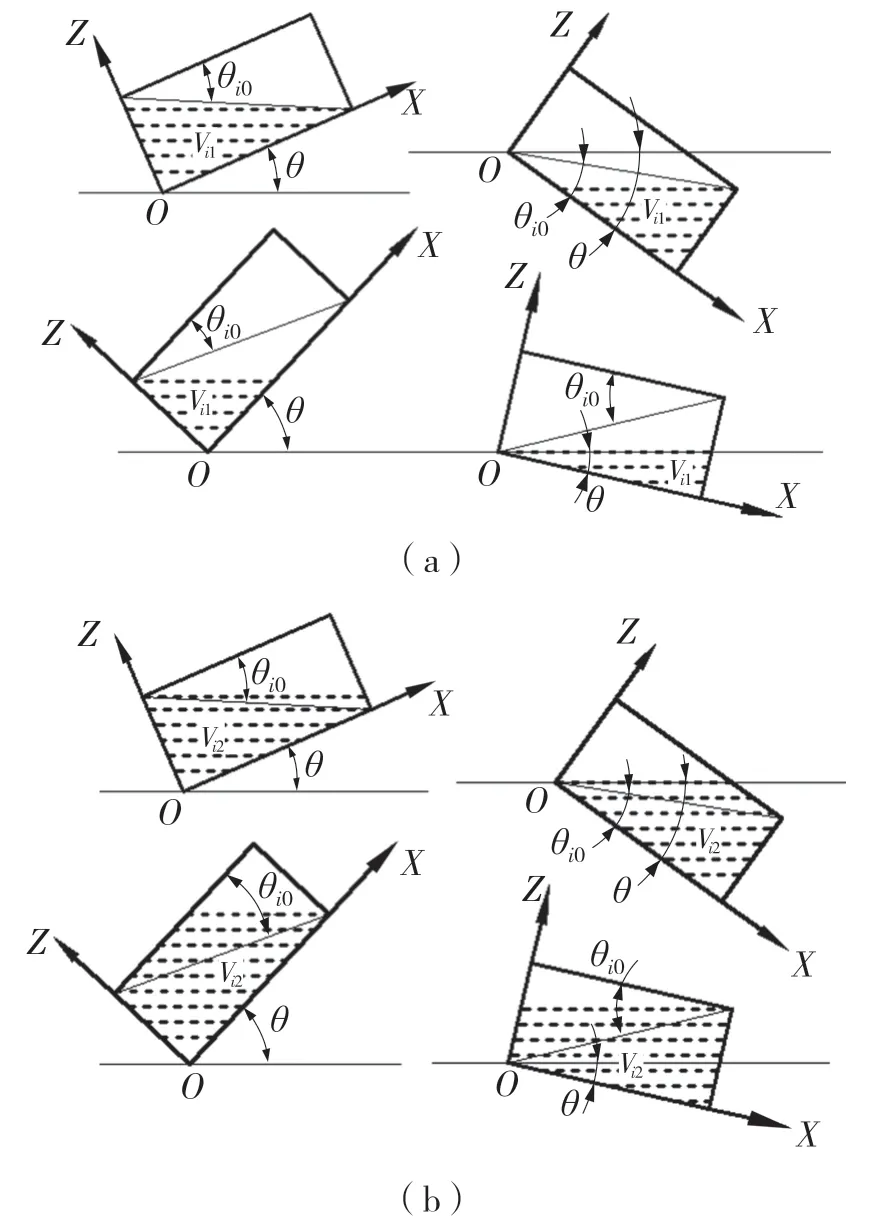
图4 油箱油液状态临界条件Fig.4 Critical condition of fuel

2.3 质心求解

2.3.1 质心

质心指物质系统上被认为质量集中于此的一个假想点。t 时刻第i 油液质心与油箱中油液的状态有关，由于各油箱均为长方体，则油液在油箱中的状态为三棱柱、四棱柱或者五棱柱，油液的密度均匀。由质心的定义可知，油液在俯仰的各个状态下的质心均在ZOX 截面上，油液在ZOX 截面的形心即为质心。由此可得，t 时刻第i 个油箱中油液的质点σi，与飞行器空载时质心0联合，即求得t 时刻飞行器的质心。

2.3.2 油液状态分类及其质心计算

根据油液在ZOX 截面的状态，可以将其划分为如图5 所示的8 种情况。其中，状态a，e，g 截面均为三角形；状态e，d，h 截面均为四边形；其余2 种情况则为五边形.

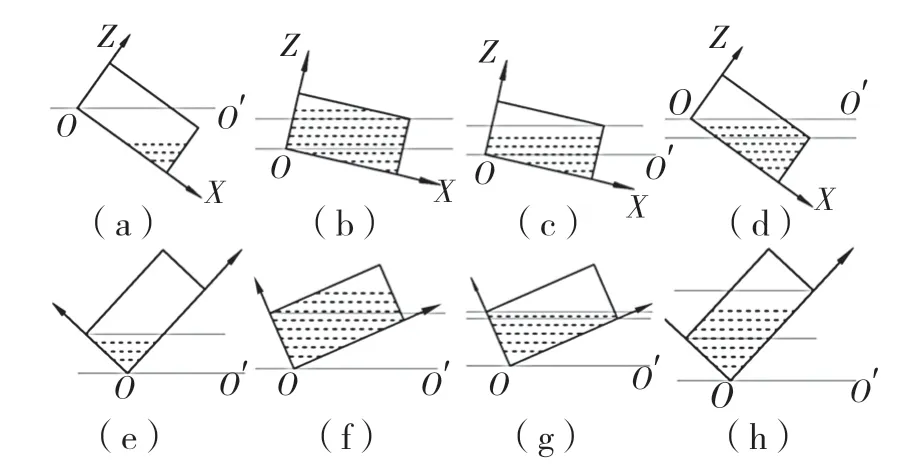
图5 临界条件下油液在ZOX 截面的多种状态Fig.5 Multiple states of fuel in ZOX section under critical conditions

不同截面的形心可通过下列方法得出，ZOX截面形心确定后，即可解得各油箱的质心[5]，质心关于油箱中心的Y 轴坐标为0。

截面为三角形的情况，若其三点坐标分别为（x1，z1），（x2，z2），（x3，z3），则其形心（xs，ys）计算公式为

平面多边形可被剖分为有限个简单图形X，X2，…，Xn，这些简单图形的质心为C1，C2，…，Cn，面积为A1，A2，…，An，则此多边形形心坐标为（x，y）

此模型为四边形时划分为一个矩形和一个三角形，求出各个点坐标，得到两个简单图形的重心坐标（x1，y1）和（x2，y2），面积为S1，S2，则此四边形的形心坐标为

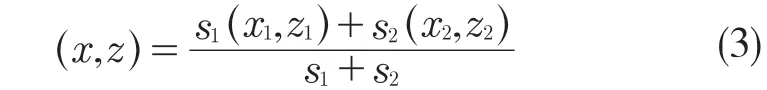
同理，五边形的形心为

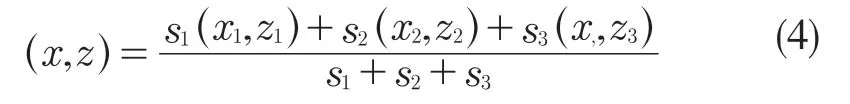
则解得n 个油箱各自相对于油箱中心的质心坐标为（xi，0，zi）abc，经过坐标转换，可得各油箱相对于飞行器原点的质心坐标为（xi，yi，zi），则油箱构成的质点系的质心坐标为

然后计算飞行器整体与油箱构成的质点系的质心坐标即为最终的质心坐标。M 为飞行器质量，Mt为油箱质点系坐标：

2.4 算法设计

2.4.1 算法流程

Step1：初始化，油箱号i=0，时间t=0，循环次数N=0，最大循环次数Nmax.各飞行器初始油量Vi（0）。

Step2：准备阶段，i=i+1，求得第i 个油箱在ZOX 截面的面对角线关于X 轴倾角。

转至step3。

Step3：根据油耗计算出t 时刻油液体积Vi（t）=Vi（t-1）-∆V，转至step4。

Step4：获取t 时刻θ（t），若θ（t）<0，则转至step5；否则转至step8。

Step5：若|θ（t）|≤θio，则转至step6，否则转至step7。

Step6：计算此状态的Vi1与Vi2，计算式分别为

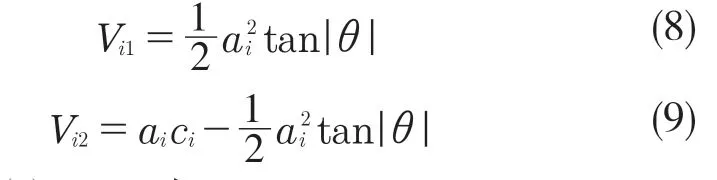
比较Vi（t），Vi1与Vi2：

若Vi2≤Vi（t）≤Vim，则为状态b，转至step12；

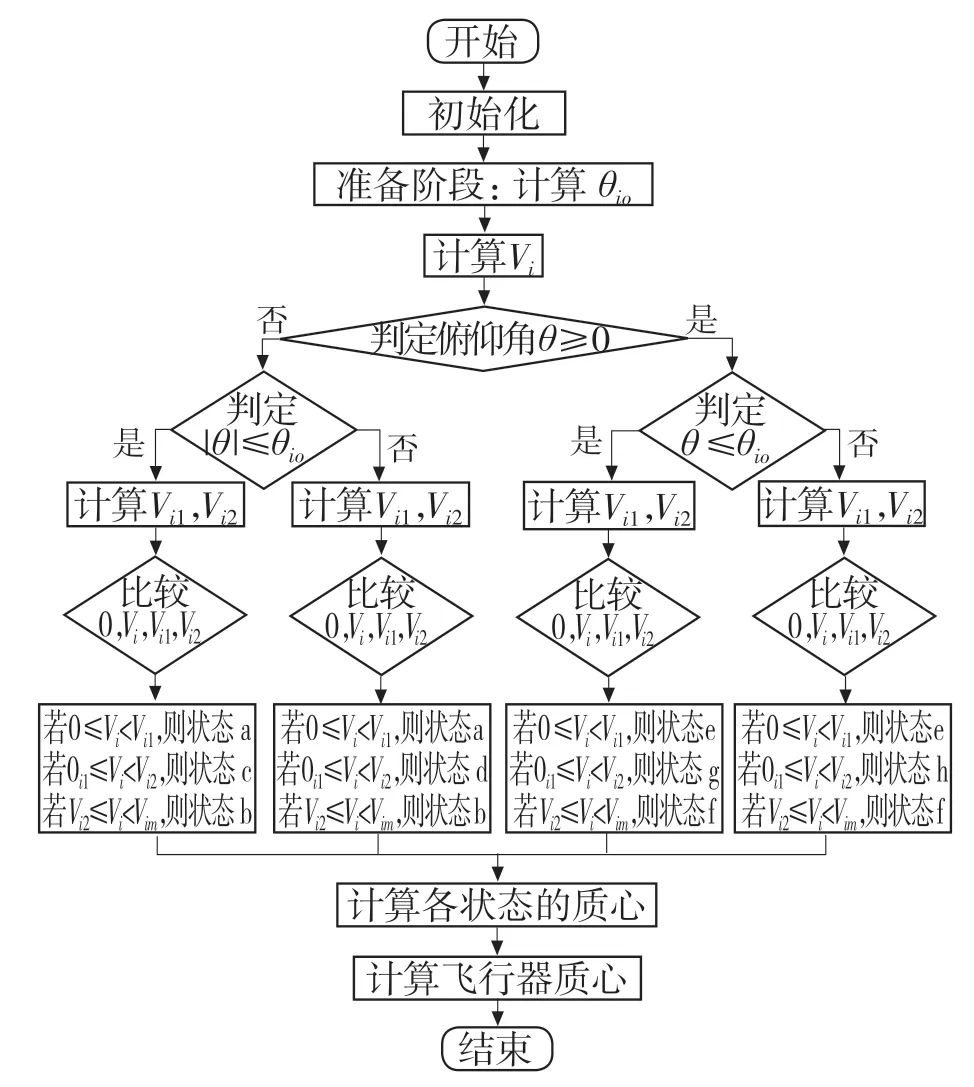
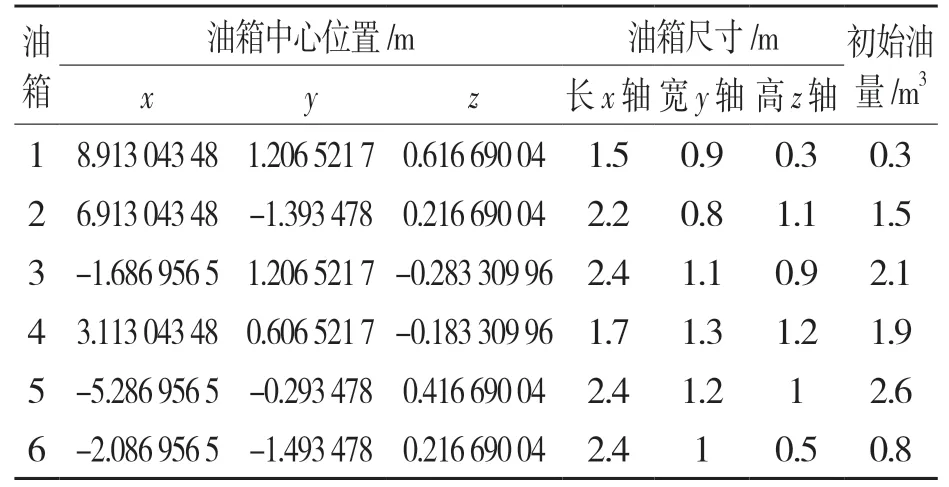
若Vi1≤Vi（t）

若0≤Vi（t）

否则终止。

Step7：计算此状态的Vi1与Vi2，计算式分别为

比较Vi（t），Vi1与Vi2：

若Vi2≤Vi（t）≤Vim，则为状态b，转至step12；

若Vi1≤Vi（t）

若0≤Vi（t）

否则终止。

Step8：若|θ（t）|≤θio，则转至step9；否则转至step10；

Step9：根据式（8）与式（9）计算此状态的Vi1与Vi2，比较Vi（t）、Vi1与Vi2：

若Vi2≤Vi（t）≤Vim，则为状态f，转至step12；

若Vi1≤Vi（t）

若0≤Vi（t）

否则终止。

Step10：根据式（10）与式（11）计算此状态的Vi1与Vi2，比较Vi（t），Vi1与Vi2：

若Vi2≤Vi（t）≤Vim，则为状态f，转至step12；

若Vi1≤Vi（t）

若0≤Vi（t）

否则终止。

Step11：油液在ZOX 截面为三角形，根据式（1）计算形心后转换为油液截面质心，转至step13。

Step12：油液在ZOX 截面为多边形，根据式式（3）、式（4）计算形心后转换为油液质心，转至step13。

Step13：将i 油箱油液质心坐标保存，若i

Step14：根据式（5）、式（6）计算飞行器空载油的质心与式n 个油箱质点系在t 时刻质心，并保存，转至step15。

Step15：t=t+1，N=N+1,若N ≤Nmax，转 至step1；否则转至step16。

Step16：算法终止。

上述算法的流程如图6 所示。

图6 算法流程图Fig.6 Algorithm flow chart

3 实例分析

3.1 实例数据

表1 为某飞行器6 个油箱的形状及相对于飞行器坐标的位置信息及初始油量。

表1 飞行器油箱形位尺寸及其他数据Tab.1 Aircraft tank shape and size and other data

飞行器俯仰角变化及各油箱供油速度数据选用2020 年“华为杯”第17 届研究生数学建模竞赛F 题附件2 中数据，飞行器各时间俯仰角变化如图7 所示，各油箱供油时间段及供油速度如图8 所示。

图7 飞行器俯仰角度Fig.7 Pitch angle of aircraft

图8 各油箱供油速度Fig.8 Delivery rate of each fuel tank

3.2 计算结果

根据算法流程编辑程序,执行源代码后所得质心变化曲线如图9 所示。

图9 质心变化曲线Fig.9 Curve of centroid change

由计算结果可知，质心在各个坐标轴上均发生了连续的变化，以质心X(t)轴方向的坐标变化较大，其主要原因是相对于油量的变化，俯仰角对质心的影响最大。结合图7 所示，在5 000 s 附近，俯仰角逐渐趋于零，而质心的X(t)坐标也亦在此时间段快速趋于零。Y(t)坐标的变动较为平缓，主要原因是：当飞行器俯仰飞行时，各油箱的质心坐标变化主要在ZOX 截面上，其在Y轴方向并未有变化，引起此刻飞行器Y(t)坐标变化的原因主要是各油箱油量的变化。相对于飞行器俯仰飞行而言，各油箱油量变化带来的质心较小。质心Z(t)轴方向的坐标亦受俯仰角与油量的影响。在此实例中，其变化亦平缓，而其变化的趋势与俯仰角变化的趋势相似，先上升后下降，但变化的幅度小于X(t)轴方向坐标的变化幅度，其原因是其受油量变化的影响.

以上实例可知，计算模型可有效地计算多油箱飞行器在飞行过程中的质心变化曲线。

4 结论

本文综合现有方法解决了多油箱飞行器在俯冲或仰冲时质心变化的问题，经实例验证，数学模型可有效得出飞行器飞行过程中质心的变化曲线，且符合定性分析的趋势，在获知各油箱供油速度、油箱形状尺寸及俯仰角的情况下应用算法模型可有效地解决此类问题，且具备相应的实用性。

研究中对油箱形状、坐标、运行轨迹等方面进行了简化，大大减小了运算难度，在实际情况下，飞行器的飞行及油箱供油的过程则比较复杂；再者，计算模型只考虑了飞行器在俯仰状态下的质心变化，对更复杂的状态如偏航和滚转并未考虑，有待进一步探索。