振镜系统自适应离散滑模控制器设计与仿真

王云龙，陈光胜

（200093 上海市 上海理工大学 机械工程学院）

0 引言

当前，国外振镜系统生产厂家主要有SCANLAB 公司、GSI 公司、CTI 公司等，其中SCANLAB 公司的振镜扫描系统达到行业最高质量标准；国内主要生产厂家有深圳大族思特科技有限公司、上海眸特电机科技有限公司、北京金海创科技有限公司等。国内振镜行业起步较晚，技术相对国外较为落后，但随着近些年的发展也具有一定的实力。

控制算法是影响振镜控制系统性能的核心因素。当前在振镜控制系统中的控制策略应用主要以PID 算法为主。马玉中[1]采用数字PID 控制激光振镜扫描系统，在大角度定位时，系统响应较慢；井锋[2]提出了一种改进的模糊PID 算法，但模糊规则在数字电路的实现较为复杂。由于PID控制算法及其改进算法在实际应用中的限制，将高性能的控制算法引入到振镜控制系统中就变得尤为迫切[3]。

本文基于现代控制理论，并结合计算机技术，研究了一种基于自适应离散滑模变结构的振镜系统控制器设计原理与方法，利用离散滑模变结构控制系统的准滑动模态[4]具有一定的不变性来增强系统的鲁棒性，并通过自适应控制在线调整趋近律中的控制增益，提高系统动态品质。

1 振镜电机数学模型的建立

振镜电机是一种特殊的摆动电机，其基本原理是通电线圈在磁场中产生力矩，但只能偏转一定角度，偏转角度与电流成正比。

振镜的电枢平衡方程为

式中：R——振镜电机的电枢电阻；L——振镜电机的电枢电感；Eb——振镜电机的反电动势；i——振镜电机的电流。

振镜电机的转矩平衡方程为

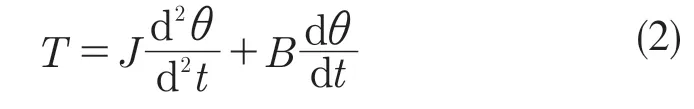
式中：T——振镜电机的线圈电流产生的电磁转矩；J——振镜电机转子的转动惯量；θ——振镜电机转子偏转角度；B——振镜电机内部的粘性阻尼系数。

振镜电机的电磁转矩方程为

式中：Kt——振镜电机的转矩系数。

振镜电机的反电动势为

式中：Kb——振镜电机的反电动势系数。

将式（1）—式（4）分别进行拉普拉斯变换，经整理简化后，得到振镜电机伺服系统的传递函数为

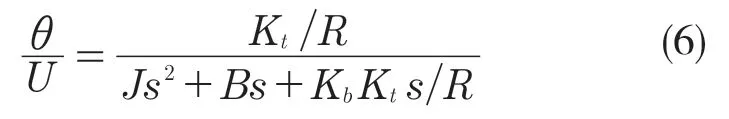
虽然电机中实际存在反向电动势，但在放大器中有一个电流调节环路可以补偿反向电动势造成的转矩损失，因此可以在模型中忽略其影响[5]。式（6）可以简化为

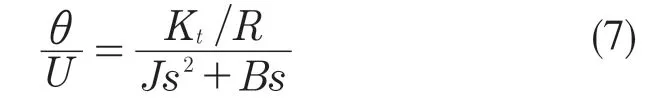
因此，得到振镜电机控制系统动力学模型，如图1 所示。

图1 振镜电机控制系统动力学模型Fig.1 Dynamic model of galvanometer motor control system

图1 中：u——控制信号；Ka——电流放大系数；i——电流；Td——摩擦力矩；ω——转子角速度；θ——转子角位置。

由图1 得振镜电机控制系统的状态空间表达式为

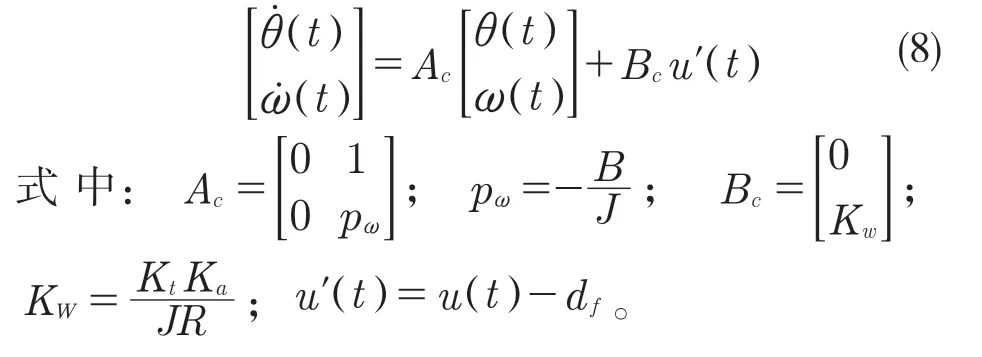
振镜电机实际运动中，可忽略非线性摩擦的影响，只考虑库伦摩擦力Tfc，则摩擦力的等效输入

对式（8）进行零阶保持离散化，得系统离散状态空间表达式为

2 自适应离散滑模控制器设计

振镜系统的控制实际上是跟踪问题，设R(k)为希望的指令信号，xe(k)=e(k)=R(k)-x(k)。则振镜系统式（9）的离散状态方程为

2.1 离散自适应趋近率

对于离散系统，滑模变结构控制不能产生理想的滑动模态，只能产生准滑动模控制[4]，其指数趋近率为

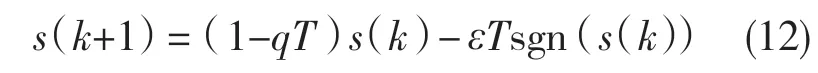
式中：ε>0；q>0；1-qT>0；T——采样周期。

参数ε是一个关键参数，ε值越小，可以降低系统抖振，但过小的值会导致系统到达切换面的趋近速度过慢，考虑到技术、设备等实际因素，采样周期也不可能取特别小，因此理想的ε值应该是时变的[6-7]。由s（k）递减得到充分条件为

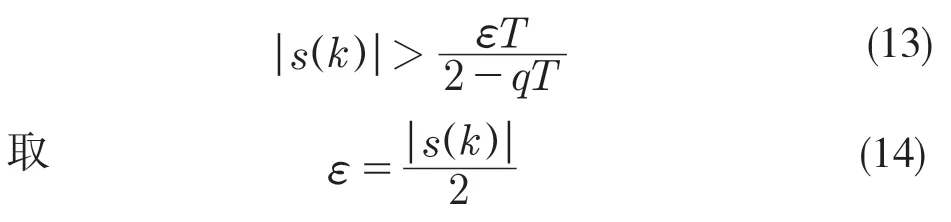
将式（14）代入式（12），得到自适应离散趋近率为

结合式（9）、式（11）、式（15），假设CB ≠0，则振镜系统位置跟踪的控制率为

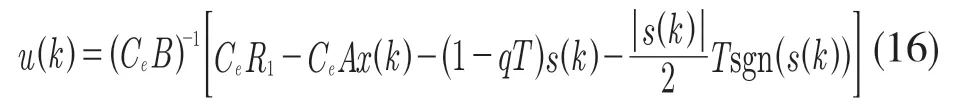
式中：s（k）=Cex（k）；Ce=[c，1]；c，q——影响滑模控制的两个重要参数，适当的取值可以得到良好的系统性能；R1=[r（k+1），dr（k+1）]，可以通过外推法得到。

2.2 系统稳定性验证

离散系统到达条件为

选取李雅普诺夫函数

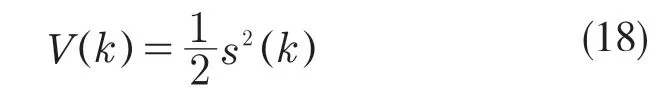
根据李雅普诺夫定理，满足s(k)=0 是全局渐近稳定平衡面的到达条件可取为

当采样时间很小时，离散滑模的存在和到达性条件为[8]

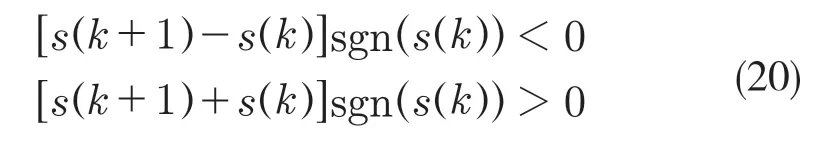
由自适应离散趋近率式（15）可得

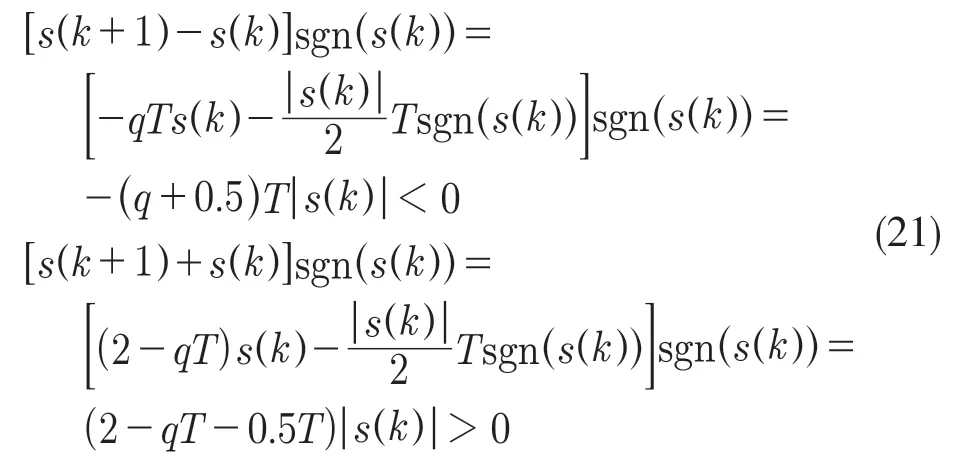
因此，改进后的趋近率满足滑动模态的存在性和到达性条件，控制系统是稳定的。

3 参数辨识

根据式（9）、式（15）、式（16），需要处理的参数有J，Kt，Ka，R，B，Ts，df，c，q，其中Kt，Ka，R 可通过测量和计算得到，Ts根据现有硬件条件取Ts=2.5×10-5(s)，根据调试经验取 x=6 000，q=8 000。

依据改进的最小二乘法对J，B，df进行离线辨识[9]，得到仿真模型的参数见表1。

表1 仿真模型的参数表Tab.1 Parameters of simulation model

4 仿真与实验

本文所选振镜电机系统的性能指标见表2。

表2 振镜系统性能指标表Tab.2 Performance indicators of galvanometer system

根据式（11）、式（16）、表1，在MATLAB中建立相应振镜系统控制模型并进行仿真实验，结果如图2、图3 所示。

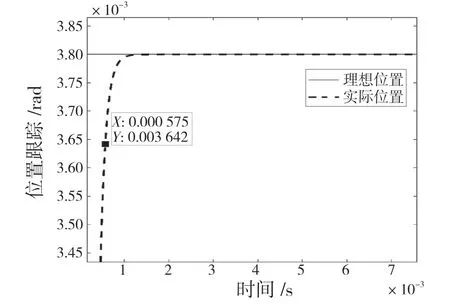
图2 1%全行程阶跃响应Fig.2 1% full stroke step response

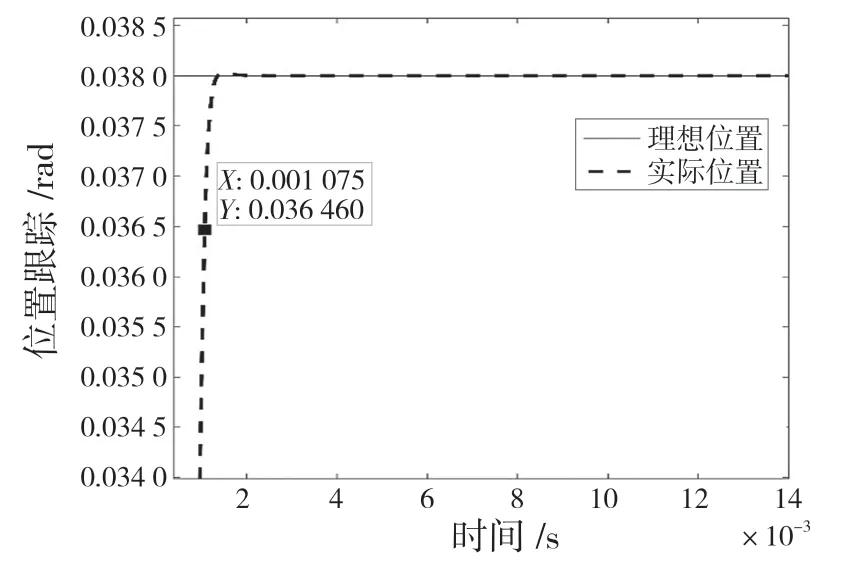
图3 10%全行程阶跃响应Fig.3 10% full stroke step response

如图2、图3 所示，当振镜系统输入为1%全行程时，阶跃响应为575 us（按阶跃响应95%标准）,小于指标值800 us，超调量小于3%；当振镜系统输入为10%全行程时，阶跃响应1.075 ms（按阶跃响应95% 标准）,小于指标值2.5 ms,说明本文所设计的离散自适应滑模控制器满足振镜系统的性能指标。

如图4所示，控制器增益值在起始阶段较大，这一阶段系统快速趋近至滑模面，到达滑模面后，增益值减小，有助于减小系统抖振。对比图5 和图6 滑模控制器的相轨迹图可知，所设计的自适应增益使得系统相轨迹在滑模面上的运动更加平滑，动态品质有明显提高。

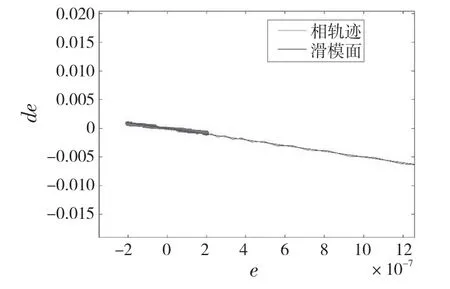
图5 常量增益值系统相轨迹图Fig.5 Constant gain value system phase trajectory

图6 自适应增益值系统相轨迹Fig.6 Adaptive gain value system phase trajectory

振镜电机在实际工作时，位置曲线近似为三角函数（单一或组合）曲线，本文选取最简单的正弦曲线作为输入参考信号。如图7 所示，振镜系统在跟踪正弦信号方面有良好的表现，说明本文设计的离散滑模控制器性能稳定可靠。

图7 正弦信号位置跟踪Fig.7 Sinusoidal signal position tracking

5 结语

本文针对离散振镜系统提出了一种自适应离散滑模控制方法并验证了系统稳定性。通过在线调节控制器自适应增益，可使系统较快趋近滑模面，同时减少抖振，提高系统的运动品质。参数辨识得到振镜系统的相关参数并结合仿真模型进行实验，有效地验证了控制方法的动态和稳态性能，能够满足振镜系统在实际应用中的性能。基于趋近率的离散滑模控制器结构简单易实现，自适应增益有利于系统动态性能的提升。