基于改进SAFL 法的曲轴疲劳实验失效数据统计分析方法研究

陈钰庭，唐嘉豪，孙嵩松

（210037 江苏省 南京市 南京林业大学 汽车与交通工程学院）

0 引言

随着我国经济的快速发展以及生活水平的提升，汽车已经逐渐成为目前国内数量最多、最普及、活动范围最广、运输量最大的现代化交通工具，也是与人类社会的发展最息息相关的交通工具[1-5]。作为汽车的“心脏”部位，发动机零部件可靠性的优劣，直接影响着汽车的正常运行与否。在目前的实际工程中，曲轴等大型汽车零部件的疲劳特性主要是通过疲劳试验法获取，该类方法往往通过对零部件在不同载荷水平下的疲劳寿命进行统计分析，从而获得零部件在给定服役寿命要求下的疲劳强度分布特性。基于SAFL 法处理疲劳试验数据已经得到了广泛应用，高镇同[6-7]等详细论述了疲劳试验的基本概念、定义和公式；周迅[8-9]、李舜酷[10]论述了曲轴疲劳试验方法的原理、特点并介绍失效数据的处理[8-10]；陈晓平[11]等利用极大似然法测定曲轴疲劳性能。但是应用该方法在对大型零部件进行疲劳试验时，由于传统的QCI 通常由材料自身的抗拉强度和断面收缩率计算获取，而对于绝大多数零部件，这两个参数都会因为尺寸结构、表面处理工艺等因素产生变化，因此直接采用材料的参数来计算零部件的QCI 点存在一定的不合理性。

针对上述不足，已有学者对传统的零部件SAFL 疲劳试验方法进行改进，提出一种新的疲劳试验数据统计分析方法[12]，对曲轴等零部件的疲劳试验数据进行分析，获得其在给定疲劳极限下的强度。本文基于改进的SALF 法，进行了疲劳试验在N0=107疲劳寿命下疲劳极限的正态分布、对数正态分布、威布尔分布3 种分布形式下曲轴疲劳失效数据的分析，得到更符合工程实际的统计结果。对比研究结果表明，相对于正态分布以及对数正态分布模型，采用三参数的威布尔分布得到的强度分布结果更符合工程实际的需求，具有更广泛的实用价值。

1 曲轴疲劳极限分析

传统工程应用中一般利用疲劳极限统计分析法（SAFL-Statistical Analysis for Fatigue Limit）对曲轴的疲劳试验数据进行拟合，该方法的理论基础为：将试件所受载荷及在此载荷下的寿命绘制在双对数坐标之中，两者呈线性关系，且在存在一个符合这一lgS-lgN 线性关系的1/4 次循环断裂点A（即QCI 点）[13]，原理如图1 所示。

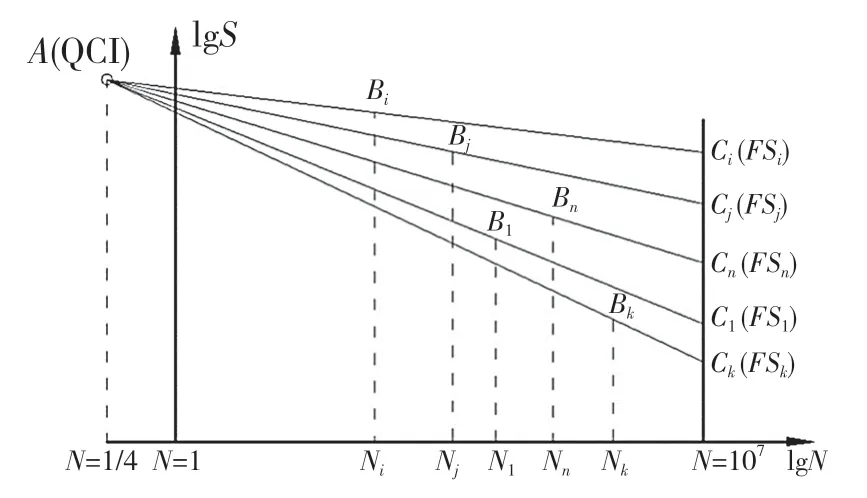
图1 应力-寿命在双对数坐标上的关系Fig.1 Relation between stress and life in couple log coordinate

如图1 所示，设第i 号试件在载荷Si的作用下试验至Ni次时发生断裂，将这一点表示在lgS-lgN 坐标上为Bi点，连接QCI 点与Bi点，并延长至给定寿命的垂线N=N0（N0=107），交于Ci点，该点的纵坐标为用第i 个试件测得的母体疲劳极限估计值FSi，可由式（1）、式（2）确定：

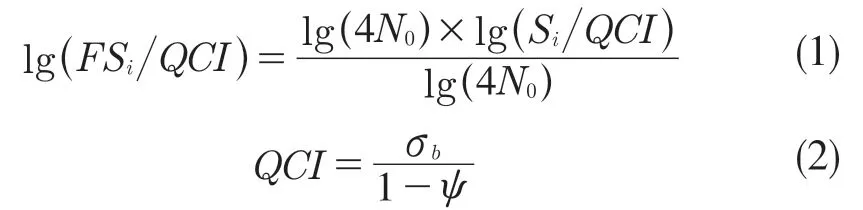
式中：σb——抗拉极限；ψ——断面收缩率。

实际工程中获得抗拉极限和断面收缩率这两个参数的方式一般是通过对所选材料的标准试棒进行拉伸试验获得，但对于曲轴而言，其拉极限和断面收缩率会随着表面热处理等加工工艺而发生变化，整体硬度和脆性都增大，导致使用标准试棒测得的实验数据来计算曲轴QCI 点的应力值时发生偏差，使得结果具有不合理性，因此采用上述方法对某曲轴试验数据进行分析时发现，试验得到的QCI 点的疲劳寿命数值远远小于理论QCI 对应的寿命值。针对这一不足，一些研究者提出了一种改进后的SAFL 法[12]。该方法主要分为两步：（1）采用最小二乘法对已有的疲劳试验数据进行拟合，以找出试件应力值与寿命之间的对数线性关系；（2）根据拟合所得到的线性关系，选取某一低周疲劳寿命作为测定数据标出QCI 点，将QCI 点依次连接试验点并延长至该垂线，得到若干交点，取其纵坐标得到高周疲劳区曲轴应力分布情况。计算公式为

式中：FSi，Ni，Si——用第i 个试件，测得的母体疲劳极限的一个估计值、载荷及疲劳寿命；SA——QCI 点的应力值；NA——该应力下构件的疲劳寿命值。

2 不同分布方法对比研究

基于改进的SALF 法[12]，借由参考文献[13]提供的曲轴疲劳寿命实验数据，可以得到在N0=107下的疲劳极限。接着，对其进行正态分布、对数正态分布、威布尔分布这几种形式下曲轴疲劳失效数据的分析。

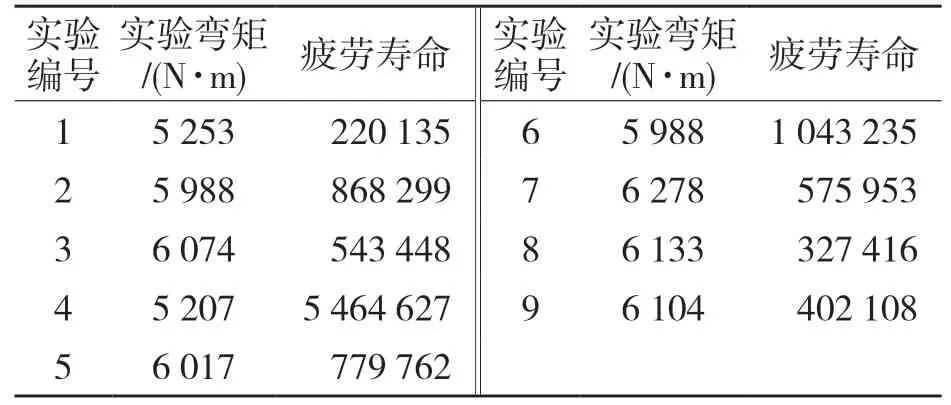
表1 某曲轴疲劳寿命Tab.1 Fatigue limit of crankshaft

2.1 正态分布模型的统计回归

在正态分布模型中，要将问题化为线性回归问题，对试验数据做如下变换：

用变换后的xi和yi进行最小方差拟合，得线性方程式

接着可以得到正态分布的均值和方差的估计值分别为

2.2 对数正态分布模型的统计回归

与正态分布的转化方式类似，对数正态分布的统计回归首先要将疲劳极限的估计值取对数，再将问题化为线性回归问题

对所得xi和yi拟合，得到线性方程(6)，进而特征参数的估计值分别为

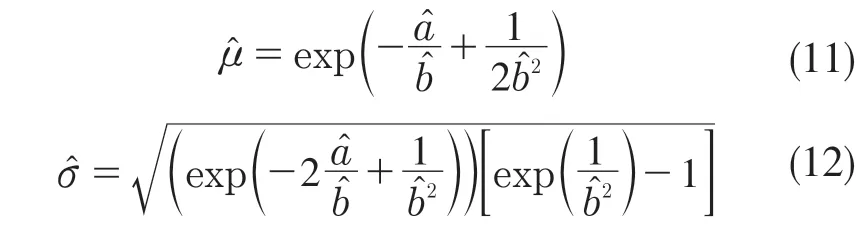
2.3 威布尔分布模型的统计回归

三参数威布尔分布的函数表达为

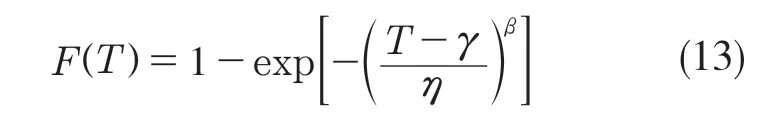
由式（13）可以看出，威布尔分布需要对3个参数，即尺度参数η，形状参数β和位置参数γ进行估计，属于非线性的曲线回归问题。对于这种情况，可以应用搜索寻优的方法来计算γ的值，通过迭代法求解参数的估计值，在单次迭代中，问题就转化为线性回归问题。设在第1 次迭代中，位置参数的取值为

对试验数据进行线性化转换为

迭代计算的实质是获得一个合适的γ估计值以实现对线性方程的最佳回归。经过比较后发现，采用单形调优法（Nelder-Mead Method)得到的γ值效果更加理想，它可以用很短的计算时间获得高精度的估计值。

在迭代结束之后，γ的估计值直接得到，根据最后一次迭代中的线性回归结果，分别有

均值和方差分别为

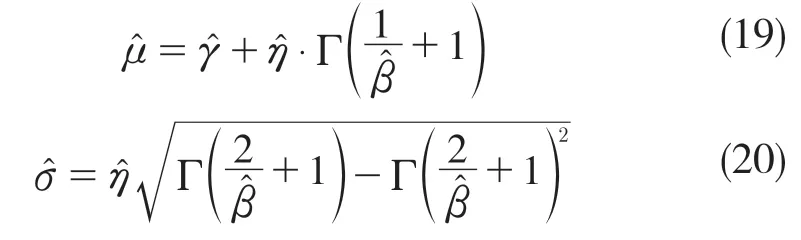
式中：Г——伽玛分布函数。

3 实际数据分析

表2 为曲轴弯曲疲劳试验极限弯矩分别在正态分布、对数正态分布、威布尔分布下的统计回归结果。对比3 种分布模型，从统计回归的相关性上看，3 种分布方式都可以满足误差小于5%的精度要求。但从概率分布的合理性来看，正态分布和对数正态分布在载荷为零时失效概率都不为零，这显然是与实际情况不相符的。而威布尔分布相比于前两者能够得出相对合理的零失效概率的疲劳极限点，更好地描述曲轴失效概率的分布情况。因此，综合上述对比情况来看，用威布尔分布作为曲轴的疲劳失效数据的分析模型较正态分布和对数正态分布更为合理。

表2 3 种分布模型的统计回归结果Tab.2 Statistical regression results of three distribution models

4 结论

本文基于改进的SAFL 法，得到对某曲轴给定寿命下的疲劳极限，并进行正态分布、对数正态分布、威布尔分布3 种形式下曲轴疲劳失效数据的分析。结果表明，以威布尔分布作为处理曲轴疲劳寿命模型，其在统计的相关性和0 失效概率上都是相对合理的。