锂离子电池极耳分布对电极应力的影响
马德正,李培超
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
锂离子电池是一种新型高效绿色的可再充电电池,因具有能量密度高、工作电压高、自放电率低、无记忆效应的优点被广泛应用[1-2]。在电池充放电过程中,锂离子嵌入/脱出以及温度的变化将会导致电极内部产生应力,应力过大将导致电极活性材料剥落、解体和SEI 膜的增加[3-5],进而导致电池循环寿命下降和容量的损失[6-7]。温度对电池安全性和循环寿命的影响至关重要,因此电池结构优化设计及其热管理极为关键[8]。
电池极耳在电池内部主要起到连接集流器的作用,很多学者对极耳结构进行了分析研究。陈宏[9]等通过实验方法研究了高速放电条件下,不同极耳位置分布和几何尺寸对电池的影响,并最终对其尺寸提出优化;莫治波[10]等对圆柱形锂离子电池极耳位置进行了研究,发现将极耳由侧边改到中间能有效降低电池内阻;王安安[11]等通过数值模拟研究了电池极耳在双侧分布和单侧分布下对软包电池的电芯热行为的影响;龙梅和唐有根[12]通过对不同尺寸和位置分布的极耳进行实验研究,发现极耳宽度和厚度越大越有益于电池的高速率放电;陈才星[8]等建立了锂离子电池的三维分层结构模型,分析了电池温度场的分布特征,同时对极耳尺寸进行了优化,降低了电池放电产热;黄伟国[13]等通过对铅炭电池的极耳在同侧和对侧排布方式下的充电析氢量、放电曲线和电池容量的实验研究,发现极耳在对侧布置下电池放电电压和循环寿命会更高。以上工作皆在分析极耳排布对电池电化学和热性能的影响,但均未考虑电极极耳对电极应力的影响。
本文建立了一个三维锂离子电池电化学-热-力耦合模型对电极内部电流场、温度场和应力场进行求解,分析相同放电倍率时正负极耳在不同排布方式下对电极应力的影响,同时对极耳尺寸和材料属性(杨氏模量和泊松比)进行了参数分析,研究其对电池内部电极应力的影响。
1 数学模型
模型选取容量为90 A·h的磷酸铁锂/石墨电池内部最小单元为研究对象,如图1 所示。图1(b)中从左至右依次为负极集流器(Cu)、负极材料、隔膜、正极材料和正极集流器(Al)。其中,电池宽度Wcell=12.69 cm,高度Hcell=19.42 cm。负极集流器厚度Lcu=3 μm,负极厚度Lneg=63 μm,隔膜厚度Lsep=16 μm,正极厚度Lpos=86.5 μm。正极集流器厚度LAl=7.5 μm;正极极耳宽Wpos=9.55 cm,高度Hpos=1.5 cm,中心与电池中心距离dpos=0。负极极耳宽度Wneg=4.55 cm,高度Hneg=1.5 cm,中心与电池中心距离dneg=3.175 cm。单元厚度Lcell=0.176 mm。

图1 模型原理图Fig.1 Schematic diagram of the model
1.1 控制方程
(1)电荷守恒
电池内部电荷守恒包含电子电荷守恒与离子电荷守恒。电极活性材料与集流器内的电子电荷守恒遵循欧姆定律,如式(1)所示。

电解液内部离子电荷守恒方程,如式(2)所示。

(2)质量守恒
电极活性材料球型颗粒内锂的质量守恒遵循菲克第二定律,如式(3)所示。
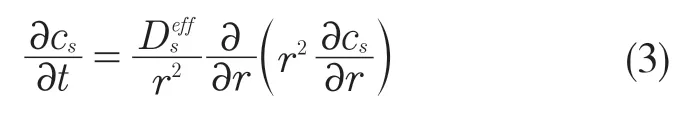
式中:cs——锂浓度;——有效扩散系数;r ——颗粒内径向坐标。
锂离子在电解液中的传递遵循质量守恒定律,如式(4)所示。

(3)电化学动力学
电极活性材料表面局部电流密度由Bulter-Volmer 方程计算得到,如式(5)所示。

式中:αa,αc——阳极和阴极的传递系数;i0——交换电流密度,如式(6)所示。
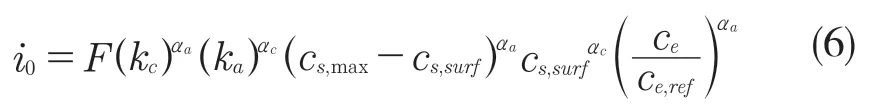
式中:ka——阳极反应速率常数;kc——阴极反应速率常数;cs,max——活性材料最大锂浓度;cs,surf——活性材料颗粒表面锂浓度;ce,ref=1 mol/m3电解液参考浓度。
式(5)中过电位η公式如式(7)所示。

式中:Eeq——电极开路电势,其值由参考温度Tref=298.15 K 下的参考电势Eeq,ref和平衡电位温度倒数dEeq/dT 计算得到,如式(8)所示。

Eeq,ref和dEeq/dT 随充电状态(SOC)的变化曲线[8]分别如图2(a)和图2(b)所示。

图2 电极平衡电位和熵变Fig.2 Electrode equilibrium potential and entropy change
(4)能量守恒
考虑电极、电解液和集流器内部产热,模型内部能量守恒控制方程如式(9)所示。

式中:ρ——密度;CP——比热容;KT——热导率。等式右侧分别表示可逆熵热、极化热、电子欧姆热和离子欧姆热。本文中不考虑电池模型同环境间的热交换。
(5)体积应变
电极活性材料内部总应变εij由机械应变、热应变=βΔTδij和扩散诱导应变=ΩΔcδij/3共同决定,如式(10)所示。

式中:β——热膨胀系数;Ω——粒子摩尔体积。
2 模型参数和验证

表1 模型参数Tab.1 Model parameters

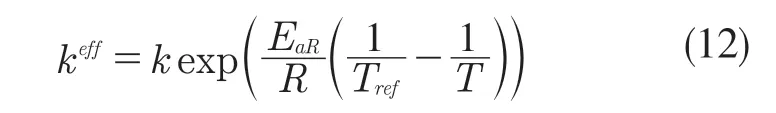
式中:Ead,EaR——扩散活化能和反应活化能。

图3(a)和图3(b)分别为数值求解到的电池电压和温度随时间变化的结果与实验数据的对比。由图可知,本文结果与实验结果相接近,从而验证了本文所建立模型的可靠性。
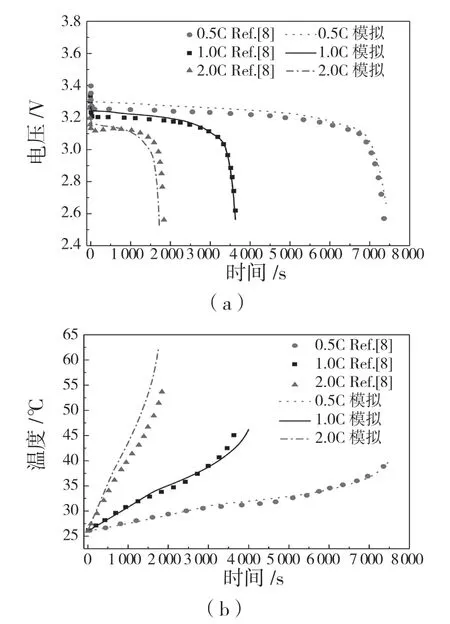
图3 电压和温度曲线与实验数据[8]对比Fig.3 Comparison of voltage and temperature curves with experimental data[8]
3 结果和讨论
3.1 极耳分布影响
为分析极耳位置分布对电池性能的影响,特将正极耳设置为与负极耳相同的尺寸。本文分别考虑A,B,C,D,E,F 六种极耳分布方式,如图4 所示。通过使用数值软件求解得到电极内部锂离子浓度和温度的分布。正极活性材料表面在1C 放电条件下放电至t=3 000 s 时的锂浓度和温度分布分别如图5、图6 所示。

图4 极耳排布方式Fig.4 Arrangement of the tab
由图5、图6 可知,正极材料在靠近负极耳侧反应更强,靠近负极耳的区域相比其它区域温度更高、锂离子嵌入量也更多;靠近正极耳区域处的反应稍弱,相比靠近负极耳区域的锂浓度和温度也略低。同时,发现靠近极耳侧的电极区域电化学反应更强。当t=3 000 s 极耳处于A,B,C,D,E,F 位置时,正极电极表面最大浓度差分别为333.5,195.2,189.3,199.9,158.8,171.1 mol/m3,正极电极表面温度差分别为0.439,0.177,0.171,0.184,0.103,0.114 K。结果发现,极耳采取对侧分布可使电池内部电化学反应更均匀。在对侧排布中,正负极耳均处于中间位置时,正极表面浓度差和温度差更小,即极耳在这种分布状态下电池电化学反应更均匀且产生热更低。

图5 正极表面浓度分布Fig.5 Surface concentration distribution of the cathode

图6 正极表面温度分布Fig.6 Surface temperature distribution of the cathode
图7 为1C 放电条件下放电至t=3 000 s 时正极活性材料表面von Mises 应力分布。由图7 可知,von Mises 应力最大值在极耳同侧排布时的最大,当极耳处于对侧排布时von Mises 最大值会降低。同时,当负极极耳位于中间位置时,即在E 和F排布方式下von Mises 最大值较小。6 种极耳分布下,von Mises 应力差值分别为1.909,1.323 8,1.113,1.217 9,0.985 5,1.081 6 MPa,极耳在E排布下正极表面von Mises 应力差值更小。当极耳在E 排布下以2C 放电速率放电至t=1 500 s 时正极表面von Mises 应力分布如图8 所示,可知当放电速率增加时正极表面von Mises应力将增大。

图7 正极表面von Mises 分布Fig.7 Surface von Mises stress distribution of the cathode

图8 正极表面von Mises 分布Fig.8 Surface von Mises stress distribution of the cathode
3.2 极耳尺寸影响
以极耳在E 方式排布为例,分析极耳的存在对正极电极表面应力的影响。图9(a)、图9(b)分别表示极耳Hpos=0 和Hpos=1.5 cm 时正极表面von Mises 应力分布。对比可知,极耳的存在会导致电极表面的最大von Mises 应力增加,且最大von Mises 应力将出现在靠近正极极耳区域。这是由于此处电极活性材料在锂离子嵌入和温度变化所导致的体积应变受到极耳的限制,进而造成在靠近极耳区域存在比较大的von Mises 应力。图9(b)—图9(d)为正极耳宽度对正极电极表面应力的影响,图9(b)—图9(d)对应的极耳宽度分别为Wpos,1.5Wpos,2.5Wpos。结果发现,极耳宽度的增加会导致电极表面应力的增大。

图9 极耳尺寸对电极应力影响Fig.9 Effect of tab size on electrode stress
3.3 极耳材料属性的影响
图10 为正极表面在不同杨氏模量和泊松比下的von Mises 应力分布,其中,图10(a)对应,E=70 GPa,v=0.34;图10(b)对应 E=20 GPa,v=0.34;图10(c)对应E=20 GPa,v=0.20。由图可知,随着正极极耳杨氏模量的降低,极耳对正极材料的变形限制作用减弱,从而电极表面最大von Mises 应力值降低。随着极耳材料泊松比的减小,正极材料表面最大von Mises 应力值将会增加,因此极耳材料应尽可能选用杨氏模量低且泊松比较大的材料。

图10 杨氏模量和泊松比对电极应力影响Fig.10 Effect of Young's modulus and Poisson's ratio on electrode stress
4 结论
本文建立了锂离子电池三维电化学-热-力耦合模型,通过与实验数据的对比验证了模型的可靠性,并通过该模型对极耳分布、尺寸和材料属性进行分析。结果如下:
(1)通过对正负极耳在6 种排布方式下的数值计算结果可知,当正负极耳处于中间位置(E排布)时电极电化学反应会更均匀,电极内锂浓度会更加均匀的同时产热会更低。负极耳居中放置能有效降低电极表面最大von Mises 应力值。
(2)对极耳尺寸的分析可知,极耳结构的存在会导致正极电极表面最大von Mises 应力从靠近负极耳的区域转移动到靠近正极耳的区域,且电极表面的最大von Mises 应力值将增大。同时当极耳宽度增加时也会导致电极表面的最大von Mises 应力值的增加。
(3)极耳结构有效杨氏模量的减小可使电极表面最大von Mises 应力值降低,泊松比的减小会导致电极表面最大von Mises 应力值的增加,因此在极耳选材应尽量选用杨氏模量低且泊松比较大的材料。

