摩擦系数及模角对钨合金静液挤压过程的影响研究

王俊杰，杨 建，成小乐，，丁露露

(1.西安工程大学 机电工程学院，陕西 西安 710048；2.中国重型机械研究院股份公司，陕西 西安 710032)

0 前言

钨合金是一种球形的钨颗粒和Ni、Fe以及少量的其他元素组成的粘结相在高温下烧结而成的一种双相合金，所以钨合金具备高强度、高密度、较好的韧性、高耐磨性和高耐腐蚀性等优异性能[1-3]。W-Ni-Cu系钨合金具有良好的射线吸收能力[4]，可作为辐射屏蔽材料，W-Ni-Fe系钨合金较W-Ni-Cu系钨合金具有更好的延展性和塑韧性等[5, 6]，被用于军事领域中的装甲、防弹材料等。而且高密度钨合金也被作为硬质合金来使用，且其导电、导热及焊接性良好[7]。亦可以将其作为镀层均匀覆盖在基材表面，有效保护基材不受腐蚀，所以被也广泛用于油田中的钻杆及油管中[8]。

钨合金的成型工艺有锻造、快速热挤压等。锻造技术可以进一步增强钨合金的力学性能，经过锻造工艺的95WNiFeCo钨合金具有更高的密度，强度和高密度[9-11]。通过快速-热挤压工艺，钨合金的综合力学性能较烧结态合金显著提高，而且初始晶粒尺寸对挤压后合金性能影响非常显著[12]。有学者采用快速热挤压技术对细晶93W-4.9Ni-2.1Fe-0.03Y%进行变形强化，发现快速热挤压有效降低了钨合金的应变速率敏感性[13]。通过锻造工艺和快速热挤压技术的钨合金力学性能有所提高，但由于一些新的应用领域对钨合金制品有了更高的要求，传统的加工方法很难满足更高品质的要求，比如，传统的挤压加工方法由于坯料与模具间存在剧烈摩擦，导致成型的制品表面质量不好，其强度降低等。静液挤压工艺有助于获得组织和力学性能优异的、符合高标准需求的材料。通过静液挤压变形后钨合金性能更好，抗拉强度、屈服强度显著提高[14]。比较静液挤压和旋锻工艺，发现静液挤压工艺可以实现钨合金的大变形强化，使其微观组织纤维化，钨合金材料的性能得到大幅度提高[15]，而且在变形量相同时，经静液挤压加工后的钨合金性能更优异，所以静液挤压工艺优于普通的旋锻工艺[16]。

针对钨合金的优异性能和静液挤压特有的优势，本文主要研究摩擦系数及模具角度对钨合金静液挤压过程的影响机理，为钨合金投入实际生产作理论参考。

1 模型的建立

本文针对93钨合金棒材的成型过程进行数值模拟，在模拟过程中，简化模型可以减少模拟计算的运算量，进而缩短了计算时间，本文在钨合金静液挤压成形过程中，取工模具及坯料的装配体为四分之一模型进行模拟计算。简化后的装配图如图1所示，其次将装配图生成STL格式保存，分别将各个零件导入Deform-3D中，生成模拟计算模型。此次模拟主要针对93钨合金，所以将坯料设置为塑性体，将工模具设置为刚性体。各个零部件的运动关系为，挤压轴被设定为主动件，坯料为从动件，凹模、挤压筒静止不动。

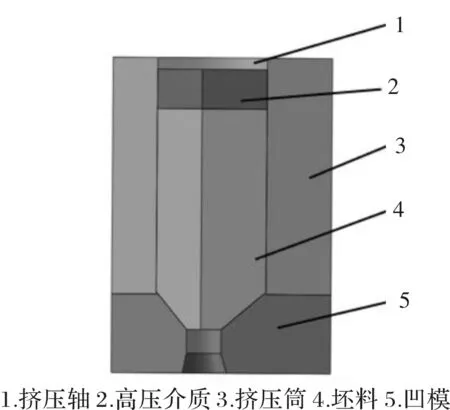
图1 工模具简化图

1.1 钨合金材料模型

本文中材料用93钨合金，其组成成分为93%W-4.9% Ni-21% Fe，其弹性模量为360 GPa，流动应力为0.92 GPa，泊松比为0.29。由于Deform-3D软件材料库中没有93钨合金的材料数据，首先需要建立93钨合金材料的力学模型，材料模型采用多线性随动强化模型。根据文献[17]中应力-应变关系曲线建立材料力学模型。

1.2 网格划分

由于主要针对塑性材料坯料计算分析，所以只对坯料进行网格划分。网格的数量和大小要有一个合理的值，网格太疏会导致计算不准确，结果太粗略；网格太细虽然会使计算结果更加精确，但是同时也会导致计算量过大，甚至会使计算进行不下去，考虑计算精度和计算量，网格数量保持在20 000个左右，网格的最小单元长度为7.5 mm。

2 工艺方案

本文采用单因素变量分析法分析坯料与模具间的摩擦因数μ，凹模锥角的模具角度α对挤压过程中钨合金棒材各场变量的影响，模拟中所用的基本方案参数设置如表1所示，根据Deform-3D软件模拟的结果，将有关数据导出并作出相应曲线图。

表1 有限元模拟工艺方案参数设置

3 结果与讨论

传统的挤压加工方法由于坯料与模具间存在剧烈摩擦，导致成型的制品表面质量不好，其强度降低等。静液挤压通过高压介质将力作用于坯料，所以坯料在成型过程中始终都处于很高的三向压应力中，这种压应力对于坯料变形极为有利，使得坯料在挤压开始前没有普通挤压的镦粗阶段，可以提高材料的塑性，能获得较大的挤压变形量，可较大幅度改变挤压制品的围观组织和性能。研究摩擦因数、模具角度两个工艺参数对钨合金静液挤压过程(平均应力、等效应变、挤压力)的影响。

由于模具出口处的坯料平均应力、等效应变等对模具参数优化及挤压过程的参数控制很重要，所有节点的选择均在模具出口处。在每一组模拟试验中的模具出口处分别提取坯料20个点的平均应力、等效应变、金属流动总速度的值，然后分别求每一组数的均方差SD值，即用所求得的每一组SD值来分别表示各个场变量的均匀性[18,19]，其定义如公式(1)所示。SD值越小，说明均匀性越好，反之越差。

(1)

3.1 摩擦因数对钨合金静液挤压过程的影响

3.1.1 摩擦因数对平均应力的影响

如图2所示为摩擦因数分别为0.1、0.15、0.2、0.3时，挤压过程进入到稳定阶段的情况下，坯料平均应力云图。从4个云图整体来看，挤压进行到稳定阶段后，坯料平均应力的变化都较为均匀，由于坯料和凹模间存在摩擦，则普遍在模具出口处平均应力分布最不均匀，应力值不太稳定，波动较大，且在模具出口处的平均应力值较大，甚至出现应力集中现象。还可以发现，平均应力的最大值很大，这很可能是因为在进行网格划分时，网格畸变引起的计算错误，由于在进行每一组模拟计算时的网格数目及划分方式都相同，所以在每组平均应力云图中都出现了平均应力最大值很大的情况。且在四个云图中可以看出，坯料表面没有出现平均应力最大值点，所以平均应力最大值应该出现在坯料内部。从图2a来看，挤压到稳定阶段后，平均应力值基本保持在一个稳定值，在模具与坯料接触的部分平均应力变化虽然不均匀，但是相比其他摩擦因数下的变化，平均应力值较小，因为摩擦因数较小时，坯料与凹模间的摩擦力较小，坯料变形的阻力较小，其应力分布也就越均匀。从图2b中可以看出，坯料被挤出进入稳定阶段后，平均应力也基本保持稳定。从图2c可以看出平均应力值较大且保持稳定，在模具出口处的平均应力分布最不均匀。从图2d中可以看出，在模具出口处平均应力分布也不均匀，且有两处应力值明显较大，在此处很可能出现应力峰值，在坯料被挤出进入稳定阶段后，平均应力值较稳定且保持在1 000 MPa左右。随着摩擦因数的增大，坯料与凹模间摩擦力也逐渐增大，使坯料的变形越不均匀，平均应力的分布也越不均匀，摩擦因数越大越不利于坯料的成型。因为坯料还没进入凹模定径带时，凹模与坯料间的摩擦力只存在于凹模的锥角部分，摩擦力较小，坯料的变形阻力较小，平均应力的分布较均匀，在进入凹模定径带后，增加了凹模定径带与坯料间的摩擦力，坯料变形阻力增大，坯料变形不均匀，平均应力分布相对也越不均匀，在挤压过程进入到稳定阶段后，坯料已经成型，坯料的平均应力相对较稳定。

图2 不同摩擦因数下各个场变量云图

如图3所示为模具出口处不同摩擦因数下平均应力的SD值变化曲线，从该曲线图可以看出，随着摩擦因数的增大，平均应力的SD值是逐渐增大的，摩擦因数为0.1时的SD值最小，此时的均匀性最好，当摩擦因数为0.3时，平均应力的SD值最大，此时的平均应力均匀性最差，说明摩擦因数越小，对应的平均应力的均匀性越好，反之，平均应力均匀性越差。摩擦因数小，则凹模与坯料间的摩擦相对也小，坯料成型过程中受到的阻力小，平均应力分布更加均匀，且不容易出现应力集中现象。

图3 不同摩擦因数下平均应力的SD值变化曲线

3.1.2 摩擦因数对等效应变的影响

如图4所示为摩擦因数为0.1、0.15、0.2、0.3时坯料在挤压进行到稳定阶段下的等效应变云图。从图4来看，等效应变值普遍较大，且整体等效应变分布相对较均匀，在进入模具定径带开始变形后等效应变值增大，在模具定径带处的等效应变分布最不均匀，应变的最大值也会在此处出现。从图4a看出由于摩擦因数较小，在坯料的成型过程中，等效应变的变化较均匀，且其在模具出口处的变化也最为均匀。从图4b看出此时在模具出口处的等效应变不太均匀，在此处坯料表面的等效应变值较大，很可能会出现等效应变峰值。从图4c看出等效应变分布也较为均匀，但是此处的等效应变值较之前有所增大。从图4d看出此时摩擦因数较大，相对应的摩擦力也增大，所以在模具定径带附近的等效应变分布最不均匀，且这种不均匀现象多发生在坯料表面，坯料表面的等效应变值大于坯料内部的等效应变值，这是在挤压过程中坯料表面受到较大的摩擦力所致。随着摩擦因数的增大，凹模和坯料间的摩擦力也增大，增大坯料的变形阻力，等效应变逐渐减小。

图4 不同摩擦因数下的等效应变分布云图

如图5所示为模具出口处不同摩擦因数下坯料等效应变的SD值变化曲线图，表示在不同摩擦因数下等效应变的均匀性。从图中可以看出当摩擦因数为0.1时坯料等效应变的SD值最小，即在摩擦因数为0.1时坯料等效应变分布最均匀，摩擦因数大于0.1时的等效应变SD值普遍较大，意味着摩擦因数较大时等效应变分布不均匀。因为摩擦因数增大使得坯料变形阻力增大，坯料变形过程中的均匀性下降，等效应变的分布变得不均匀。

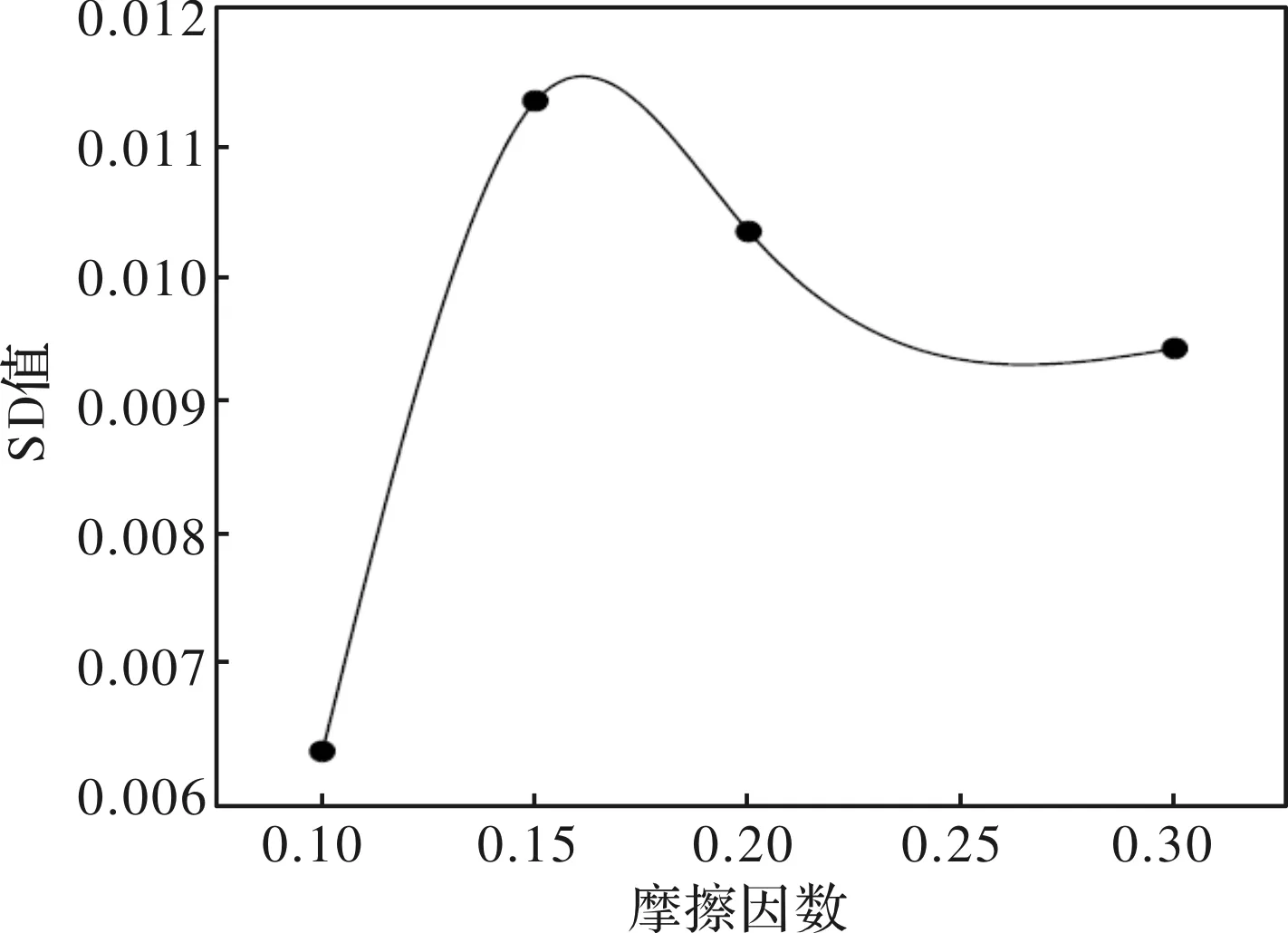
图5 不同摩擦因数下等效应变的SD值变化曲线

3.1.3 摩擦因数对挤压力的影响

如图6所示为不同摩擦因数下的挤压力变化，从图中可以看出在整个挤压过程中挤压力刚开始都是缓慢增加的，随着挤压时间的推移，挤压力逐渐增大且出现较大的波动，这是因为坯料被挤出凹模定径带时需要较大的挤压力，不同摩擦因数下的挤压压力变化趋势基本相同，并且摩擦因数为0.1和0.15时的挤压力相较于摩擦因数为0.2和0.3时的挤压力较小，这是因为静液挤压中剪切摩擦力仅仅存在于凹模与坯料接触部分，整个挤压过程中的挤压力相对普通挤压要小很多，所以在静液挤压中凹模与坯料间的摩擦因数对挤压力的影响较小。

图6 不同摩擦因数下的挤压力变化曲线

3.2 模具角度对钨合金静液挤压过程的影响

3.2.1 模具角度对平均应力的影响

如图7所示为挤压进行到稳定阶段时，模具角度分别为45°、60°、90°、110°时坯料平均应力的分布云图，从4个图整体来看，模具角度为45°时坯料平均应力值最小，模具角度为60°时坯料平均应力有所升高，模具角度为45°和60°时模具出口处的平均应力分布较不均匀。模具角度为90°和110°时，坯料平均应力整体较高，但是在模具出口处坯料的平均应力分布较均匀。因为随着模具角度的增大，金属材料的流动阻力增大，可能引起网格畸变增大，平均应力也随之增大。

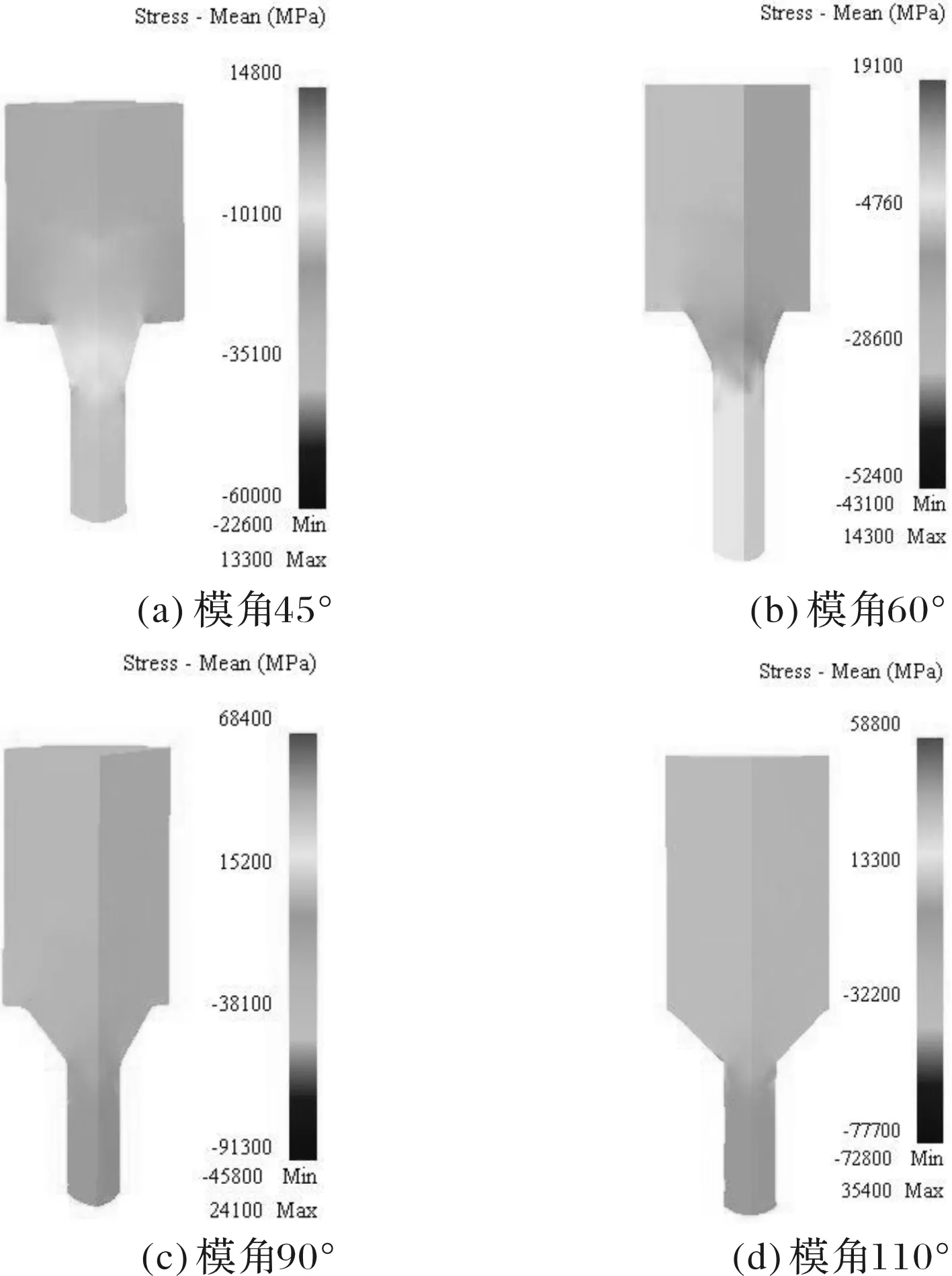
图7 不同凹模角度下坯料平均应力分布云图

如图8所示为在模具出口处，不同模角下坯料平均应力SD值变化曲线，在模角为45°和60°时，坯料平均应力SD值较小，说明此时的平均应力分布较均匀，随着模角增大坯料平均应力SD值也增大，在模角为110°时坯料平均应力SD值最大，此时的平均应力均匀性较差，初步说明坯料在模具出口处的模角增大，平均应力均匀性有所下降。因为在模具角度较小时，凹模锥面的长度减小，金属材料的流动转折较小，流动较为顺畅，坯料的成型质量较好，平均应力的分布均匀性也越好。

图8 不同模角下坯料平均应力SD值变化曲线

3.2.2 模具角度对等效应变的影响

如图9所示为挤压进行到稳定阶段时，模具角度分别为45°、60°、90°、110°时坯料等效应变分布云图。从图9可以看出，模角为45°时坯料等效应变分布不均匀，在坯料成型后边缘处最不均匀，此时的坯料等效应变值较小。模角为60°、90°及110°时等效应变分布相对较均匀，且随着模角的增大等效应变值越来越大，在模角大于45°后，坯料等效应变增长幅度很小。

如图10所示为模具出口处不同模角下坯料等效应变SD值变化曲线，模角为45°时的坯料等效应变SD值最小，随着模角增大坯料等效应变SD值也增大，说明模角为45°时坯料等效应变均匀性较好，随着模角增大坯料等效应变均匀性降低。随着模具角度的增大，金属材料在流出模具出口处时的阻力越大，越不利于坯料的成型，不利于材料的动态再结晶，坯料成型质量差，其等效应变的分布也越不均匀。

图10 不同模角下坯料等效应变SD值变化曲线

3.2.3模具角度对挤压力的影响

如图11所示为不同模角下挤压压力的变化曲线，从下图可以看出，模角为45°时挤压力变化最平稳且挤压力最小，模角为90°和110°时挤压力的变化趋势大致相同，波动较明显。随着模角增大挤压力也增大，且挤压力波动较大越不稳定，一般情况下模角越大，则金属的流动越不均匀，从而使金属的变形功增加，挤压力增大，相反，模角较小，则使金属流动较均匀，从而使金属变形功降低，挤压力减小[20]，但是因金属坯料与模具接触面积增大，则使摩擦力增大，挤压力反而会增大，所以，模角只有在合适范围内才可以使挤压力最小，由以上分析可知，在进行模具设计时，模具角度的选择不宜过大，本文中为45°左右较佳。

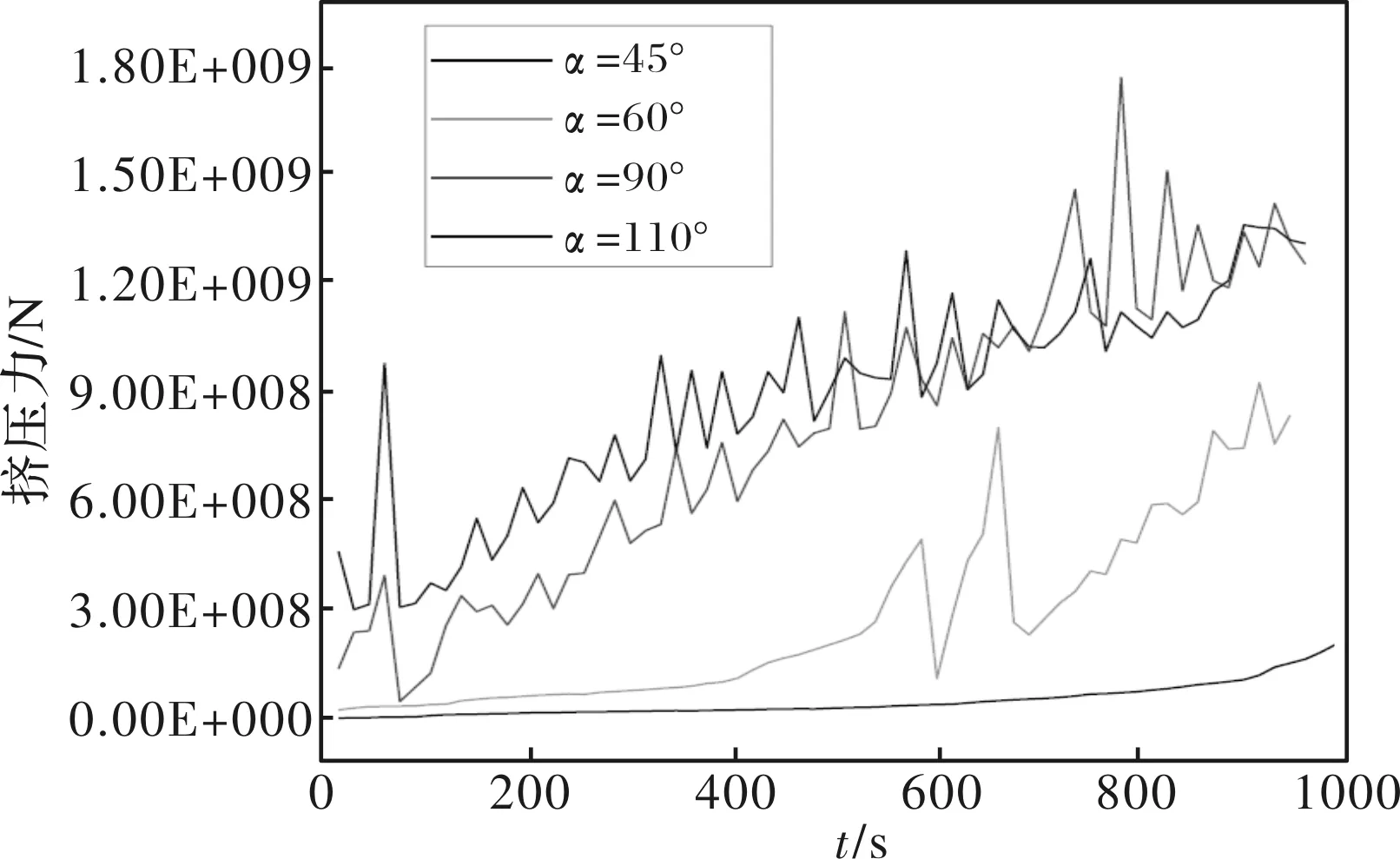
图11 不同模角下挤压压力的变化

4 结 论

研究摩擦因数及模具角度工艺参数对钨合金的静液挤压过程的影响，得出如下结论。

(1)模具出口处，摩擦因数为0.1时坯料平均应力的均方差SD值最小，此时坯料平均应力分布最均匀，随着摩擦因数逐渐增大，平均应力分布均匀性越差，摩擦因数对金属的流动速度影响较小

(2)模角为45°时坯料等效应变均匀性最好，随着模角增大坯料等效应变SD值也增大，等效应变均匀性降低。模角为45°时金属流动速度最小，模角大小对金属流动速度影响不明显。模角为45°时挤压力变化最平稳且挤压力最小，挤压力随模角增大而增大。

(3)对于钨合金静液挤压，摩擦因数的参考选取范围为0.05～0.1；模具角度可以选择45°或略小于45°。