兆瓦级直驱风力发电机组塔筒涡激振动分析
曹垚鑫,赵 迪,李彦蓉,昝志龙
(1.中国质量认证中心,北京 100070;2.北京长征高科技有限公司,北京 100176;3.北京航星机器制造有限公司,北京 100013;4.国电联合动力技术股份有限公司,北京 100089)
0 前言
风能作为一种清洁能源,得到世界各国的重视和开发利用。塔架作为风力发电机组的支撑结构,同时吸收机组的震动[1]。塔架主要有锥形钢筒、桁架、钢筋混凝土和混合塔架等形式,但锥形钢筒得到广泛应用。风吹过锥形钢筒的圆形截面形成漩涡[2],漩涡脱落激起塔筒垂直于来风方向上的振动,称之为涡激振动(Vortex Induced Vibration)。长期的涡激振动会对塔筒静力强度和疲劳强度产生影响,尤其是当外载荷的频率与塔筒或整个风机结构的固有频率[3]一致时,会导致共振的发生。共振震动幅度大,会造成风力发电机组结构较大的疲劳损伤,降低塔筒寿命,甚至威胁整个风力发电机组的安全[4]。国内外主要采用流体动力学技术,使用数值模拟方法计算大气边界层中绕流,研究涡激振动问题。Jamal和Dalton采用LES方法计算因漩涡发放的引起振动;陈文礼采用RANS方法对涡激振动进行了数值模拟;赵德有应用Newmark算法计算桅杆的涡激振动响应;李德源应用有限元方法分析塔筒在非定常气动力下的动力学响应;王红梅采用两参数模型研究了高耸结构的气-固耦合作用[5];董占琢[6]应用流体力学和有限元方法分析了塔筒的横向振动问题。
本文以锥形钢筒塔架为研究对象,采用结构动力学方法分析兆瓦级直驱风力发电机组塔筒的固有特性,得出不同安装状态下塔筒的固有频率和固有振型;通过解析算法分析塔筒涡激振动,得出塔筒共振时的临界风速、最大横向振幅以及综合受力情况[7,8];根据疲劳强度等级,分析塔筒焊缝的疲劳损伤,校核塔筒焊缝的疲劳强度。为兆瓦级风电机组的塔筒设计、安全吊装和维护提供理论依据。
1 塔筒固有频率和振型分析
根据兆瓦级风力发电机组的实际安装过程,每安装一段塔筒,以及安装完成、维护时的整机都需要进行涡激振动分析,分析塔筒共振时的固有频率和固有振型。
风力发电机组中转动与不转动部件的模态特性是独立的。被动响应分析中,以运动方程来耦合部件模态,耦合的运动方程为[9]
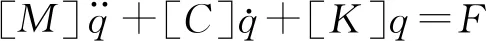
(1)
式中,[M]为模态质量;[C]为阻尼;[K]为刚度矩阵;q为模态向量;F为模态力向量。
根据不同安装状态风力发电机组的质量模型、机舱、发电机、叶轮的转动惯量以及塔筒模态阻尼因数,分析得到不同安装状态塔筒的一阶固有频率和振型。
2 涡激振动分析
2.1 考虑涡激振动的判定条件
当涡激振动处的平均风速Vm不小于共振发生时0.8倍的临界风速Vcrit,i时,需考虑涡激振动效应,即
Vm≥0.8Vcrit,i
(2)
式中,Vm为涡激振动处(取距离塔顶当前安装状态下3倍的塔筒顶部直径的位置)一年一遇(10 min平均值)最大风速;Vcrit,i为第i阶共振发生时的临界风速。
(3)
式中,d为共振时塔筒挠曲最大位置的外径;f为塔筒的固有频率;St为斯德鲁哈尔数,取0.18。
2.2 塔筒最大横向振动幅值
塔筒发生共振时,最大横向振幅有两种计算方法。
(1)方法一。GL2010[10]中被推荐使用的塔筒在临界风速下最大振幅 计算。
(4)
式中,Sc为斯克鲁顿数;K为振型系数,取0.13;Kw为有效相关长度系数,见公式(5);clat为侧向力系数。Sc和clat根据临界风速的雷诺数从EN 1991-1-4∶2005[6]中取值。
有效相关长度系数Kw为
(5)
式中,L1为相关长度,取当前安装状态下6倍的塔筒顶部直径;hp为塔筒高度。
(2)方法二。欧盟规范中塔筒在临界风速下最大振幅yF,max计算方法,该方法更适用于兆瓦级风力发电机组的涡激振动分析。
(6)
式中,Cc为截面形状的气动常数;Ka为气动阻尼常数,与湍流强度有关;aL为常数,取0.4;h为塔筒高度;Cc和Ka从EN 1991-1-4:2005[11]中取值。
2.3 塔筒横向力和倾覆力矩
不同状态下塔筒受到的横向作用力为振动惯性力Fw的反作用力,高度z处单位长度上的惯性力Fw(z)为
Fw(z)=m(z)·(2πf)2·φz·yF,max
(7)
式中,m(z)为高度z处塔筒单位长度质量;φz为塔筒模态归一化后高度z处的位移。
塔筒高度z处倾覆力矩为
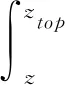
(8)
式中,ztop为不同安装状态下塔筒顶部高度。
3 塔筒焊缝疲劳损伤分析
3.1 塔筒截面弯曲应力
塔筒主要受弯矩作用,截面受弯矩作用下的弯曲应力、剪应力以及z方向的压应力的影响,但是弯曲应力所占比重较大,故只考虑截面弯曲应力的影响[12]。塔筒截面弯曲应力为
(9)
式中,R为截面外径;r为截面内径。
3.2 塔筒焊缝许用循环次数
焊接结构的S-N曲线由指数斜率分别为3和5的两条线组成[13]。通常焊缝结构定义为在2×106次循环下的特定疲劳强度,并定义疲劳等级(detail category,DC)为71 MPa[14]。为了计算方便,简化焊缝的S-N曲线为指数斜率为4的直线,根据拐点ND=5×106,经推导,不同截面焊缝的许用循环次数Na为
(10)
式中,Δσ为疲劳应力幅值。
3.3 塔筒焊缝疲劳损伤
在规定的疲劳寿命周期内,塔筒涡激振动的疲劳循环次数N为
(11)
式中,T为使用期限(单位为秒),其值等于3.2×107乘以预计使用年限(单位为年);ny为塔筒固有频率;ε0为涡激振动风速带的带宽系数,取值0.3;V0为出现涡激振动处的特征平均风速的20%,即年平均风速。
基于Palmgren-Miner线性累积损伤原理[15,16]对疲劳失效问题进行分析,塔筒焊缝疲劳累积损伤D为
(12)
式中,γm为局部安全系数,取值1.265。
如果塔筒焊缝的疲劳累积损伤D<1,说明塔筒疲劳设计是安全的,涡激振动不会对塔筒产生疲劳破坏;如果塔筒焊缝的疲劳累积损伤D>1,说明涡激振动会使塔筒发生疲劳损坏,是不安全的。
4 工程实例分析
本文针对兆瓦级风力发电机组机组塔筒进行涡激振动分析。塔筒高度73.1 m,塔底直径4.2 m,由三段塔筒通过法兰螺栓连接。风电场空气密度1.206 kg/m3,年平均风速6.2 m/s,轮毂高度处一年一遇最大风速(10 min平均值)为30 m/s。对不同的安装状态进行涡激振动分析,见表1。
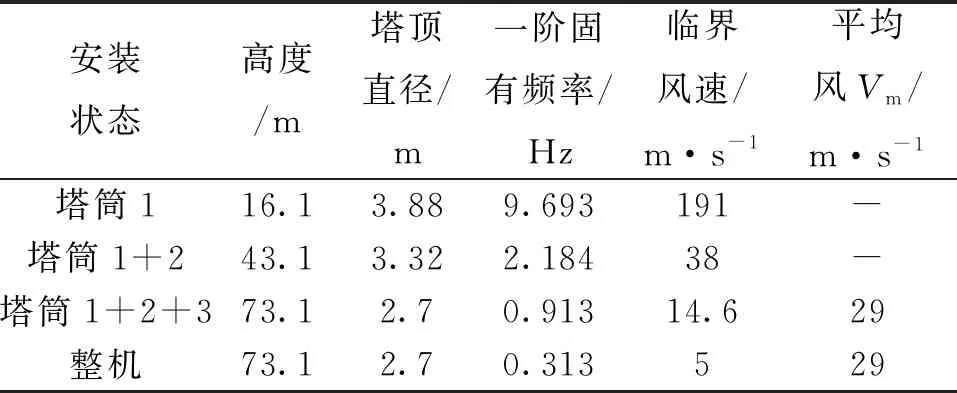
表1 涡激振动分析相关参数
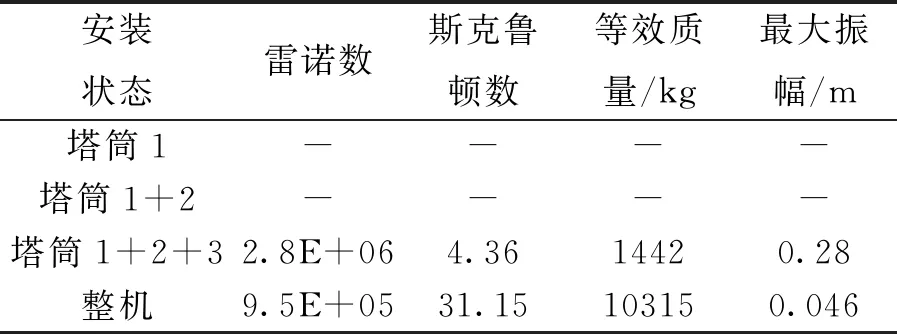
表1 涡激振动分析相关参数(续)
根据判定条件,状态1和状态2无需进行涡激振动分析。分别用GH-Bladed和有限元方法对状态3和状态4进行固有特性分析,误差0.56%,可见两种方法均适合塔筒的固有特性分析。但是在最大振幅的计算中,采用方法一计算状态4最大振幅为0.039 m,采用方法二为0.046,误差为15%,考虑风场的实际情况,取最大振幅0.046进行涡激振动分析。状态3和状态4分别进行一年的疲劳损伤计算,状态3的疲劳损伤见表2。状态4的疲劳损伤特别小,可以忽略不计。
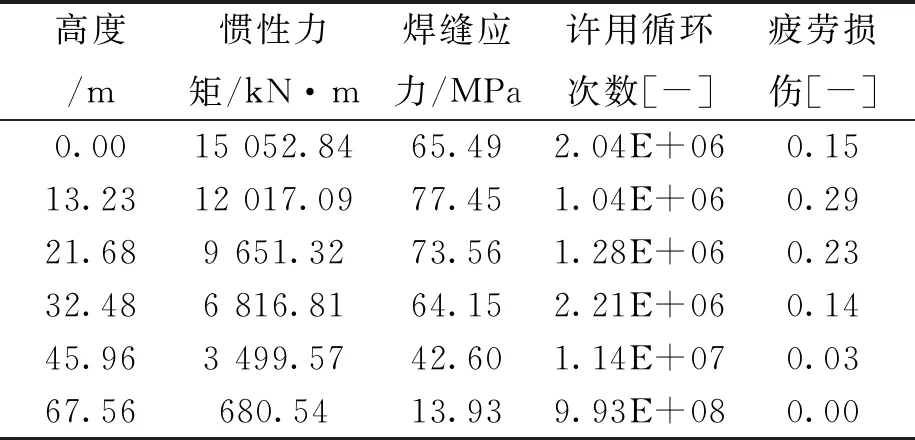
表2 状态3疲劳损伤相关参数
5 结论
随着风电高塔筒技术的发展,塔筒高度的增加会导致整体刚度降低且固有频率减小,塔筒的涡激振动影响越来越明显。采用结构动力学分析方法获得塔筒固有特性,通过解析算法,结合风场实际情况分析共振时塔筒横向最大振幅和受力情况,对塔筒焊缝疲劳强度进行校核。
当兆瓦级机组进行吊装时,涡激振动使塔筒产生较大的惯性力和倾覆力矩,增加塔筒焊缝的疲劳损伤。考虑塔筒涡激振动的影响,不仅要避开临界风速,更需严格控制吊装进度,并逐节进行涡激振动分析,校核塔筒焊缝的疲劳强度。

