带正参数的非局部Kirchhoff方程解的存在性研究

陈海燕

（湖南工程学院 计算科学与电子学院，湘潭 411104）

0 引言

非局部Kirchhoff方程起源于Kirchhoff在研究弹性弦的自由振动过程中，提出的一种具有实际应用背景的数学模型［1］.自模型建立开始起，就在物理、力学、医学等诸多领域广泛应用，因此吸引了众多学者对此进行深入研究.

2018年严忠权，柳鸠等［2］研究了一类具有一般临界增长的自治的Kirchhoff型方程，利用Schro¨dinger方程以及Pohozaev等式得到方程具有一个径向对称的正基态解：

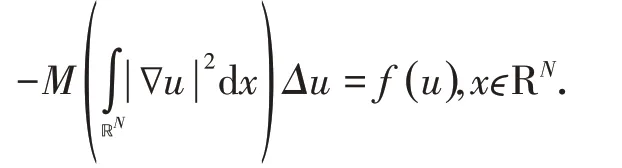
2020年蒲洋等［3］研究了在有界区域上的一类带Sobolev紧临界指数的Kirchhoff型四阶椭圆方程.当非局部项Kirchhoff项可退化时，利用变分方法，获得了该方程对应能量泛函的一个全局极小值点，从而找到了该方程的一个非平凡解：

2020年王跃，周荧等［4］在全空间上考虑一类含有临界指数的非局部Kirchhoff型问题，利用分析技巧和特殊函数研究其古典解的存在性：

本文基于前者研究的基础，重点讨论非局部Kirchhoff型方程，当参数λ＞0时，对研究非局部方程解的存在性的影响.

1 方程的存在性证明思路

本文研究的方程是由Kirchhoff在1883年研究弹性弦振动时提出的数学模型，重点描述了可伸缩绳的横向振动的长度变化，具有一定的物理背景.

Nonlocal―Kirchhoff型方程形式如下：

其中，D⊂R n，区域,D为有界区域，，指数p＞0，空间维数n≥1，非局部算子［5］定义如下：

根据变分法相关定理［6］，原方程（1）解的存在性问题转变为求解对应的能量泛函的临界点问题：

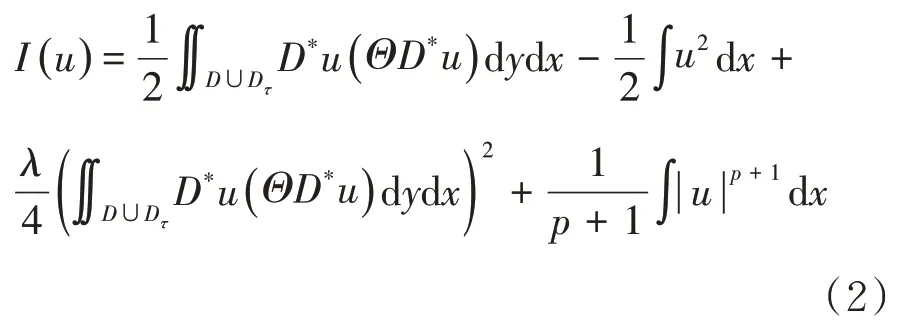
考虑参数λ为正数时，借助临界点理论，首先，证明能量泛函有下界.其次，能量泛函在空间中存在弱收敛序列.第三，结合Sobolev紧嵌入定理［7］、Riesz定理、Fatou引理，推导出弱收敛序列是强收敛序列，且收敛点即为能量泛函的临界点.

2 方程解的存在性证明过程

2.1 能量泛函的可微性

定理1能量泛函I(u)是Fre˙chet可导的.

证明：

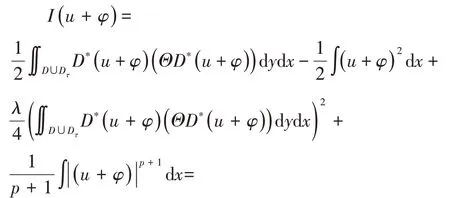
故泛函I(u)在空间Fre˙chet可微.

2.2 能量泛函存在临界点

定理2若，则I(u)在中有下界.

证明：非局部能量空间V(Ω∪Ωτ)等价于分数阶空间，则对应的空间范数等价，即：

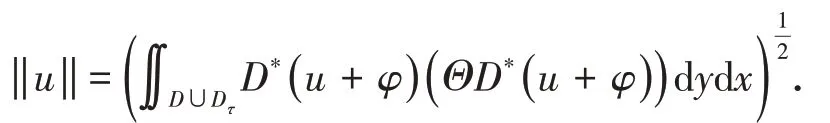
根据确界原理，I(u)存在下确界.故存在，使 得，则 称{u k}是I(u)的极小化序列.

定理3若{u k}是I(u)的极小化序列，则{u k}是中的有界序列.

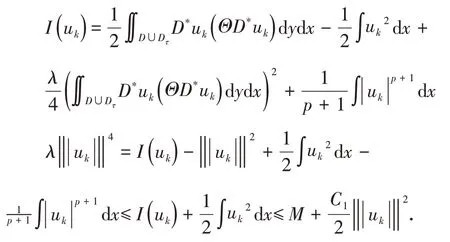
由于λ＞0，根据上述不等式，证得{u k}是中的有界序列.

定理4若{u k}是中的有界序列，是自反可分的空间，则{u k}在中弱收敛到u 0，且

证明：根据I(u)的定义知，要证明即需要证明

若能验证下列不等式方程组均成立，则上述不等式成立：

证明①②.由L2(D∪Dτ)空间范数的弱下半连续性，且由Sobolev嵌入定理，空间紧嵌入L2(D∪Dτ)空间，即可证明.

证明④，首先，由I(u)是有界，‖u‖有界以及有界，可知有界.因为，根据Sobolev嵌入定理是紧嵌入到L2(D∪Dτ).

由Riesz定理，存在子列{u k}.

根据Fatou引理：

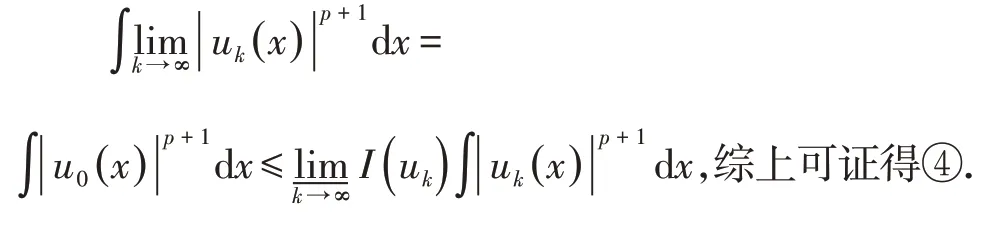
定理5存在，使得即u0是问题（1）的解.

证明：u k在中存在弱收敛的子列，设其弱极限为u0，再根据定理4I(u)的下半连续性，有则故 存 在使 得，即u0为I(u)的临界值点，u0是问题（1）的解.

3 结束语

在本文中，考虑的是在有界区域D上的非局部Kirchhoff方程，后续可以考虑从有界区域拓展到全区域Rn，研究方程解的存在性.另外后续可以进一步考虑方程解的适定性问题的其他内容，例如是否存在非平凡解，解在区域上的连续性以及能否利用第一特征值的定义，讨论特征值与方程解的关系，进而对第一特征值进行估计.