用画说话,以画促思
黄城红 吴雪斐





“倍”是小学数学中的一个基础概念,是各个版本教材的“种子课”。各版本教材虽然选取的素材不一样,但编排思路类似,都是先用一个例题来教学“倍”的基本概念,再通过给定的练习来巩固概念。在教学之前,我们有如下思考。
1.学生的学习主动性如何发挥。在几个版本教材的编排中,都是通过“例题+练习”的模式来进行教学。这种固有的学习节奏,学生被牵着鼻子走,牵到哪里,学到哪里。学生的学习主动性没有得到发挥,原有的学习经验无从利用,创造性被限制,处于一种被动的学习状态中。
2.学生的思维能力如何培养。数学是抽象的,如何在教学过程中培养学生的抽象概括能力、建模能力?如何通过画有意义的图,让学生在直观与抽象之间进行自然的转化,培养学生的思维能力?如何更好地把“倍”的学习纳入数学学习的整体结构当中?基于如上思考,我们进行了如下教学实践。
一、“倍”的初体验
师:同学们,今天我们来学习一个新的教学内容。请看黑板,认识这个字吗?(板书:倍)
生:我知道,它的意思就是谁是谁的几倍……
师:那我就来考考你们。请看,屏幕上有两个三角形,你们能画圆,使圆的个数是三角形的3倍吗?
(学生趣味盎然地画圆。教师请3个同学在黑板上展示画法并介绍想法)
生:我是这样想的,三角形有2个,它的3倍就是二三得六,所以我就画了6个圆(如图1所示)。
生:我也是这样想的,三角形有2个,它的3倍就是3个2,也画了6个圆(如图2所示)。
生:我也是这样想的(如图3所示)。
师:他们画的都是6个圆,但所画的图还是有区别的,看到这几幅图,你们有什么想说的?
生:我最喜欢图2,因为在每2个圆之间用一条虚线隔开了。这样就看得很清楚,圆有3份,就表示3倍。
生:我更喜欢图3,用圈把每一份数都圈起来了,这样就能很清楚地看出,圆的个数是三角形的3倍。而且我还发现,图1、图2只画了圆的数量,图3把三角形的数量也画出来了,这样就说明圆的个数是三角形的3倍,而不是其他图形的3倍,这样表示的意思更准确。
(学生鼓掌表示赞同)
师:从掌声来看,同学们认为既要把原有的三角形画出来,又要把每两个圆为一份做标记。从图3就可以清楚地看出,2个三角形是一份数,圆形的个数有这样的3份,就表示圆的个数是三角形的3倍。
【评析】在这个教学环节中,教师利用学生已有的知识经验,“诱导”学生把“倍”的意思用图表达出来。在学生把各自的想法用图表示出来后,再引导学生对所画的图进行比较、总结,让学生初步、准确地建立倍的概念:倍,要先明确一份数,再看有这样的几份,就是几倍。通过学生主动、直观的表达,观察和比较,初步理解和建构“倍”的概念。
二、明确“倍”的概念
师:看来同学们会画2个三角形的3倍了,你们还会画正方形,使正方形的个数是这2个三角形的4倍吗?
(学生很快画出图,如图4)
生:把这2个三角形圈起来,就是一份。画4个圈,每个圈里有2个正方形,就表示有4个2,正方形的个数就是三角形的4倍。
师:这2个三角形的3倍、4倍会画了,那你们还会画这2个三角形的多少倍?
生:我还会画这2个三角形的5倍、6倍、7倍……
(学生说完很快地画出图,如图5所示,并解释道:2个三角形圈成一份。现在画了5个圈,每个圈里有2个涂阴影的圆,涂阴影的圆的个数就是三角形的5倍)
师:这个时候你们对“倍”有什么样的认识?
生:我觉得“倍”跟我们以前学的乘法是有联系的。请看,3倍就是3个2,4倍就是4个2,5倍就是5个2……
师:这个同学总结得非常好!从这些图中我们确实可以看出,一个数的几倍就是几个几。
【评析】在这个教学环节中,教师顺应了学生的思路,一份数的量“2个”保持不变,引导学生依次画出2个三角形的4倍、5倍……通过画直观图,学生就容易自主地概括出倍的本质含义:在保持一份数不变的情况下,有几份就是几倍。这个教学过程,没有教师的强加,而是学生自主体验后的自然概括,让“倍”的概念教学水到渠成。
三、升华“倍”的认识
师:对于“倍”的认识,你们还有什么问题吗?
生:刚才我们画的图里,都是每个圈里只有2个三角形。每个圈里可不可以是3个、4个、5个……三角形呢?
师:这个同学提的问题非常好!如果现在一个圈里画了3个三角形,那它的3倍怎么表示?
生:那就在下面一行画3个圈,每个圈里要画3个圆。
(学生画出图,如图6)
生:通过画图我明白了,图6中下面一行,每个圈里圆的个数,都要和原來一份数的个数一样多。下面每个圈里圆的个数,是由上面圈里三角形的个数决定的。如果上面那个圈里三角形有4个,那下面一行中每个圈里的圆也有4个;如果上面那个圈里三角形有5个,那下面一行中每个圈里的圆也有5个,以此类推。
师:这个圈里可以放几个三角形或者几个圆?
生:可以是1个,也可以是2个,还可以是3个……甚至是无数个,但不管是几个,用圈圈一下,就表示一份数。
师:看来这个圈的本领真不小啊,还能圈无数个三角形!
生:我现在明白“倍”的意思了。先圈出一份数,这个一份数可以是1个,可以是2个,也可以是3个……不管是几个,圈起来了就表示一份数,再看几个这样的圈,就是几倍。
师:这个时候,你们还有什么问题吗?
生:是啊,这个圈的本领可真大,能表示1个、2个、3个、4个……咦,假如这个圈里有100个三角形,画不下呢?这可怎么办呀?
师:这个同学的问题问得太好了!是啊,如果要在圈里画100个三角形,会画得很累的!怎么解决这个问题?
生(兴奋地):我想到了!可以用数来代替,就在每个圈里写数100。
师:你太棒了,你的想法真好!
师:除了画一个圈,在圈里写上数100表示一份数。还可以怎么画图,表示一份数是100?
生:可以画线段图,在每条线段上写上数100。
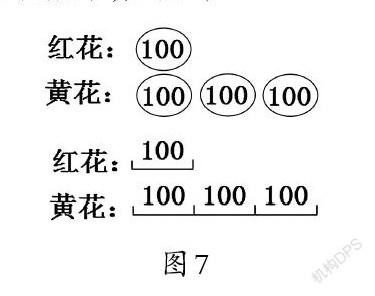
师:那就用你们喜欢的方法来表示:红花有100朵,黄花的朵数是红花的3倍。
(学生画图展示,如图7)
师:你们画得都非常好,都正确地表达了黄花的朵数是红花的3倍。当然,画线段图时,可以仿照这个同学的画法,把表示黄花的3段连在一起,这就是我们常用的线段图。
【评析】数学的本质就是抽象。在本教学环节中,在前面通过直观图表达倍的概念的基础上,又进一步抽象,还可以直接用数来表示物体的个数,让学生很自然地体会到,一份数不仅可以是一个物体,还可以是多个物体形成的一个整体,这样就准确、完整地建立了“倍”的概念,也为今后学习分数时,建立“单位1”的概念进行了铺垫和渗透。这个教学过程由学生自己的问题开始,顺着学生的思路顺藤摸瓜,逐步抽象、建模,一步一步地触摸“倍”的本质。这个过程,学生的学习主动性得以激发,创造性得以发挥,思维能力得以培养。
四、“倍”的整体结构
师:请同学们看下面这一幅图(如图8)。从图8中,我们很容易地看出有2个三角形、3个圆和6个正方形。根据这种3种图形的个数,你们能求解什么数学问题呢?
(学生先独立思考,讨论交流后进行汇报)
生:我知道,正方形的个数是三角形的3倍。
(学生说完就把两个三角形圈起来,还把6个正方形每2个为一份圈起来)
生:我知道,正方形的个数是圆的2倍。
(学生说完后同样用画圈的方法来表示他的想法)
师:咦,为什么一会儿说是2倍,一会儿说是3倍呢?
生:就是因为倍数不同。跟三角形相比时,一份数是2个,就画了3个圈,所以是3倍;跟圆相比时,一份数是3个,只能画2个圈,所以是2倍。
师:除了能说相互之间“倍”的关系外,还能说说它们之间的其他关系吗?
生:我还知道,圆比三角形多1个;反过来,三角形比圆少1个。
生:同样地,我还知道,圆比正方形少3个,正方形比圆多3个。
生:我还知道,圆的个数是正方形的一半。
师:这个同学的想法太不一样了!你说的圆的个数是正方形的一半,也是它们之间的一种关系。你知道“一半”怎么表示吗?
生:用[1/2]来表示。(说完就写出了分数[1/2])
师:你的知识太丰富了,这是我们以后要学习到的知识。随着学习的继续深入,我们将学到更多表示它们之间关系的方法。
【评析】这节课学生学习了倍的知识,知道了“倍”的含义,还理解了它是表示两个量之间的一种关系。但我们的教学不能停留于此,还有必要把“倍的关系”纳入“比较两个量之间关系”的整体结构中,帮助学生构建起系统性的知识体系。学生的能力是无穷的。当有学生说出“一半”的关系时,教师很自然地抓住了这个精彩的课堂生成,引出了分数的概念,这样,又把“两个数之间的关系”延伸到了一个更广的范围,为学生今后学习分数的知识埋下伏笔,也初步感知了“2倍”和“一半”的互逆关系。这个教学过程,教师的开放性提问,给了学生充分表现的机会,让学生能够站在整体和全局的角度,来理解和掌握倍的知识,做到“既见树木,又见森林”,这对于学生的整体认知是非常有好处的。
【课后总评】
这节课,学生学得主动、生动、灵动。在教师的大环节教学设计下,教学的资源都来自学生的自主画图。而在学生画图的过程中,做到了以下几个方面。
一、用画说话,由抽象到具体
“倍”是小学数学知识体系中表示数量关系中的一个基本概念,它表示的是两个数量之间的一种关系,所以各个版本教材中都有这个概念的教学。但它又是一个比较抽象的概念,仅靠语言是很难描述的。因此,在本课中,教师始终让学生把这个抽象的概念用图表示出来,通过直观图,学生就很容易地感知:一个数是另一个数的几倍,就是以前学过的乘法中的几个几。通过学生自主画图,可以有效地让学生把原有的经验顺畅地表达出来。学生在看到图后,也能更方便地进行总结,这是一个学生自我表达、自主建构的过程。总之,用画来说话,把抽象的概念直观化、具体化,便于学生理解和掌握抽象的倍的概念。
二、以画促思,由具体到抽象
学生通过画具体、直观的图形,理解和掌握了倍的概念,但学生的思维不能仅仅停留在直观的层次上,还必须进行深化和提升。為了让学生更深刻地理解倍的概念的本质,培养创造性解决问题的能力,教师又给学生创设了提问的机会,学生自然地顺势提出:“一份数可以是1个、2个、3个……甚至是无数个,画不完怎么办?”在这种矛盾的认知冲突中,充分地激发了学生的思维,发挥了想象能力。学生就想到可以不用画具体的物体了,而是用数来代替,并可以继续用圈图、线段图来表示。这样的教学过程,就让学生非常清晰地体验到数学抽象的本质,培养了学生的抽象思维能力,学生的思维水平达到一个新的层次。这个过程也让学生充分地认识到,这里的一份数可以是一个,也可以是多个,甚至是无数个,这就为今后学习分数时,更准确地建立“单位1”的概念做了很好的铺垫。
由此,我们的数学教学,要在抽象和直观之间进行转换。当学生理解有困难时,就要把抽象的概念直观化,帮助学生理解数学。而当学生掌握了基本的概念之后,又必须对直观进行适度的抽象,提升思维层次,感受数学的本质,这才是有意义的教学。
(作者单位:江西省南昌市铁路第一小学 广东省河源市源城区公园东小学)

