在知识关联中提升数学学习力

刘克群

数学学科是不可分割的有机整体，它的生命力正是在于各个部分之间的联系。尽管数学知识千差万别，我们仍然清楚地认识到，在作为整体的数学中，使用着相同的逻辑工具，存在着概念的亲缘关系。

就教材编排而言，各类数学教材为了编写的方便，往往突出了概念与命题之间的逻辑关系。教学中，教师应注重将数学的知识结构转化为学生的认知结构，帮助学生寻找数学知识之间的联系，用联系的观点进行分析与思考，无论面对怎样复杂的“未知”都能转化为已学的“旧知”，学会学习、学会思考、學会创造。教师只有帮助学生建立起整体性的知识结构，从宏观上整体把握数学内容，才能让学生比较清晰地认识数学知识之间的逻辑链条，感受数学内部结构的条理化、网络化和系统化。如何帮助学生主动关联建构知识，内化为自身认知结构，形成学习力呢？笔者认为可以从以下几方面进行思考。

一、纵向挖掘，整体建构

数学本身就是一个知识系统，数与代数、图形与几何、统计与概率等不同内容之间有着相互联系，同一部分内容不同知识点也有内在的逻辑关系。因而，在教学中，我们应重视帮助学生很好地突破单一认知结构，纵向挖掘知识之间的内在联系，从而从整体上建构知识，形成稳固的知识结构。

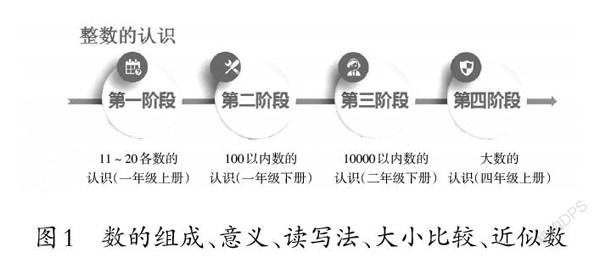
例如，以“整数的认识”这一内容为例（如图1），小学阶段整数的认识共分为四个阶段，分别为11～20各数的认识、100以内数的认识、10000以内数的认识、大数的认识。这四个阶段都有共同的认知点：数的组成、意义、读写法、大小比较、近似数。这样一种认知结构又可以推演至小数、分数的认识。无论是整数的认识、小数的认识还是分数的认识，它们都在遵循学生的认知规律。而整数的认识又是小数、分数认识的基础，整数的意义、位值制思想，整数的读写法、大小比较、近似数等都与小数、分数有着密切的联系，存在着概念的亲缘关系。

教学中，教师要引导学生按知识结构来建构知识，而这种建构又始终是开放的，促使学生触类旁通。而“11～20各数的认识”中的位值制思想又是整个数认识的基础。

同样，数的运算，无论是加、减、乘、除运算法则还是混合运算顺序以及运算定律，对于整数、分数、小数同样适用，其数学本质是一样的。

如图2，在整数加减法中，最关键的是20以内数的加减法，最基本的是10及10以内数的加减法。帮助学生理解算理、掌握位值制思想，是掌握数的运算的关键所在。因而，在数学教学中，教师要有“整体的眼光”，把教学过程的每个环节看作这节课的一个局部，而每节课又是整个单元或者教学阶段的一个局部;把每个教学单元或者教学阶段看作整个小学阶段的一个局部。教师只有从整体上把握知识之间的关联，才能更好地帮助学生把握知识的本质，为后续触类旁通、灵活运用知识打下坚实的基础。

二、横向串联，主动建构

数学学科的知识结构不仅是一个完整的纵向结构，还是一个有着前后关联的横向结构。在教学中，教师要引导学生将所学的知识主动进行横向串联，用联系的眼光多维度审视、建构，从而促进数学知识的认知结构主动形成。

以小学阶段图形与几何中的内容为例，图形几何一维、二维、三维空间三种度量单位的认识如图3所示。

在长度单位教学中，要体会统一长度单位的必要性，认识长度单位，用单位度量，解决问题;在面积单位教学中，要体会引入面积单位的必要性，认识面积单位，用单位度量，相关图形的面积计算;在体积单位的教学中，要体会引入体积单位的必要性，认识体积单位，用单位度量，相关图形的体积计算。度量的单位不同，但都会让学生经历体会统一单位的必要性，体验感悟理解单位价值与意义，并且利用单位进行度量。因此，在教学中，教师要横向串联知识体系，区分单位之间的特征不同（度量的对象不同），通过迁移、对比，真正把握单位的概念本质，从而主动建构知识，加强知识之间的内在联系，打通知识之间的脉络，形成稳定知识系统与网络，有助于学生将数学的学习相互关联。

同样，不同的图形在不同年段让学生认识，三年级认识长方形、正方形，四年级认识平行四边形、三角形。在教学中，教师应注意突破这种由教学先后次序所形成的逻辑线索的束缚，而应从更为广泛的角度揭示这些概念之间的内在联系，从而真正建立起整体性的概念体系。

三、灵活变通，激活知识

在理解知识的基础上掌握运用思想方法，有利于保持长久记忆以及技能和方法的迁移，建立稳固的知识体系。只有懂得灵活变通，激发主动建构的“元认知”，才能真正让学生将所学的知识变成知识源泉，从而实现真正意义上的学会学习、学会运用、学会创造。

例如，在古代应用极其广泛的建筑、器具、钱币等都体现了“外方内圆”“外圆内方”，教材中提及要求外方内圆或外圆内方之间部分的面积。教学中，教师让学生类比圆的面积、正方形的面积计算公式就能解决这个问题。教师先出示圆，提问：“圆的面积你会求吗？”（刚学完圆的面积）紧接着在圆外面出示一个正方形（外切），提问：“正方形的面积能求吗？”（学生三年级学过的知识）接着教师不是按照教材内容问学生圆与正方形之间阴影部分面积怎样求，而是追问：“会求圆的面积，也会求这个正方形的面积，那你还能求到什么吗？”“你还能求到什么吗？”一个看似简单的问题，却让安静的课堂活跃起来。学生思考片刻之后，马上举手回答，思维的火花在碰撞：“我能求到它们之间那四个不规则图形的面积（阴影部分面积）”“我能求到一个那样的图形面积”“我还能求到圆面积与正方形面积的比”。而这个关于“比”的问题有很大研究价值，这个“比”能让半径不同的圆的面积与正方形的面积计算变得简单，只要求到其中一个量，马上利用它们之间比的关系，无论数量是多少，都能快速得到另一个量。此时圆的面积和正方形的面积比都是一定的，不断地添加圆、添加正方形，它们都是按照一定的规律在变化的。这个“比”的出现，又让学生发现：“我还可以求到正方形面积与圆面积的比。”“我还可以求到阴影部分面积与圆面积的比。”……

建构主义认为，学生只有在自己原有认知结构的基础上学习和探索新知识，并将新知识与已有知识经验建立联系，形成知识的结构化，才能形成对知识的深刻理解。著名哲学家、儿童心理学家皮亚杰曾明确指出：“全部数学都可以按照结构的建构来考虑，而这种建构始终是完全开放的……这种结构或正在形成‘更强’的结构，或者在由‘更强’的结构来予以结构化。”新时代的教师应注重引导学生打通知识间的纵、横联系，学习知识，把握联系，灵活变通，让学生在已有知识结构上形成更强的、开放的知识结构，从而真正促进学生学习力的发展。

（作者单位：江西省南昌市育新学校红谷滩分校）