风洞洞壁干扰数值模拟研究
杨依峰,王锁柱,董 超,杨天鹏,苏 伟
(北京航天长征飞行器研究所,北京,100076)
0 引 言
风洞实验一直是航空航天飞行器设计、研制中重要的实验手段。虽然风洞的实验设计、流场品质和测量控制技术水平不断提高,数据的采集和处理方法不断完善,但是风洞洞壁干扰却一直伴随着风洞实验。
现阶段洞壁干扰的研究多采用壁压信息法,但是该方法却没有考虑洞壁边界层与模型之间的互相干扰。随着数值计算方法的发展和完善,许多新的流场模拟方法开始应用于风洞实验洞壁干扰问题的求解中。Mark Allan[1]通过求解RANS方程研究了风洞洞壁对绕三角翼流动的气动特性的影响,尤其是对涡破裂的影响。范召林[2]等人对跨声速风洞洞壁干扰数值模拟进行了初步研究。焦予秦[3]等人进行了机翼半模的洞壁干扰研究,通过求解N-S方程来数值模拟风洞流场,并进行风洞洞壁干扰的研究分析,但是其数值模拟结果与风洞实验值偏差相对较大。何瑞恒[4]通过求解N-S方程来进行旋翼模型洞壁干扰数值模拟,研究了风洞洞壁对旋翼流场干扰的影响。白井艳[5]通过数值仿真方法对风洞洞壁对翼型的影响进行了研究。然而他们仅仅对风洞实验段进行了数值模拟,并没有考虑风洞实验段入口处附面层的形状和厚度。
本文将风洞的稳定段、收缩段添加到数值模拟可以有效解决实验段入口附面层的问题。此外,本文针对风洞实验的特点发展了基于“风洞洞壁静压监测反馈调节系统”的数值模拟方法,通过该调节系统使风洞的数值模拟状态达到风洞实验的目标状态。并利用该数值方法对后掠机翼的风洞实验进行数值模拟,将其结果与自由来流状态下计算结果进行对比,研究并分析洞壁对风洞实验的干扰影响。
1 计算方法
采用Navier-Stokes方程作为流动控制方程,其积分形式为

式中V为控制体体积;为守恒变量矢量;Ω为控制体表面面积;为通过表面Ω的净通量矢量,包含粘性项和无粘项;n→为表面Ω的单位外法向矢量。
控制方程中的无粘通量项的离散采用AUSM (Advection Upstream Splitting Method)格式,时间离散方法采用LU-SGS隐式时间推进格式。湍流模型采用S-A湍流模型,此外本文采用了当地时间步长、隐式残值光顺、多重网格技术等方法来加速计算收敛。
2 实验模型及计算网格
2.1 实验模型
本文所选用的实验模型后掠角为20°,翼型为NACA0012-64的后掠机翼,机翼翼梢部分进行圆滑修正,使翼梢部位曲率光滑。该模型几何尺寸如图1所示,前缘后掠角为20°,机翼弦长c=0.1016 m,半展长翼展b/2=0.1524 m,展弦比AR=3,参考面积Sref/2=0.0155 m2。
实验采用的风洞为美国NASA Ames实验中心的高雷诺数固壁风洞[6],该实验风洞是直流暂冲式风洞。对于跨声速风洞实验,目前通常采用孔洞壁或槽壁以减小洞壁干扰。本文结合该固壁风洞实验结果研究基于“风洞洞壁静压监测反馈调节系统”的数值模拟方法,并研究固壁对跨声速实验的干扰影响。风洞实验段尺寸及实验模型安装如图2所示,风洞的截面形状为矩形,风洞上下壁有0.15°的扩张倾角,其目的是为了减小沿着风洞轴向附面层增长的影响。风洞的稳定段截面形状为圆形,收缩段从圆形过渡到矩形[7],其收缩面积比为37。
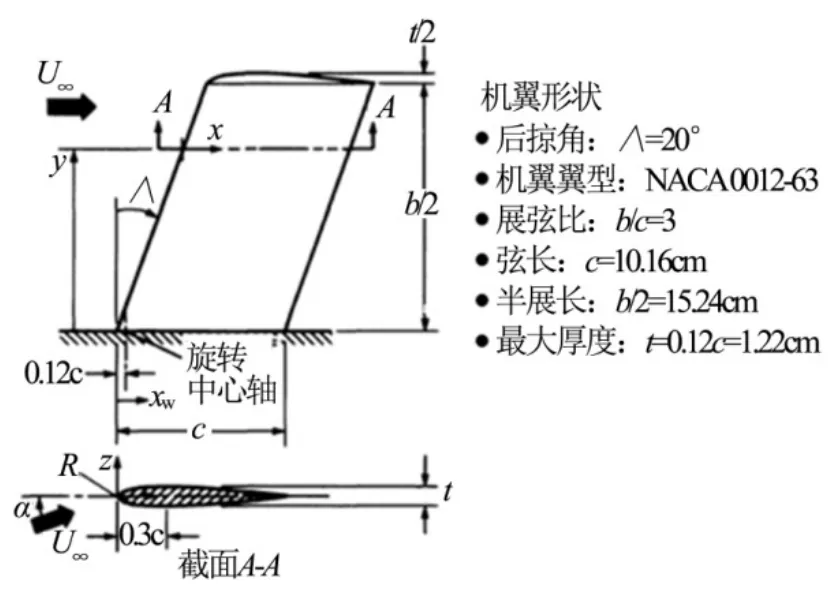
图1 机翼模型[6]Fig.1 Wing Model[6]
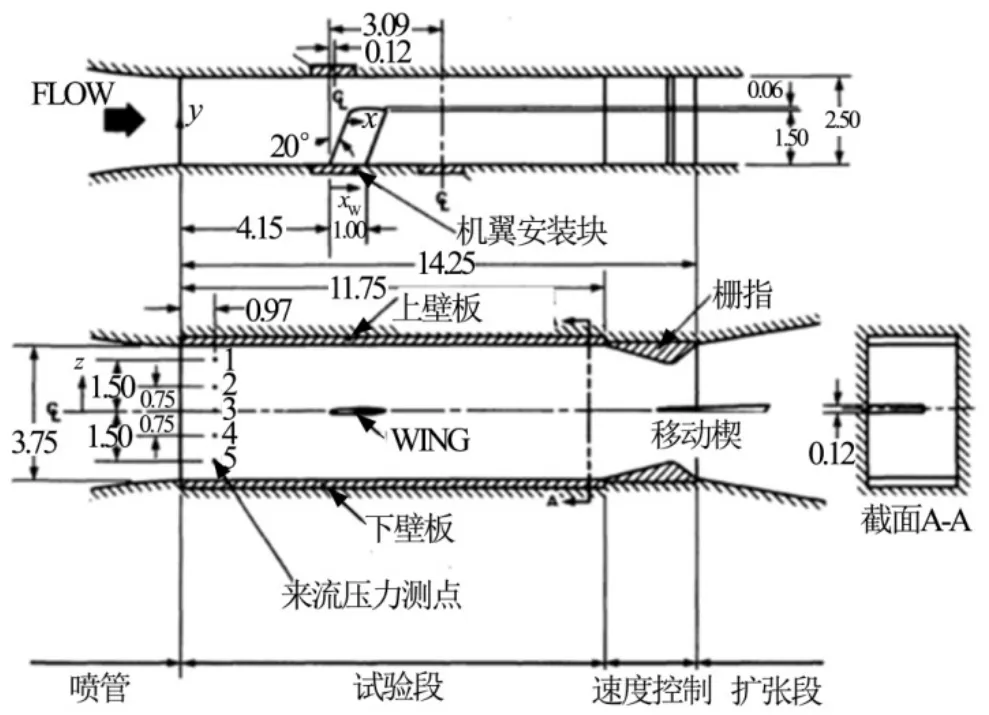
图2 风洞实验段模型Fig.2 Model of Wind Tunnel Test Section
原则上,风洞的数值模拟应当包括整个风洞,即风洞的稳定段、收缩段、实验段、扩张段、导流片、动力装置等。然而事实上,为了研究分析实验段的流动特性,模拟整个风洞是没有必要的,这样只会花费更多的时间和资源。如果仅仅模拟风洞实验段,实验段入口处的附面层形状厚度未知,将稳定段和收缩段添加到数值模拟中就可以解决附面层的问题,这是因为在稳定段前附面层会被去除。因此,对于风洞数值模拟只模拟稳定段、收缩段、实验段就已经足够了,同时,为了使风洞内流经机翼的流场充分发展,将风洞实验段延长,风洞几何建模如图3所示。

图3 风洞几何模型Fig.3 Geometry of Wind Tunnel Model
2.2 计算网格
由于需要模拟机翼在不同攻角下的风洞流场,则要根据不同攻角重新绘制CAD模型并重新生成网格。为了减小CAD建模及网格生成的工作量,本文采用嵌套网格技术,分别对机翼及风洞洞壁生成各自的面网格和体网格,然后将这两个网格合并在一起,通过两个网格的重叠区进行流场信息传递。
本文生成非结构混合网格,在物面生成三角形网格,并在物面网格基础上生成棱柱层网格,空间网格由四面体、金字塔形网格填充。对模型中的机翼前缘、翼梢等曲率变化大的部位及机翼与风洞的安装位置处进行网格加密。机翼翼面网格量为2.3万个,风洞洞壁物面网格量为6.5万个,起始棱柱层高度为0.001 mm(相对弦长1×10-5),棱柱层增长率为1.25,最大棱柱层层数为42层,网格总量450万个,所生成的网格如图4所示。
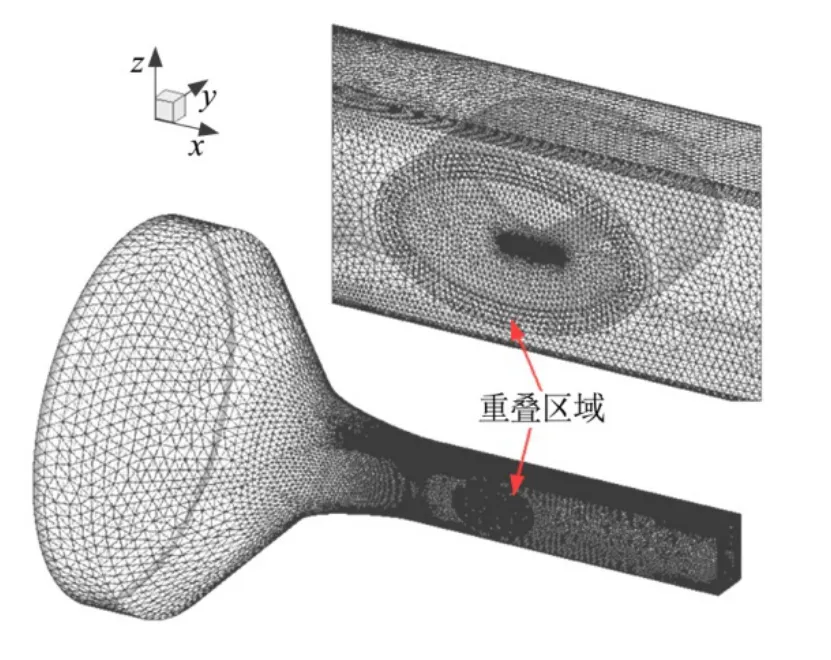
图4 风洞网格Fig.4 Computational Mesh of Wind Tunnel
图5为自由来流状态下的网格,其机翼物面网格分布与风洞模拟时机翼物面网格的分布相同,机翼附近的体网格分布大致相同,网格总量135万个。

图5 自由来流网格Fig.5 Computational Mesh of Wing in Free Air
3 反馈调节系统
3.1 风洞实验介绍
该实验风洞为直流暂冲式风洞,其实验总压、总温通过测量集气罐内的总压、总温得到,并且在实验开始前在风洞内安装皮托管,用其测量以确定风洞实验段的总压。为了减小皮托管对绕机翼流场的干扰影响,正式实验时没有皮托管。在机翼根部前3.18倍弦长位置处开有一个静压孔即静压监测点。由实验开始前测量得到的总压、总温,在监测点测得的监测点静压,通过等熵关系式和Sutherland公式可以得到实验的自由来流马赫数、雷诺数。
3.2 反馈调节系统的建立
本文对风洞流场进行数值模拟时,根据特征线理论设置边界条件。对于亚声速管道流动,入口边界条件为总压、总温,该边界条件是根据实验开始前的测量值确定的,出口边界条件为静压,该进出口边界条件满足特征线理论。调节出口压强,使风洞内压强监测点的压强与实验时测量值相同,即达到所要模拟的马赫数、雷诺数,该过程构成一个闭环反馈系统。建立如图6所示反馈调节系统。

图6 风洞洞壁静压监测反馈调节系统Fig.6 Feedback Control System of Monitoring Static Pressure on Wind Tunnel Wall
首先,读入网格并进行网格预处理,根据设定的边界条件进行流场求解,待求解迭代进行一定步数后,取得监测点压强,判断该压强是否与实验值相同。如果不同,调节出口压强,再进行流场求解,然后判断监测点压强是否与实验值相同。直到监测点压强与实验值相同且计算完全收敛,退出反馈调节过程,求解结束。
3.3 算例验证
采用上述所建立的反馈调节系统对风洞实验进行数值模拟,同时采用嵌套网格与非嵌套网格分别进行计算以验证嵌套网格技术的可靠性,计算状态为:Ma=0.825,α=0°,Re=8.08×106。
图7给出了相对机翼展长0.25及0.5站位处翼面压强系数分布并与风洞实验数据进行对比。从图7中可以看出采用该反馈调节系统的数值模拟结果与实验值吻合很好,具有较高的精度,能够很好地模拟风洞流场。此外,采用嵌套网格计算的结果与非嵌套网格计算所得到的结果一致,这说明采用嵌套网格技术模拟风洞实验是可行的。
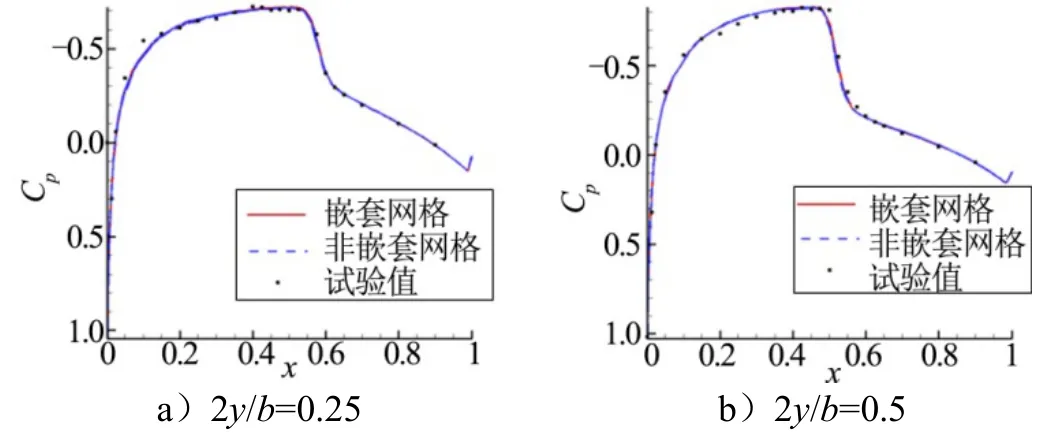
图7 压强系数曲线Fig.7 Computational Results Compared to Experiment Data
4 洞壁干扰研究
4.1 亚声速风洞洞壁干扰研究
将风洞流场的计算结果与自由来流情况下的流场进行对比,分析洞壁对绕机翼流动的干扰影响。亚声速风洞实验状态为:Ma=0.5,α=0°,Re=4×106。
图8为自由来流情况与风洞内流情况下相对机翼展长0.25及0.5站位处翼面压强系数曲线。从图8中可以看出,两种情况下机翼翼面压强分布大致相同。

图8 亚声速自由来流情况与风洞内流情况下的翼面压强系数对比Fig.8 Contrast Curve of Airfoil Pressure Coefficient between Subsonic Free Flow Conditions and Wind Tunnel Internal Flow Conditions
图9为带洞壁情况下与自由来流情况下的翼面压强差云图,从图9中可以看出,在机翼根部前缘压强变大,这主要是因为机翼安装在风洞侧壁,风洞侧壁边界层干扰导致的。在机翼其余位置翼面压强略微减小,这主要是由于机翼模型阻塞干扰效应引起的。对于该风洞实验,风洞洞壁限制了风洞内的流线向外偏移,因此,风洞流场中相邻流线之间的气流通道面积小于自由来流时的情况,这使得该机翼模型区域的平均气流速度高于模型远前方的来流速度。同时,风洞洞壁的边界层沿着气流方向逐渐变厚,这相当于减小了风洞实验段中的气流通道面积,气流速度沿着气流方向逐渐加速。因此,相比于无风洞洞壁的情况,风洞洞壁的存在造成了模型区域气流加速,压强减小。

图9 亚声速带洞壁情况下与自由来流情况下的翼面压强差云图Fig.9 Difference Contours of the Wing Pressure Coefficient between Flow with Wind Tunnel Wall and Free Flow at Subsonic Conditions
4.2 跨声速风洞洞壁干扰研究
跨声速状态:Ma=0.804,α=2°,Re=8×106。图10为跨声速自由来流情况与风洞内流情况下机翼翼面0.25及0.5展向站位压强系数曲线。从图10中可以看出,在跨声速状态下,流场的激波位置较自由来流情况下向后移动。图11为两种状态下的压强差云图,从图10中可以看出,在激波位置处压强变化特别明显,这主要是因为机翼激波位置对全局流场非常敏感。
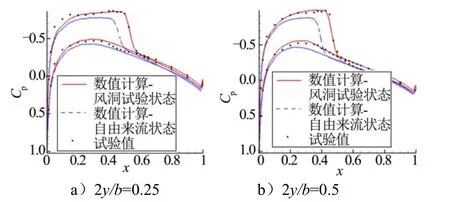
图10 跨声速自由来流情况与风洞内流情况下的翼面压强系数对比Fig.10 Contrast Curve of Airfoil Pressure Coefficient between Transonic Free Flow Conditions and Wind Tunnel Internal Flow Conditions
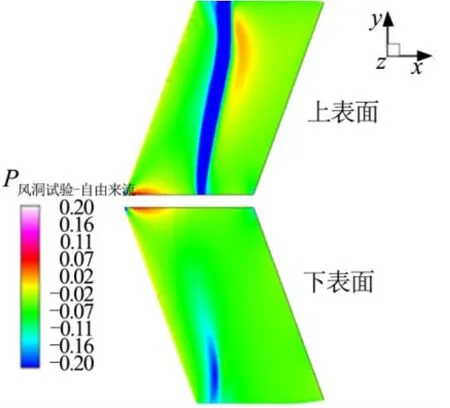
图11 跨声速带洞壁情况下与自由来流情况下的翼面压强差云图Fig.11 Difference Contours of the Wing Pressure Coefficient between Flow with Wind Tunnel Wall and Free Flow at Transonic Conditions
5 结 论
本文所研究的基于“风洞洞壁静压监测反馈调节系统”的数值模拟方法具有较高的精度,能够很好地模拟亚声速及跨声速风洞流场。
通过对亚声速和跨声速风洞实验进行数值模拟并与自由来流条件仿真结果进行对比发现:在亚声速情况下,风洞洞壁对流场的影响较小;而对于跨声速流动,相比于自由来流条件,风洞实验条件激波位置向后移动,且移动幅度较大,洞壁干扰影响较强。

