基于检测数据主成分分析的筒弹寿命评估预测模型

武 博，靳 冬，杨积东，陈闪闪，陈继勋

（1. 上海精密计量测试研究所，上海，201109；2. 中国合格评定国家认可中心，北京，100062）

0 引 言

导弹作为大型复杂武器系统，其性能、寿命的保持与恢复，对军队战斗力提升，乃至经济提升具有重大的现实意义[1]。近年来中国部分导弹武器装备面临陆续到达设计寿命末期，甚至已有装备超期服役的问题，准确掌握哪些装备可以继续服役、继续服役时间，及哪些装备需开展有效的维修以实现性能质量恢复，已成为军队装备保障工作的关键任务[2,3]。由于导弹武器系统具有“长期贮存、一次使用”的特点，必须实时监控筒弹的健康状况，才能在任务前期综合系统状态对筒弹的可靠性和寿命进行有效的评估和预测[4~6]。

目前寿命预测方法主要有基于物理模型的预测方法、基于经验的预测方法和基于数据驱动的预测方法[7~10]。其中基于物理模型的预测方法需要根据专家经验以及大量试验数据对研究对象建立数学模型，虽然准确性较高但成本也较高，因此，这种方法在应用上有很大的局限性；基于经验的预测方法只需知道对象的故障时间历史数据就可对筒弹寿命进行预测，但准确度不高；基于数据驱动的寿命预测方法通过数据挖掘的方式寻找数据中与故障相关的隐含规律并对未来数据进行预测，从而推断剩余寿命，无需知道对象的先验知识，适合具备大量监测数据的筒弹寿命预测。主成分分析（Principal Component Analysis，PCA）是一种正交变换，利用二阶的统计信息进行计算，其优势在于数据压缩以及对多维数据进行降维，能将具有一定相关性的多个指标重新组合成一组新的相互无关的综合指标进行替代，适用于评估指标涉及面广、不确定因素较多的质量分析和评估。

本文基于筒弹的测试数据，运用主成分分析法构建筒弹质量状态特征模型，基于质量状态特征模型建立寿命预测模型，对某型筒弹寿命进行评估预测分析，形成寿命预测曲线，实现对某型筒弹全寿命周期过程的健康评估。

1 质量状态特征模型

质量信息包括质量故障类型信息和质量故障程度信息，根据参数偏离状态人工挑选主参数，主参数组合反映故障类型、偏离状态大小反映故障程度。为了使模型有更好的普适性、更好的执行力，本项目使用主成分分析方法开发质量状态模型。PCA建模方法为

利用测试数据构建N维列向量表征筒弹：

一个批次M发筒弹形成的测试数据样本为

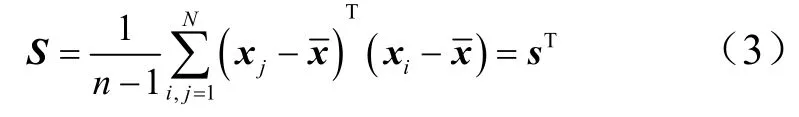
计算可得协方差矩阵S的特征值和特征向量：

式中

式中ΦS为向量矩阵，；ΩS为特征值矩阵。

根据累计贡献率确定主成分空间k：

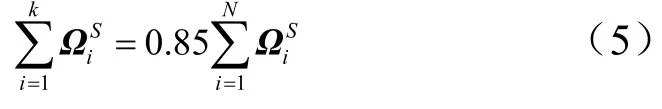
形成N×N的状态矩阵：

计算可得筒弹状态矩阵的特征值和特征向量：

式中ΦM为向量矩阵；ΩM为特征值矩阵。

根据特征值显著水平挑选前k个向量形成子空间，为一个N×k维矩阵，最后形成描述质量信息的k维数据向量：

若不考虑基于使用可靠性的直接缩维情况（即质量分析要素都有等概率发生故障的可能），因为PCA分解的信息维度有更好的正交性，相比于人工指定主参数组合，向量q的信息密度更高、状态程度评估会更加准确。

2 寿命预测评估模型

假设质量状态从优良到不合格是一个随确定性参数变化的连续过程（忽略故障隐患类型的影响），那么质量隐患程度q是一个连续函数。如果能事先得到质量状态足够丰富的产品样本，统计分析不同生命阶段中不同质量状态所对应的质量隐患程度q，就可以建立产品质量状态与质量隐患度量之间的关系。

寿命预测评估模型建模方法为：收集设计寿命期内批抽检、作训演习中“失败”、“合格”、“质优” 3种类型的产品测试数据，形成分析的标准数据集。利用质量隐患程度q度量不同“类型”产品在不同列装年数上的产品质量状态，建立如图1所示的质量状态判据。

图1 质量状态判据Fig.1 Quality State Criterion

列装年数超出寿命设计要求的产品统一按“预定寿命时刻”标尺进行质量状态判定。图1所示的质量状态判据模型可以根据数据积累每年更新。当数据量不足时，可以通过专家指定方式增加“合格”产品数量。

根据产品质量状态估算产品剩余寿命，如图2所示。通过产品检测数据可以得到质量状态特征度量q，经过影射1获得产品质量状态，再通过影射2获得产品剩余寿命。

图2 产品质量状态-剩余寿命关系 Fig.2 Quality State-residual Life

产品寿命预测可以分两种情况：在第1个寿命周期内；在第1个寿命周期外。图1中曲线1纵坐标点C1计算方法为

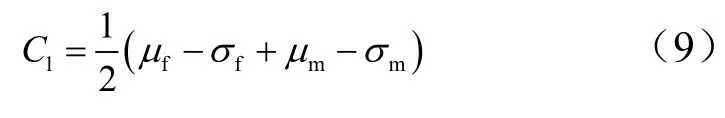
曲线2纵坐标点C2计算方法为

式中μf为失败产品的统计均值；μm为合格产品的统计均值；σf为失败产品的统计标准差；σm为合格产品的统计标准差。

3 某型筒弹寿命评估预测

考虑到程序实现的时效性、筒弹数据之间比较好的相关性和主成分分析的坐标变换特性，可以使用小样本数据进行分析。本文使用某型筒弹10组测试样本数据构建筒弹质量状态特征模型，其中前5组为合格数据，后5组为失败数据，基于质量状态特征模型建立寿命预测模型。

每个样本数据包含弹动信号、保险状态、速率陀螺和引爆脉冲等5个特征指标。经主成分分析后的质量状态空间如表1所示，降维为3个主成分，即根据85%特征值显著水平确定3个向量，形成10×3维度状态空间，对质量信息进行描述，进一步可以得到10个测试样本的质量隐患程度q，分别为0.557 795、 0.430 334、0.466 934、0.221 895、0.630 051、0.453 945、0.346 339、0.478 066、0.37 571、0.426 846。

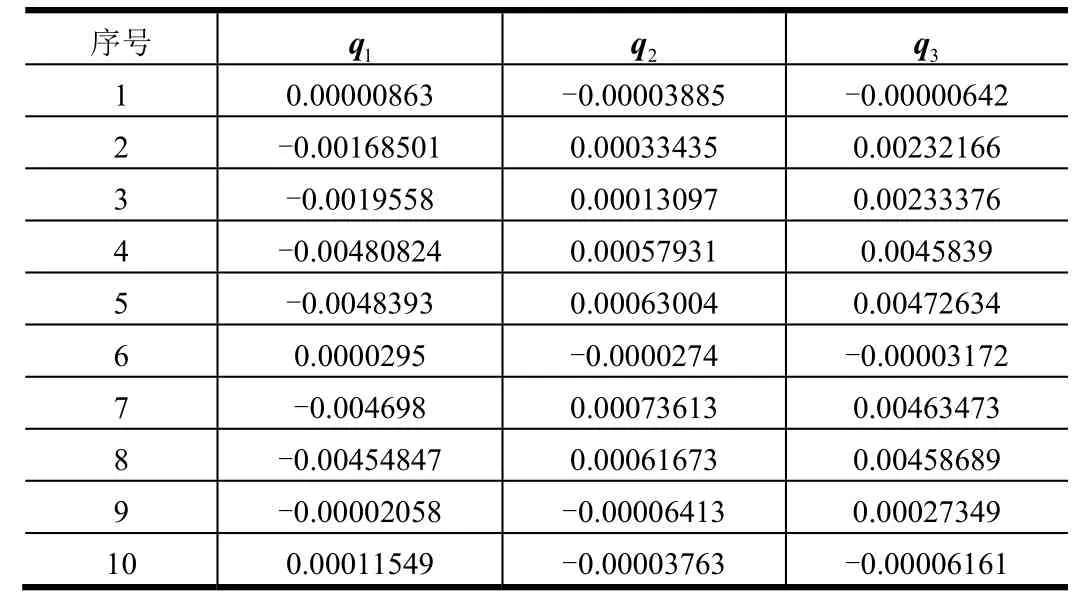
表1 质量状态空间信息表Tab.1 Quality Status Space Information

分别使用设计寿命期内列装年为1年、4年和8年的测试数据绘制图1中的两条质量判据曲线，失败产品及合格产品的统计均值和标准差如表2所示，根据式（9）和式（10）绘制如图3所示的质量状态判定曲线。

表2 统计均值和标准差数据表Tab.2 Mean and Standard Deviation Data

图3 质量状态判定曲线Fig.3 Flow Chart of Quality State Criterion

结合寿命预测模型和质量状态的类别判据对筒弹剩余寿命进行分析。当质量状态位于图1所示的“质优”区域内，产品剩余寿命等于设计寿命减去当前质量状态时间；质量状态位于图1所示的“失败”区域内，产品剩余寿命为0；产品状态位于图1所示的合格区域内，通过线性回归方法绘制寿命预测模型曲线。若该曲线与曲线1相交，则剩余寿命等于相交点所对应的时间减去当前质量状态时间；若与曲线1不相交，产品剩余寿命等于设计寿命减去当前质量状态时间。图4为对某型筒弹剩余寿命评估预测曲线，可以看出该筒弹设计寿命为10年，预测剩余使用寿命为1.5年。

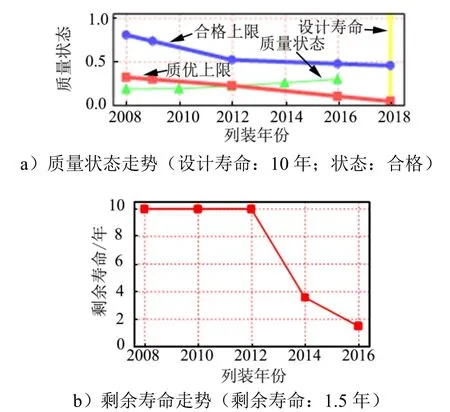
图4 某型筒弹寿命预测曲线Fig.4 Flow Chart of Certain Type Missile-in-container Life Prediction

4 结束语

本项目使用PCA建立筒弹质量状态特征模型和寿命预测模型，通过统计分析不同质量状态所对应的质量隐患程度，建立“合格”、“失败”和“质优”3个判据标尺，形成筒弹可靠性评估方法，绘制某型筒弹寿命预测曲线。基于数据的质量状态评估和寿命预测都是对历史经验的总结，在小批量情况下很难物理验证，主要从数据和算法两个层面进行综合验证，数据层面主要检查数据源范围是否覆盖了产品历史故障中的所有根事件，即所有根事件的状态信息在模型中是否都有参数变量描述；算法层面主要计算过程的精度，可以建立生命周期过程透明的验证数据集、通过过程反演进行预测验证。