考虑跨站停车的地铁客流协同控制模型

蒋琦玮，苏建凯，陈维亚

(1. 中南大学交通运输工程学院，轨道交通大数据湖南省重点实验室，湖南长沙 410075；2. 中南大学土木工程学院，湖南长沙 410075)

高峰时段城市轨道交通线路有限的运输能力与短时过饱和客流和客流分布不均衡相矛盾，易导致出现大客流车站乘客滞留集中效应突出与乘客等待时间过长现象，影响乘客乘车体验和列车与车站的运营安全[1]。为了解决城市轨道交通高峰时段客流过饱和与空间分布不均衡带来的问题，当前学者们主要针对车站客流控制、列车开行方案优化以及二者的协同优化3 种控制策略展开研究。在车站客流控制方面，赵鹏等[2]构建了线路层车站间与时间段协调控制模型，对线路运输能力、滞留率、滞留人次进行优化。XU 等[3]构建了以上车人数最大和乘客总延误时间最小的滚动优化限流控制模型。李登辉等[4]基于Fisher 最优分割法建模决策合理客流控制时段，优化了乘客候车等待时间。在列车开行方案优化方面，GAO等[5]建模优化了高峰时段列车跳停方案，以减少过饱和地铁线路中滞留乘客数量与乘客等待时间。NIU 等[6]基于高峰客流需求特征，建模并设计了遗传算法优化非均衡列车时刻表。戎亚萍等[7]构建高峰客流需求下的多编组列车开行方案设计模型，优化了乘客等待时间与企业运营成本。在客流控制与列车开行方案协同优化方面，JIANG 等[8]根据线路进出站乘客需求先确定列车跳停方案，再优化车站客流控制方案。LIU 等[9]基于拉格朗日松弛算法，优化求解站站停列车时刻表与客流控制策略。陈维亚等[10-11]从大小交路开行方案和快慢车开行方案与多车站限流方案进行协同优化，以减少乘客等待时间和均衡乘客需求。综上所述，在优化城市轨道交通高峰时段的运营策略时，不少研究开始注重将车站客流控制与列车开行方案协同考虑，研究重点主要是寻求开行方案中的某个要素与车站限流的组合优化策略。考虑多数文献以固定客流需求为假设且先优化开行方案后优化车站限流方案，本文针对城市轨道交通高峰期客流需求时变且不均衡特征，分析构建列车跨站运营与多车站客流协同控制的同步优化模型和算法，优化车站乘客滞留率和乘客候车等待时间。

1 问题描述

1.1 问题界定

针对1 条城市轨道交通线路，如图1所示，共有S座车站，某高峰时段T内有K列列车按照一定开行间隔依次从车站1 运行至车站S，运行列车可采取站站停或跨站停开行方案，其中跨站停列车在部分车站不停车通过。高峰时段的客流需求超出线路运输能力，部分车站出现客流滞留现象，根据需要在若干车站采取进站客流限流控制策略。

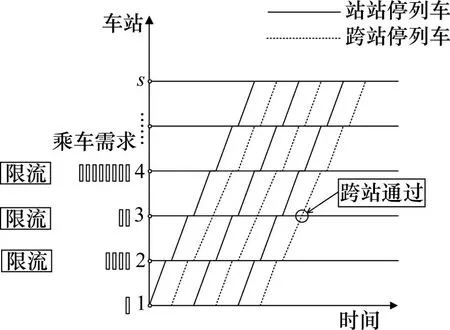
图1 停站与限流协同控制示意图Fig.1 Schematic diagram of coordinated control of station stopping and current limiting

本文研究的问题是：针对具有上述运营特征的线路，需要按照某种优化目标决策确定跨站停列车及跨站方案，同时确定限流车站及进站限流人数的比例。

1.2 问题假设

根据城市轨道交通列车开行方案与车站客流需求的特点，本文提出以下假设：

1) 线路采取单一交路，跨站停列车与站站停列车车型、编组相同。

2)线路OD 客流需求随时间变化，在同一时间段内相对稳定。

3) 乘客的进站、乘车等行为遵循“先到先服务”原则。

4) 线路不具备越行条件，跨站停列车与站站停列车在通过车站时，列车追踪间隔保持不变。

2 数学模型

为了更好地表达模型，先定义ST={1,2,3,…,S}为车站集合，车站具有属性ys，表示车站是否可不停车通过，可跨站通过时取0，不可跨站通过时取1；TR={1,2,3,…,K}为列车集合，列车具有属性xk，表征列车是否跨站停，跨站停取1，站站停取0；为使模型能获得较好的车站客流控制策略，将优化时段T拆分成若干客流控制时段，控制时段集合为TN={1,2,3,…,N}，时间粒度为Δt=T/N。

2.1 客流推演

2.1.1 到站乘客数量

车站每个控制时段累计乘客数量，包括该时段到站乘客与上一阶段站外滞留乘客，设置各站在控制时段内的进站限流率，限流率与累计乘客数量的乘积即为被限制在站外无法进站的乘客数量。故车站s在控制时段n内累计乘客数量为

2.1.2 进站乘客数量

车站s在控制时段n内进站的乘客数量由车站累计乘客数量和车站限流率决定。列车k与前次列车发车间隔内的进站乘客数量由列车到站时间与控制时段的关系确定。通过式(3)将与控制时间相关的进站乘客数量转换为与各次列车到站时间相关的进站乘客数量。

2.1.3 站台乘客数量

列车k与前次列车发车间隔内，站台乘客数量变化由站台滞留乘客数量与进站乘客数量决定。站台乘客的上车需求，结合列车k的停站方案确定，乘客根据列车k经停的车站确定是否选择搭乘列车k。故在列车k到达车站s时站台乘客数量为

2.1.4 列车乘客数量

列车k经停车站s时与站台乘客发生上下车交互关系，车站s的上车需求与列车k的剩余乘客容量决定了实际的上车乘客数量。

2.2 目标函数

相关研究主要以乘客出行时间或等待时间最小为优化目标，较少考虑到车站乘客滞留集中效应突出，即不同车站间乘客滞留比例差异过大的问题[11]。本文选取乘客车站乘客滞留率方差最小与乘客在站等待时间最小为优化目标。

2.2.1 车站乘客滞留率方差和最小

车站乘客滞留率用站台乘客和站外乘客滞留人次与该站总乘客数量的比值来表示，即为该站人均滞留次数。根据各站乘客滞留率得到乘客滞留率方差，滞留率方差的大小反映车站乘客滞留集中效应的强度，线路车站乘客滞留集中效应的强度与各站乘客滞留率方差的大小成正比。

2.2.2 乘客在站等待时间最小

乘客在站等待时间包括站台等待时间和站外等待时间，其中乘客站外等待时间式(10)与车站和优化时段相关，乘客站台等待时间式(11)与车站和车次相关。

式中：Z1表示乘客站外等待时间和；Z2表示乘客站台等待时间和；Δtd表示列车发车间隔。

2.3 约束条件

2.3.1 列车与站台安全容量约束

式(13)为站台容量限制，式(14)为列车容量限制。

式中：Cp s表示站台s的安全容量；Ctr表示单列列车的安全容量。

2.3.2 列车追踪间隔约束

列车在线路运行过程中，前后列车在同一车站的到发时间需满足最小列车追踪间隔。

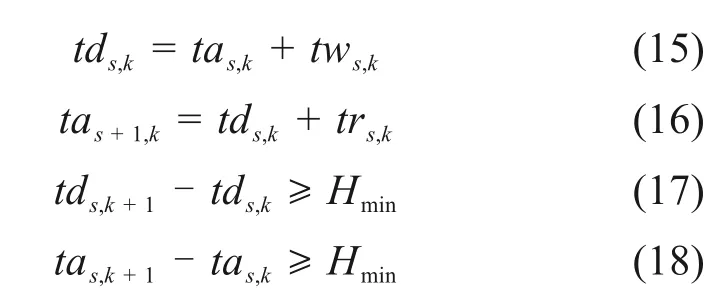
式中：tds,k表示列车k离开车站s的时间；tas,k表示列车k到达车站s的时间；tws,k表示列车k停留车站s的时间；trs,k表示列车k从车站s到s+1 站的运行时间；Hmin表示线路的列车最小追踪间隔。

2.3.3 跨站停列车跨站数量约束

式(19)为单次跨站停列车的最大跨站数量限制。

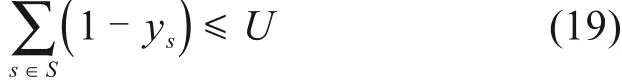
式中：U表示单次跨站停列车的最大跨站数量。

2.3.4 列车发车频率约束

式(20)为列车发车频率约束，站站停列车与跨站停列车的发车频率之和受线路运营条件和列车保有量限制。

式中：f1表示站站停列车的发车频率；f2表示跨站停列车的发车频率；fm表示总的列车发车频率。

3 算法求解

考虑跨站停车的地铁高峰时段多站客流协同控制模型为双目标MINP 非线性混合整数规划模型，由于列车停站方案及车站客流控制的相互影响，无法直接进行求解。目标函数M1以各站乘车需求滞留率方差最小化为中心，目标函数M2以乘客等待时间最小化为中心，两目标函数缺少共同量纲，对原目标函数进行“min-max 标准化”处理[12]得到M′1和M′2，采用线性加权法[13]，将两目标函数缩放，制定权重叠加得到单目标函数。

式中：w1，w2为权重系数，其中0 ≤wi≤1，w1+w2= 1；M′1，M′2为对应函数线性变化后得到的标准化函数。

差分进化算法是一种依据种群个体差异信息决定搜索方向的进化算法。对模型中多约束非线性规划的单目标函数问题，使用改进的自适应差分进化算法(DE)进行求解，在基本差分进化算法中设计自适应缩放算子和交叉算子以改进算法性能[14]。式(23)为改进的缩放算子，式(24)为改进的交叉算子。

基本差分进化算法中，缩放算子取常数，常数过高易导致全局最优解降低，群体多样性下降出现“早熟”现象。在缩放算子中引入参数λ，使缩放算子初期为2F0，保持种群多样性以避免早熟，后期缩放算子逐渐降低至F0，避免最优解遭到破坏。引入随机范围的交叉算子，使交叉算子在0.75 附近动态变化，在保证算法效率同时，提高种群多样性。

模型算法流程如下所示。

Step 1：确定差分进化算法控制参数，确定适应度函数。算法控制参数包括：迭代次数Gm，种群大小NP，缩放算子F与交叉算子CR。

Step 2：随机产生初始种群，种群个体由列车停站方案与车站限流方案组成，采用二进制编码与浮点数编码，编码长度为S+S*N，其中车站限流方案满足约束(13)和(14)，停站方案满足约束(19)。

Step 3：种群内进行变异、交叉、选择操作，对新得到的个体进行筛选，舍弃不符合约束条件的个体，并重新生成新个体。

Step 4：对种群进行评价，计算初始种群中每个个体的适应度值，经线性加权后的目标函数式(21)作为适应度函数。

Step 5：判断是否达到终止条件，若是，则终止进化迭代，将得到最佳个体作为最优解输出；若否，继续。

Step 6：在原种群和中间种群中选择个体，得到新一代种群。

Step 7：进化代数g=g+1，转Step 3。

4 算例分析

4.1 数据输入

某条城市轨道交通线路车站数10 座，平均站间距2.36 km。列车运行速度45 km/h，列车停站时间30 s，列车起停附加时间15 s，列车最小追踪间隔150 s。单次列车定员Ctr=1 440 人。线路发车间隔Δtd=150 s，线路发车能力每小时24 列，站站停列车与跨站停列车开行频率f1:f2=2:1[8]。车站客流控制时段划分的时间粒度取Δt=10 min，单次列车最大跨站数量U=2，车站进站客流最大限流率αmax=50%[2]，目标函数中权重系数w1，w2,分别取0.6，0.4。

研究时间时段为早高峰7:30～8:30，仅考虑上行方向，线路高峰时段的时变到站乘客需求如图2所示，各站客流去向比例如表1所示，可见高峰时段线路客流分布在时间和空间上严重不平衡。车站客流分布不均表现在车站4 和5 客流需求较大，且线路各站客流需求随时间变化明显。高峰时段的这种客流时空特性，易导致车站4，5，6出现乘客大量滞留现象。

图2 线路早高峰时段车站乘客到达人数Fig.2 Number of passengers arriving at the station in early peak hours

表1 各站到达客流去向比例Table 1 Destination rate for arrival passengers

4.2 结果分析

设置自适应差分进化算法迭代次数Gm=300，种群大小NP=100，初始缩放算子F0=0.4，交叉算子由式(24)确定，应用Matlab R2018a 执行自适应差分进化算法，目标函数在迭代200次左右收敛。

在预设条件下，得到最优解目标函数值0.222 8，最优解列车开行方案为线路每小时开行16列站站停列车和8列跨站停列车，跨站停列车在第3站不停车通过，生成车站限流方案在2，3，4，5，6等5个车站进行车站协同限流，对应车站各时段进站客流控制率如表2所示。

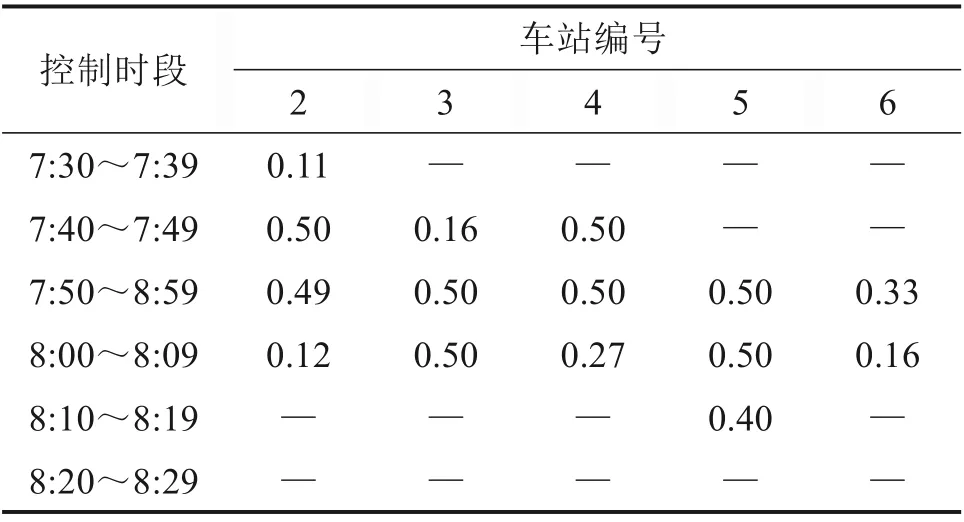
表2 进站客流控制率Table 2 Control rate of inbound passenger flow

在考虑跨站停车的城市轨道交通客流协同控制模型优化下，选取6个性能指标进行对比，结果如表3所示。与优化前相比，线路运输乘客数量提高0.66%，乘客周转量降低1.71%，乘客站台候车时间减少26.49%，乘客站外候车时间减少21.86%，乘客总候车时间减少24.78%。各站滞留率方差减少60.23%。协同控制后，乘客周转量有小幅下降，但乘客总等待时间大幅度减少，服务质量得到较大提升。优化后乘客周转量下降的特征与文献[4]的研究相吻合。乘客周转量小幅下降与运输乘客数量的小幅上升，表明协同控制优化后，系统更多的满足了短途出行乘客的乘车需求。

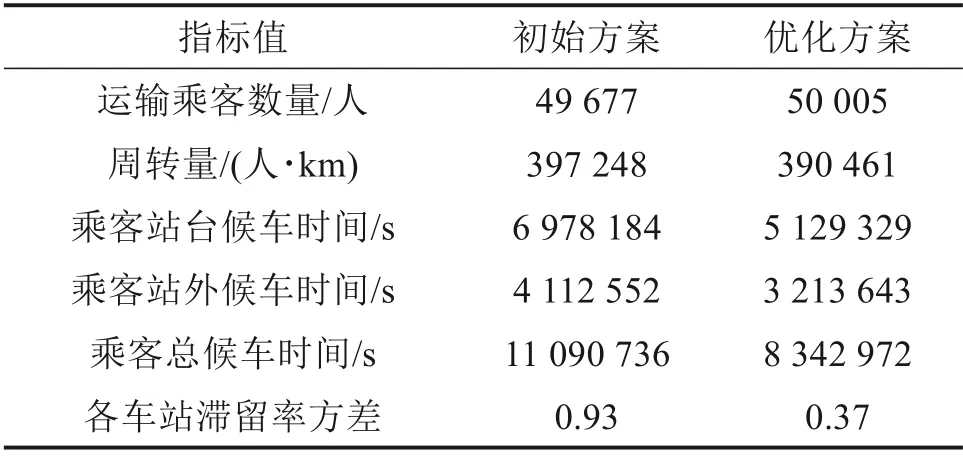
表3 优化方案性能指标Table 3 Index values of optimization scheme

优化前后各车站滞留人次与人均滞留次数如如图3 所示，优化后的车站滞留率方差减少60.23%的效果，体现在车站的滞留人数在线路车站维度上变化更加平缓，滞留集中效应有所缓解，以及各站人均滞留次数的变化更加平缓，高峰时段的乘客出行需求，不同车站的乘客可以获得更加均衡的乘车机会。

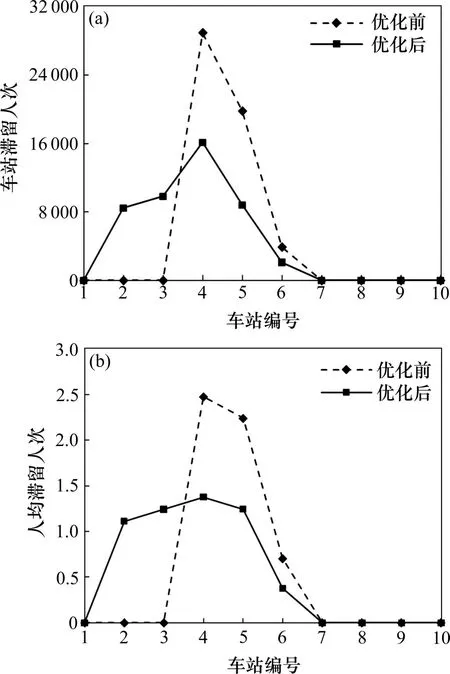
图3 各车站滞留人数Fig.3 Number of people stranded at stations

车站4 和5 在协同优化前是线路中出现乘客严重滞留的车站，由图4 车站站台时变人数可以看出，优化前车站4 站台人数达到饱和后持续到8:10分后开始下降，车站5站台人数达到饱和后维持在饱和状态。协同控制优化后，2 车站站台人数在随时间波动中始终未达到饱和状态。从协同控制优化车站站台人数前后的对比，可以看出优化后站台乘客密度显著降低，有效提升站台乘客候车安全性。

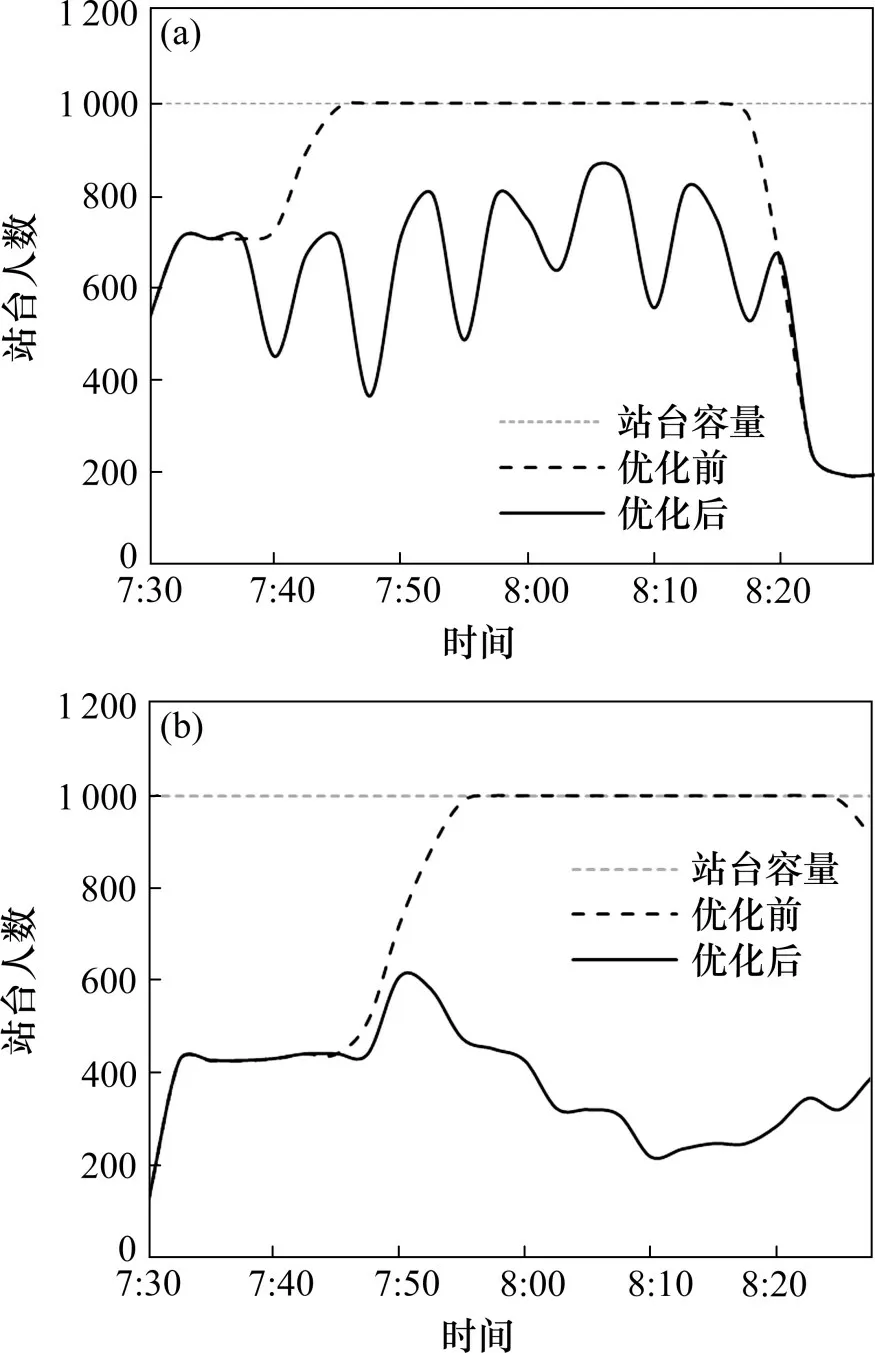
图4 车站站台时变人数Fig.4 Time varying aggregation number of station platform

考虑跨站停车的地铁客流协同控制模型中，2个目标函数采取线性加权方式进行处理，w1，w2的取值会对最终结果产生较大影响，由图5权重系数取值对目标函数的影响可以看出目标函数与权重系数间的变化趋势，乘客总候车时间与w1取值呈正相关，车站乘客滞留率方差与w1取值呈负相关。w1取值由0.1 变化至0.3 时，乘客总候车时间下降速度较快；w1取值由0.7 变化至0.8 时，车站滞留率方差增加速度较快。在实际运营决策中，建议w1取值在0.3 至0.7 之间，以保证较好的双目标优化效果。

图5 权重系数取值对目标函数的影响Fig.5 Influence of weight coefficient on objective function

5 结论

1) 构建考虑列车跨站运营的多站客流协同控制模型，在高峰时段客流需求时空特性的基础上，以车站滞留率方差最小与乘客候车等待时间最小为双优化目标，设计自适应差分进化算法求解。算例表明提出的模型和算法能较好地求解出列车停站与车站限流协同控制方案，有效降低车站滞留集中效应与减少乘客候车时间。

2) 模型实例验证结果中乘客候车时间大幅降低的同时，出现线路乘客周转量降低1.86%，从该角度造成了系统运输能力小幅下降，此现象在其他论文中也出现类似结果。在后续研究中将考虑分析提升高峰时段城市轨道交通线路运营效果的各优化指标间的相互影响关系。