基于混沌粒子群的改进LEACH算法

刘晓理，王出航，王 雪

(长春师范大学 计算机科学与技术学院，吉林 长春 130012)

0 引 言

无线传感器网络(Wireless Sensor Networks，WSNs)是由大量廉价的微型传感器节点组成的[1]。由于WSNs具有传感、计算、数据处理和通信能力等特点[2]，逐渐被广泛应用于需要感知和监测数据的各个领域，如军事战争、工农业生产和智能家居等多个领域。

无线传感器中节点自身能量有限且不易补充，使其在功率、存储以及计算过程方面受到诸多限制[3]。因此，如何最大程度地降低网络能耗成为WSNs路由协议设计中最具挑战的问题之一。LEACH算法因具有能量利用率高的特点被广泛应用于路由协议设计中[4-5]，其运行过程分为簇的建立和数据传输[6]。但LEACH算法仅是通过随机概率的方式产生簇头，并未考虑到节点能耗的差异性[7]。针对此问题，文献[8]通过计算每个节点的中心度和邻居数解决了选择簇头节点产生的随机性。文献[9]提出的粒子群算法虽然优化了簇头选择，但没有考虑到粒子群算法易陷入局部极值的问题。

针对LEACH算法中随机概率选择簇头所产生的能耗问题和粒子群算法自身所存在的缺陷问题，文中提出一种基于混沌粒子群的LEACH算法(CPSOLEACH)，该算法基于混沌粒子群算法优化簇头选择，同时引入混沌序列，增加粒子群的多样性，这样既能提高能量效率，均衡节点之间消耗，减少盲节点出现，也能避免粒子群算法陷入局部最优。

1 系统模型

1.1 网络模型

文中研究的网络模型是在M×M区域内随机部署N个传感器节点，基站位于区域内的中心位置，具体设定条件如下[10]：

1)网络部署完成后，包括基站在内的所有节点都不可移动;

2)同构节点被认为具有相同的传感、处理、存储、通信能力和初始能量;

3)基站在能量、处理、通信能力等方面没有限制，可以与网络中的所有节点进行通信;

4)任意两个节点之间的无线传输链路是完全对称的，因此，对于两个节点之间相同数量的数据传输能耗是相同的;

5)任意两个节点之间的距离可以通过接收到的信号强度来获得。

1.2 能量模型

在LEACH算法中，采用与文献[10]相同的能量模型，即一阶无线电模型。具体计算为

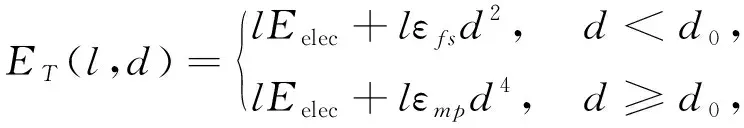
(1)

式中：Eelec——发送或接收数据所消耗的能量;

εfs、εmp——分别表示处于自由空间模型和多径衰落信道模型时的功率放大所需要的能量系数；

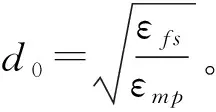
当发送距离d小于距离阈值d0时，采用自由空间模型，反之，则采用多径衰落信道[11]。

2 算法设计

2.1 混沌粒子群算法

基本粒子群算法是一种模拟自然界中鸟群觅食行为的随机优化算法，每个粒子都可以看作是一个解[12]。每个粒子的适应度值是由给出的适应度函数计算而来，从而得知每个粒子的个体极值和全局极值。粒子会根据个体极值和全局极值不断更新粒子的速度和位置，如下式

混沌是一种具有内在规律性的非线性随机运动形式，具有对初始条件极端敏感性、遍历性和类随机性的特点[13]，在较长时间内混沌可以不重复地遍历相空间中的各个点[14]，因此在粒子群算法中引用混沌思想有助于算法保持群体的多样性，扩大种群搜索范围，跳出局部最优。经过验证，Tent映射比Logistic更能产生分布较均匀的初始值，具有更好的均匀遍历性[15]，文中采用Tent映射的方式产生混沌序列，

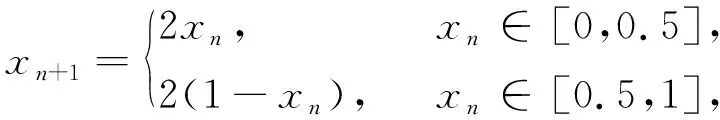
(3)

其中，xn∈[0,1],n=1,2,3,…。

2.2 基于混沌粒子群的LEACH算法

CPSOLEACH算法通过改进的粒子迭代公式，寻找能量较多且与基站距离较近的节点作为簇头，具体流程如下：

1)初始化相关参数，包括粒子群算法中的个体学习因子值c1、群体学习因子值c2、惯性权值w、粒子群种群规模n、粒子维数d(也就是网络中节点的个数)、最大迭代次数Tmax、粒子飞行速度的上限vmax和下限vmin。

2)预分簇阶段，初始化粒子群，即随机生成N×D的01矩阵，其中1为簇头，0为普通节点，确定最优簇头数为K[14]，

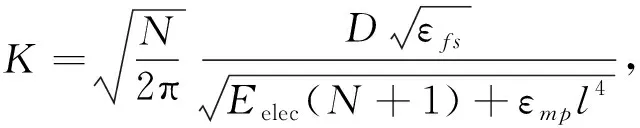
(4)

式中：N——网络中存活的节点个数；

D——网络区域的长度；

l——簇头节点到基站之间的距离[14]。

3)计算簇头的适应度函数值fitnessi，适应度公式为

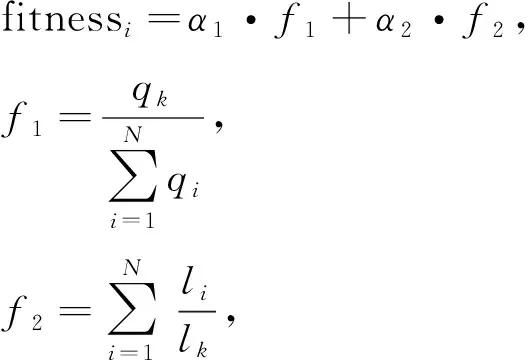
(5)

式中：f1——能量评价因子，表示簇头的剩余能量与网络中所有节点的剩余能量总和之比；

qk——第k个竞选簇头的剩余能量；

qi——网络中第i个节点的剩余能量；

f2——距离评价因子，表示网络中所有节点与基站的距离之和与此时当选的簇头与基站的距离之比；

li——网络中第i个节点与基站之间的距离；

lk——第k个簇头与基站之间的距离；

α、β——均为影响因子,满足α+β=1。

从式(5)可以看出，网络中的节点拥有剩余能量越多，并且与基站之间的距离越近，适应度值越大，其当选为簇头节点的概率越高。

4)根据文中新适应度函数公式更新个体极值pbest和全局极值gbest，并根据式(2)更新粒子的位置和速度，根据式(3)对粒子序列进行混沌优化。

5)迭代次数加1，回到3)，直至达到最大迭代次数，输出全局极值，最优粒子极值即最优簇头。

3 仿真分析

采用Matlab仿真平台，模拟网络区域为100 m×100 m的正方形区域，基站位于区域中心(50，50)，随机部署网络节点，其分布模型如图1所示。

图1 网络节点部署示意图

为了验证CPSOLEACH算法的有效性，从能量消耗总和、存活节点数和网络剩余能量3个方面对LEACH、LEACH-E和CPSOLEACH算法进行对比分析，分别如图2和图3所示。

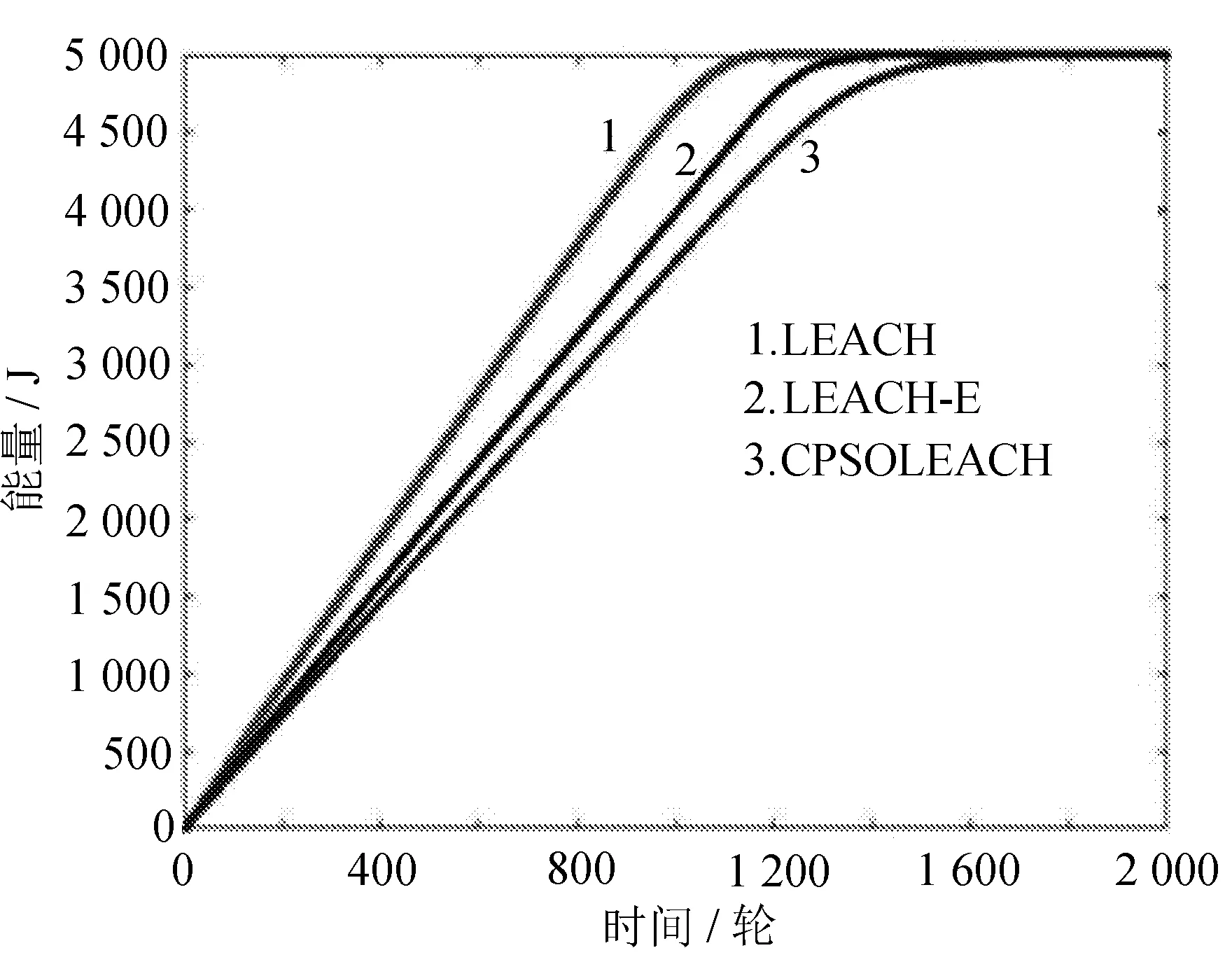
图2 能量消耗总和对比

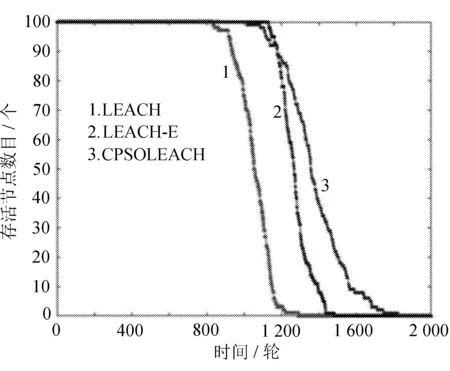
图3 存活节点数目对比

由图2可见，LEACH算法和LEACH-E算法分别在第1 253轮和1 467轮时能量就已经全部消耗完毕，而CPSOLEACH算法在第1 781轮时能量才全部消耗完毕。

由图3可见，LEACH、LEACH-E算法在第1 253轮和1 466轮时区域内的节点就已经全部死亡，而CPSOLEACH算法是在第1 781轮时区域内的节点才全部死亡。

网络剩余能量对比如图4所示。

图4显示了3种算法在能量均衡方面的性能，CPSOLEACH算法中的网络剩余能量一直都比LEACH和LEACH-E高。

从上述几个方面可知，CPSOLEACH算法能够有效节省能量，延长网络生命周期，这是因为CPSOLEACH算法采用混沌粒子群算法优化了簇头选择，均衡了网络能量。

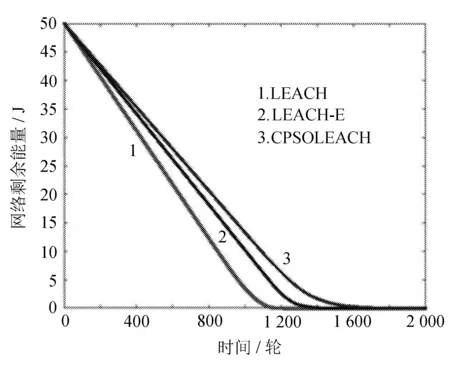
图4 网络剩余能量对比

4 结 语

在传统LEACH和粒子群算法的基础上，提出CPSOLEACH算法。结合LEACH算法给出含有节点能量因素和与基站距离因素的适应度函数，并运用新的适应度函数进行迭代选取最优簇头，即剩余能量多和与基站距离较近的节点当选簇头。同时，在搜索簇头的过程中，采用Tent混沌映射优化粒子群算法，扩大了簇头的搜索范围，也避免了粒子群算法后期陷入局部最优。通过Matlab仿真分析，证明了CPSOLEACH算法可以降低节点和网络能量消耗，延长网络生命周期。