基于时步有限元的车用座椅电机异常阶次噪声研究*

邓世奇 丁渭平 吴昱东 朱斐翔 韩佳慧

（1.西南交通大学，成都 610031；2.延锋安道拓座椅有限公司，上海 201315）

主题词：永磁直流电机 阶次噪声 非对称辅助槽 时步有限元 不平衡磁拉力

1 前言

永磁直流电机由于成本低廉、结构简单、性能可靠等诸多优点被广泛应用，而随着技术的发展和人们生活品质的提高，消费者对电机噪声的要求愈发严格和挑剔[1]，这对电机噪声控制提出了新的挑战。目前，关于电机本体噪声的治理方案主要集中于优化主阶次电磁力幅值以降低定子壳体的振动响应[2-7]。然而，直流电机往往存在异常阶次噪声，即声振频谱中主阶次不为槽数的整数倍，这类问题由于其成因的多样性、复杂性通常更难解决。为满足对直流电机日益严苛的噪声要求，提高车用电动座椅的乘坐舒适性，有必要对电机的异常噪声问题进行深入的研究与分析。

本文首先对气隙磁场、电磁力波产生机理及其特征进行深入分析，在此基础上，借助时步有限元方法计算电磁力，并将其映射至电机壳体结构以分析结构振动响应特征，以在此过程中判明异常阶次噪声产生的根源，最后从工程应用角度出发，提出相应的优化方案，以解决异常阶次噪声问题，提升电动座椅的乘坐舒适性。

2 问题的提出

直流电机安装在座椅的不同位置，可分别升降座椅的垂直高度、调整座椅前后位置和倾斜度，座椅的乘坐舒适性与电机运行时的噪声密切相关。本文的研究对象为某4极10槽永磁直流有刷电机，为车用座椅的升降电机，其内部结构如图1所示，实物如图2所示，基本参数如表1所示。

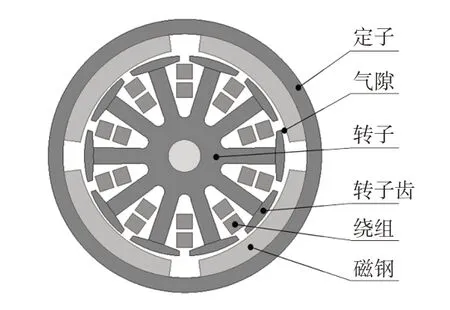
图1 永磁直流有刷电机结构示意

图2 车用座椅升降电机

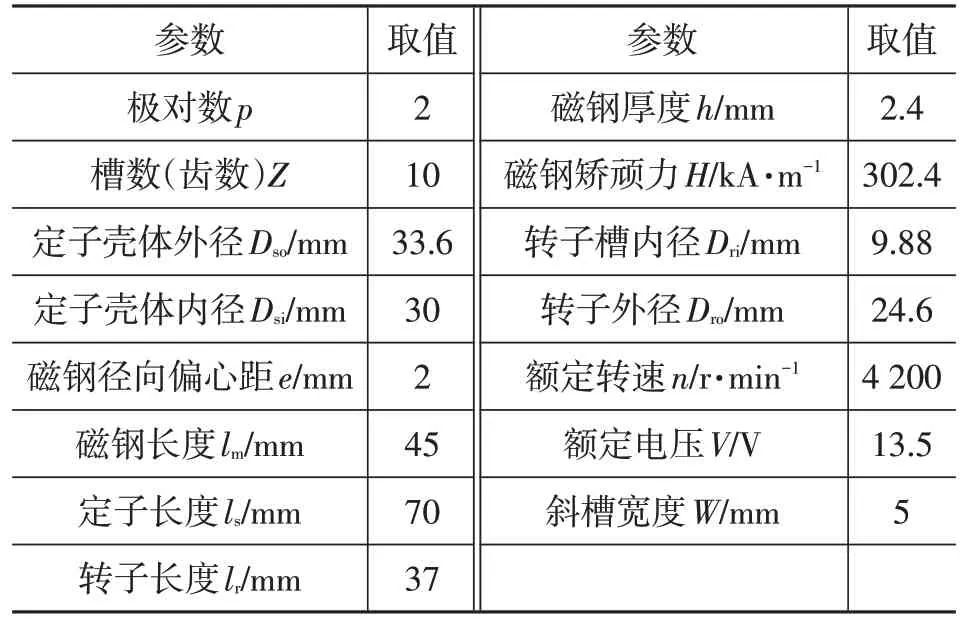
表1 直流电机的基本参数

如图1 所示，电机转子在旋转过程中，转子齿与磁钢会产生相互作用的电磁力，转子齿每次进出极靴，其与磁钢内表面的间距，即气隙长度会发生变化，从而产生电磁力的波动，其中作用在磁钢内表面的径向电磁力波是电机振动噪声的主要来源，因此转子齿槽与磁钢的数量、尺寸和气隙等参数是影响电磁力特征的重要因素。理想情况下，该4极10槽电机的噪声阶次应是齿槽数的整数倍，即主阶次应是10 阶及其谐波阶次。但应用中发现，某批次直流电机均出现异常阶次噪声的现象：在恒转速工况和升速工况下，该电机噪声幅值最高的阶次为11阶，其次是20阶，如图3所示。此时作为突出的异常阶次，11 阶次的噪声对电机整体噪声贡献较高，将严重破坏座椅的乘坐舒适性，进而影响整车的NVH性能。因此，对11阶噪声必须引起足够的重视。

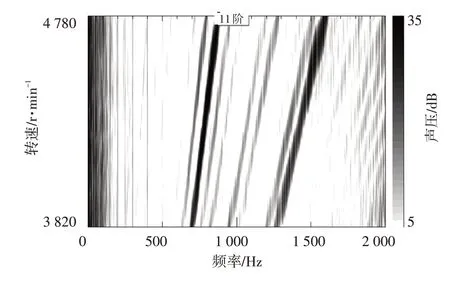
图3 升速工况下的电机噪声试验结果

3 机理分析

电机作为一种典型的旋转机械，引起其异常阶次噪声的原因有很多，如轴承问题、减速器齿轮配合问题、电机冷却风扇噪声、电磁力激起定子壳体结构模态产生共振、电机自身产生了不平衡磁拉力等[8]。本文异常阶次噪声信号是直接测量电机单体噪声所得，因此可以直接排除轴承和减速器的影响；该电机无冷却风扇，故可排除冷却风扇的影响；图3 表明，11 阶次特征明显跟随电机转速变化，因此可进一步排除定子壳体结构模态的影响。综上，该电机噪声的异常阶次可能与电机内部的旋转件有关，即电机在一个旋转周期内产生了异常阶次的电磁力作用在定子壳体上，从而产生异常阶次的噪声。

3.1 气隙磁场分析

忽略磁路饱和效应，电机气隙磁场满足[9]：

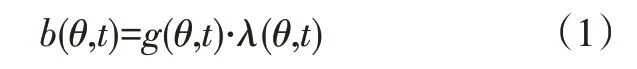
式中，b为气隙磁通密度；g为气隙磁动势；λ为气隙磁导；θ为空间角；t为时间。

进一步，对气隙磁导λ，有[10]：

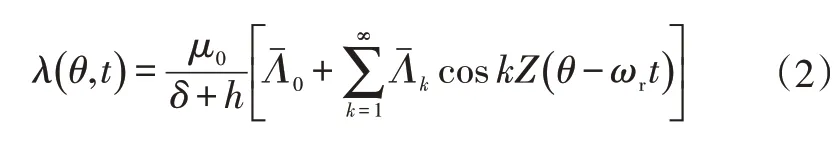
式中，μ0为空气磁导率，为常数；δ为气隙长度；h为磁钢厚度；Z为转子槽数（齿数）；ωr为转子旋转的角速度；为卡特系数。

将式（2）代入式（1），并令Bδ=μ0Hh/(δ+h)，则气隙磁通密度可写成：

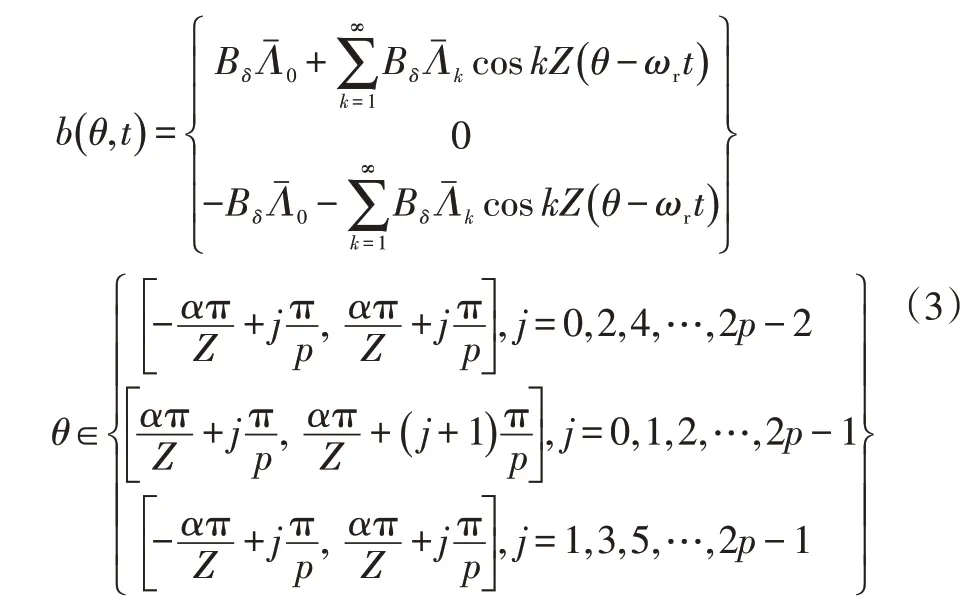
式中，α为1个极靴所对应的转子槽数量。

3.2 径向电磁力阶次分析

由于本文的研究对象是圆筒形电机，切向电磁力对圆筒形电机噪声贡献较小，故仅考虑径向电磁力。根据麦克斯韦应力张量法可得单个磁钢表面的径向电磁力密度[11]：

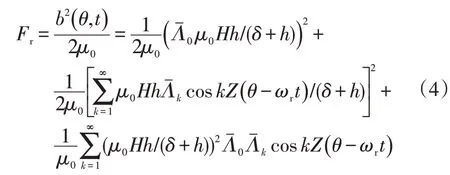
在式（4）中不难观察到，径向电磁力的表达式虽复杂，却只有3项，若气隙长度δ不随时间变化，则第1项为径向电磁力的静态分量，不随时间变化，因此不必考虑其对振动噪声的影响，第2项、第3项均具有时变特性，但由于大得多，通常只考虑第3项对振动噪声的影响[5]，若对第3项作傅里叶变换，则不难得出径向电磁力的主频率为转频与槽数的乘积及其整数倍：

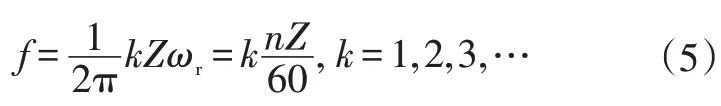
式中，n为电机转速。

3.3 不平衡电磁力来源及其理论分析

进一步研究发现，实际情况下电机转子齿上开有非对称辅助槽，左端3个，右端4个，如图4所示。

图4 转子齿上的辅助槽

电机开非对称辅助槽是因电机在实际生产过程中，由于转子冲片的质量不均匀、绕组在绕制过程中存在质量不对称、在绕组滴漆过程中绝缘漆分布不均匀等因素，造成转子质量的不均匀性，即引起转子质量不平衡问题[12]。因此，电机出厂前需进行动平衡矫正，一种常见的做法是在转子齿面开若干非对称辅助槽以对转子单侧减重，使转子质量沿径向均匀分布以满足动平衡要求。当开有辅助槽的转子齿进入其中一个极靴时，气隙长度δ将发生突变，记为δ′=δ+Δδ。同一时刻下，另一侧的气隙长度仍为δ，此时式（3）和式（4）中的δ将不再为常数，而是随时间和空间发生变化。换言之，此时气隙磁场分布不再对称，在开有辅助槽的转子齿面上，其磁通线的分布总是较相对侧的稀疏，这种不对称的气隙磁密必将引起不平衡的磁拉力[13]，可能引起异常的阶次噪声。

对于开有非对称辅助槽的电机，为了给转子单侧减重以满足动平衡要求，实际加工过程中随机性较大，无法定量描述转子齿面上每个辅助槽的深度、长度，且同一批次的电机辅助槽数量也不完全相同。但可以明确的是，此时在1个周期中气隙长度δ′不再为常数，式（4）中的3项均具有时变特性，径向电磁力的阶次特征将变得复杂，此时很难得到径向电磁力的解析解。因此，为了进一步研究，利用时步有限元法来定量分析磁钢所受电磁力以及定子壳体的结构振动响应的阶次特征。

4 基于时步有限元的电机仿真

时步有限元可用于求解瞬态电磁场问题，即对每一个时间步进行一次求解，得到该时刻的磁场分布，再通过后处理可得到电磁力的时域、频域特征。其本质是将模型离散成四面体单元，以在有限的空间域内求解经典的麦克斯韦（Maxwell）方程组：

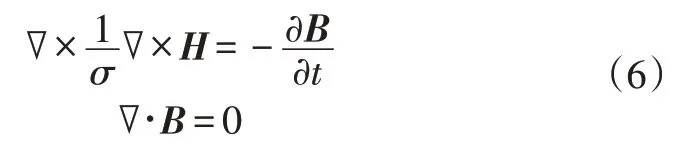
式中，∇为向量微分算子；H为磁场强度；B为磁通密度；σ为导体的电导率。

为保证足够的求解精度，模型关键位置（空间场变化迅速的区域）的网格应剖分得足够细致，且时间步也应取得足够小以满足对分析频率的要求。针对本文电机模型，由于其自身结构特性，常规的2D 仿真不再适用，须采用Maxwell 3D 建立电机有限元仿真全模型。为保证仿真精度，单独对磁钢、转子齿及气隙进行网格加密，最终电机整体模型网格数量共计约830 000 个，如图5所示。在瞬态电磁场中，基于时步有限元法的计算步长为0.25 ms，根据香农采样定理，分析频率上限为2 000 Hz，已包含上述异常阶次噪声问题所对应的频率。

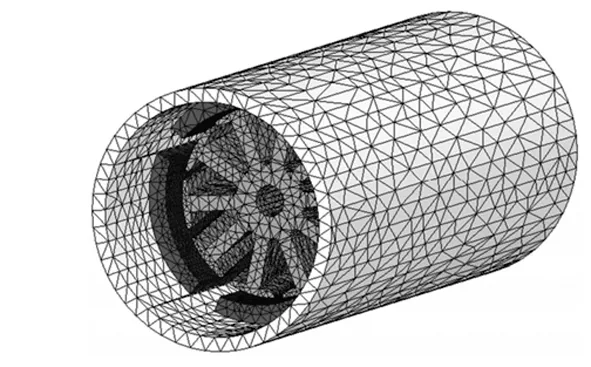
图5 电机有限元仿真模型

4.1 磁钢表面径向电磁力仿真分析

切向电磁力对圆筒形电机噪声的影响较小，因此仅考虑径向电磁力。若无特别说明，后文所提到的电磁力均为径向电磁力，所提到的阶次均表示频域上的阶次，而非空间阶次。为便于说明，将电机的4个磁钢按照逆时针顺序依次编号为1～4。Maxwell 3D将利用麦克斯韦应力张量法计算最后一个完整周期内各磁钢表面的电磁力密度。为分析磁钢所受电磁力的频域阶次特征，将每个磁钢表面上的电磁分布力沿磁钢内表面积分得到整个磁钢上的集中力，最后利用快速傅里叶变换得到每个磁钢电磁力幅值的频谱和4 个磁钢电磁力的相位谱。电磁力在单个磁钢上的分布云图如图6所示。

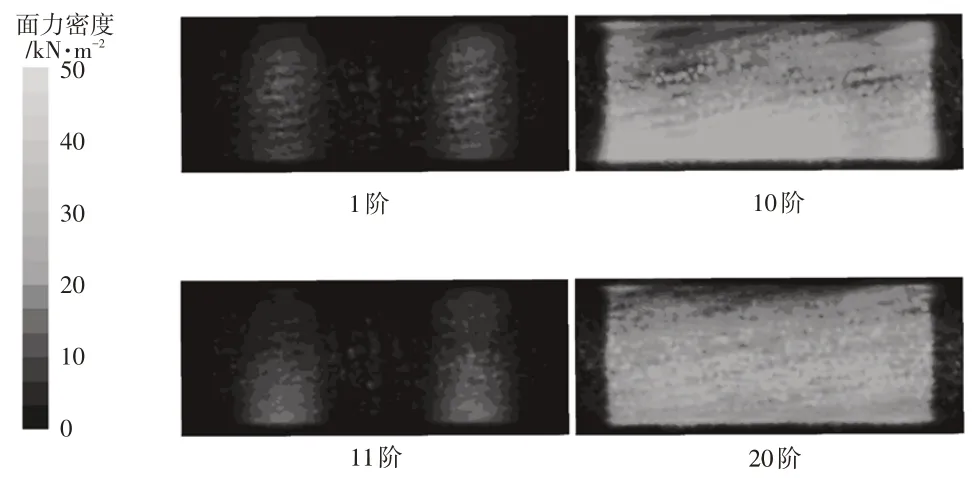
图6 不同阶次下单个磁钢表面的电磁力分布

单个磁钢径向电磁力频谱如图7所示，从单个磁钢受力情况来看，在2 000 Hz内，除电机原有的10阶和20阶主阶次外，转子齿面开槽引起了额外的电磁力阶次，如1阶、11阶等。不同阶次下各磁钢径向电磁力幅值如表2所示，相比原有的主阶次（10阶和20阶），各磁钢电磁力的11阶幅值明显偏小。

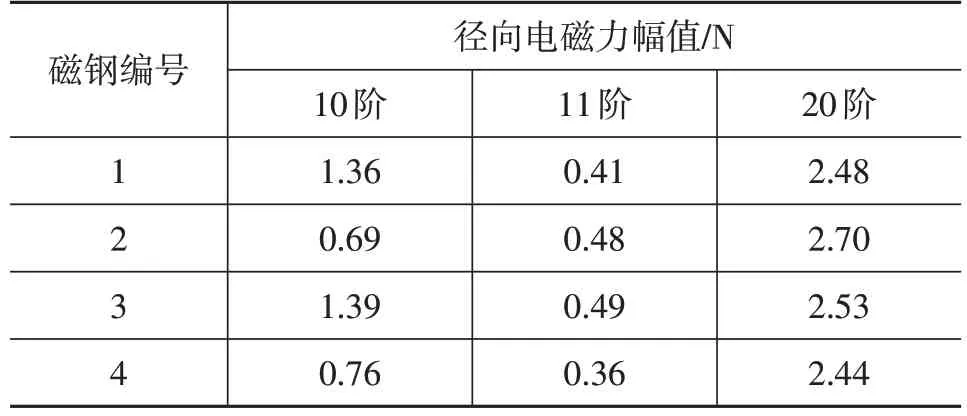
表2 不同阶次下各磁钢径向电磁力幅值

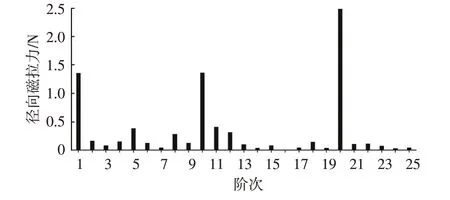
图7 单个磁钢径向电磁力频谱

不同阶次下各磁钢径向电磁力相位如表3所示，从4个磁钢受力的相位谱来看，针对第10、第20阶次，2组相对的磁钢（1号和3号，2号和4号）所受电磁力的相位近似相同，即相对磁钢受力方向几乎相反。因此，对整个电机而言，第10 阶次电磁力是近似平衡的，针对第11 阶次，2 组相对的磁钢（1 号和3 号，2 号和4 号）所受电磁力的相位相差约180°，即相对磁钢受力方向几乎相同。因此，对整个电机而言，第11阶次电磁力是严重不平衡的。

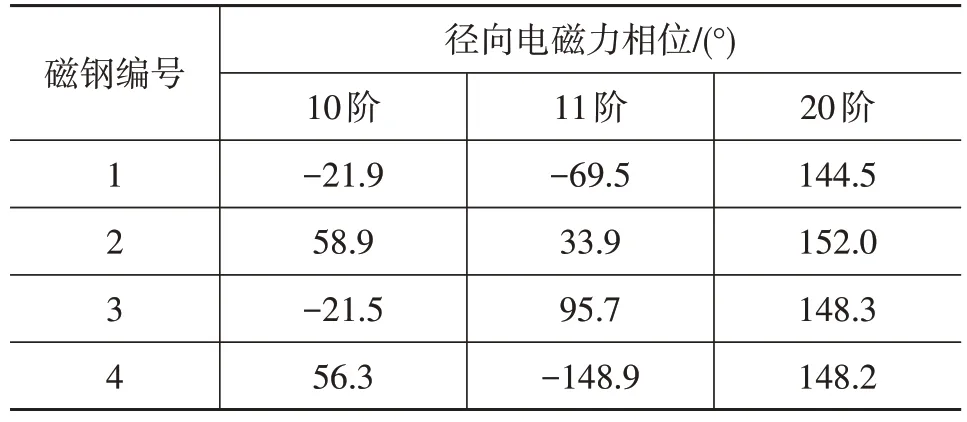
表3 不同阶次下各磁钢径向电磁力相位

为进一步形象说明不平衡电磁力的特性，根据表2、表3作出4个磁钢的精确受力矢量合成图，并比较10阶、20 阶与11 阶的不同，如图8 所示。在10 阶和20 阶次下，4 个磁钢的受力的合力很小，说明定子结构受力是近似平衡的；而对于11 阶而言，4 个磁钢受力的合力较大，说明定子结构受力严重不平衡。

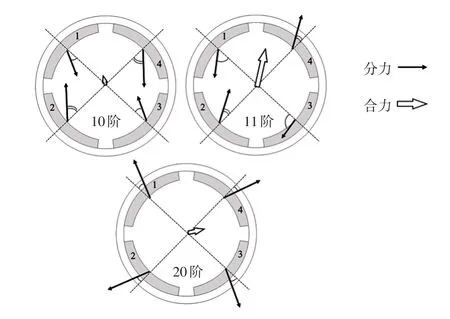
图8 不同阶次下4个磁钢受力矢量合成

以上有限元仿真结果是从相位分析的角度解释不平衡电磁力产生的原因。应当指出：电机振动阶次噪声不仅与某个阶次下单个磁钢的电磁力幅值有关，还与该阶次下各磁钢的电磁力相位有关。换言之，由于某个阶次的电磁力不平衡，该阶次的振动噪声极有可能在频谱图中占主导地位，即使该阶次下单个磁钢的电磁力幅值并不高。

4.2 定子壳体结构振动响应仿真分析

作用在磁钢表面上的电磁力本质上是应力[14]，在Maxwell中计算出最后一个周期的电磁力并作傅里叶变换，最后在频域中以节点力的形式映射到磁钢有限元结构模型上，以开展定子壳体结构的频率响应分析。在此过程中，要求电磁网格和结构网格大小尽量保持一致，以保证电磁力映射的准确性[15]。根据电机实际的安装情况，对定子壳体上的2 个螺栓孔施加固定约束，电磁力面密度映射及结构边界条件的施加如图9所示。

图9 定子壳体结构载荷施加及约束

为验证电磁力相位对结构振动响应的影响，将Maxwell 3D 计算所得的电磁力密度同时映射到4 个磁钢内表面，并与仅映射到1个磁钢内表面进行对照仿真分析。

有限元仿真结果如图10 所示。从图10 中可以看出：若仅考虑单个磁钢受力，此时结构的振动加速度响应可排除相位的影响，由于10阶电磁力幅值较11阶大，此时结构振动加速度响应的10 阶幅值也大于11 阶幅值，幅值最高的阶次为20阶；当同时考虑4个磁钢受力时，不仅要考虑各磁钢电磁力的幅值，还应考虑到相位差的关系，此时的仿真结果恰好相反，结构振动加速度响应的11阶幅值大于10阶幅值，且振动响应的11阶幅值尤为突出，这一特征与图3 所示的试验结果吻合，这从侧面说明了仿真结果的正确性。

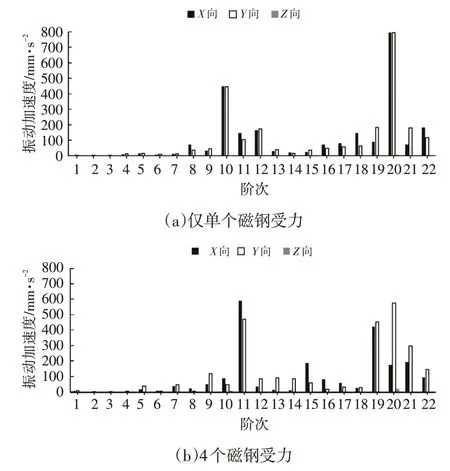
图10 定子壳体结构平均加速度响应

同时也注意到，当由单个磁钢受力状态切换到4个磁钢受力状态时，结构振动加速度响应的10 阶幅值也大幅下降，这是因为定子结构受力近似平衡导致。以上结果进一步说明，各磁钢所受电磁力的相位差对结构的振动响应有非常重要的影响，不平衡电磁力体现在各磁钢受力的相位差上。当4个磁钢受力不平衡时，定子壳体结构振动响应会放大，否则反之，正因如此，由非对称辅助槽引起的不平衡磁拉力导致了异常的11阶噪声的出现。

5 改进方案

如前所述，因改善转子动平衡问题而加工的非对称辅助槽使得电机气隙分布不对称，从而造成不平衡磁拉力作用在磁钢表面，最终引发了异常的阶次噪声。因此，解决这一问题的思路在于使气隙分布尽量对称，为此提出2 种改进方案：一是在保留非对称辅助槽的前提下，通过更加合理地分布辅助槽来削弱其产生的负面影响，即采用转子齿面等效减重法；二是舍弃非对称辅助槽，采用其他方式来改善动平衡问题，即采用转子配重法。前者的改进效果将利用CAE仿真手段进行验证，后者的改进效果将通过试制实物电机开展试验验证。

5.1 转子齿面等效减重法

注意到式（4）中Fr∝1/δ2，即径向电磁力反比于气隙长度的平方，这说明径向电磁力对气隙长度的突变极其敏感，依据此机理，提出转子齿面等效减重法，将因开非对称辅助槽而切削掉的部分转子质量均分到整个齿面上，每个齿面整面切削的厚度仅为0.08 mm，远小于原有的槽深，如图11所示。此时，在1个旋转周期中，气隙长度虽有突变，但不会过分剧烈，以在满足动平衡要求的同时尽量削弱不平衡磁拉力带来的影响。改进后仿真结果如图12所示，转子齿面经等效减重处理后，壳体振动响应的11 阶幅值大幅下降，转子齿面等效减重法取得了较好的效果。

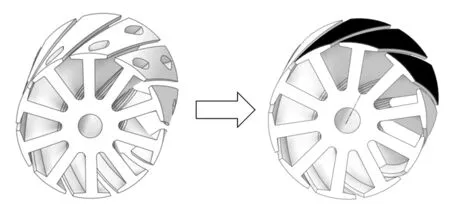
图11 转子齿面等效减重

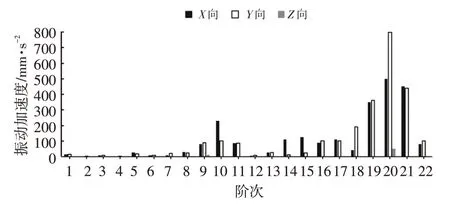
图12 定子壳体结构平均加速度响应（改进后）

5.2 转子配重法

采用转子配重方式来补偿动平衡的电机：在转子两端的绕组上增添环氧树脂，以改变转子质心，结合转子动平衡仪所监测的不平衡量，不断微调环氧树脂质量与位置，直至达到平衡状态。此时该电机转子齿面无任何辅助槽。对该电机进行升速工况噪声测试，该工况下输入电压由8 V逐渐提高至15 V，约束条件与仿真状态保持一致，测试环境如图13所示。

图13 转子加重的电机噪声测试

转子配重后的电机阶次噪声瀑布图如图14 所示，可以看出，在无非对称辅助槽的状态下，原有的异常阶次噪声，即11阶特征几乎消失，电机噪声主阶次为槽数10 的整数倍，这正说明异常的阶次噪声是由转子齿面的非对称辅助槽引起，采用转子配重法替代非对称辅助槽，可消除异常的11阶噪声特征。

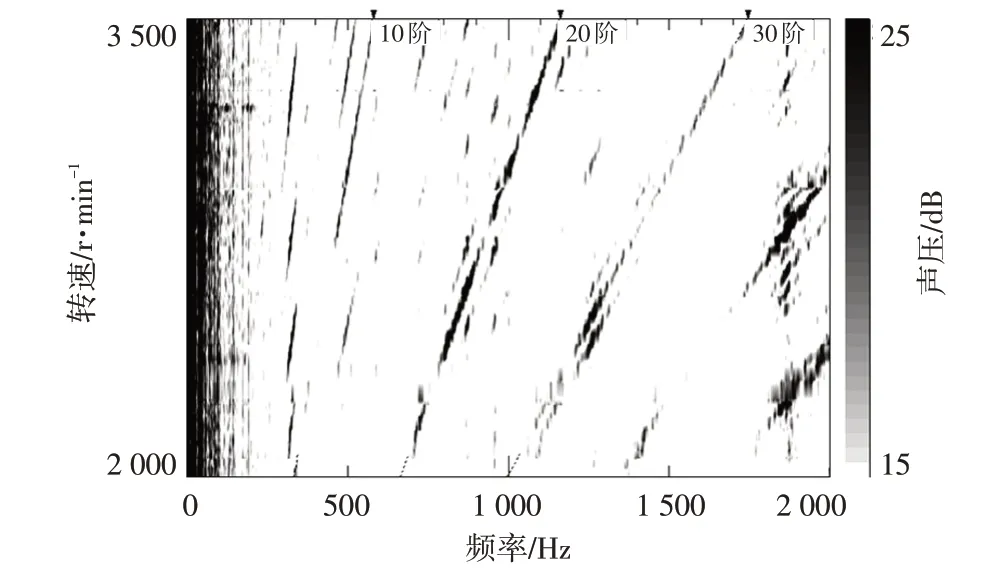
图14 转子加重的电机阶次噪声瀑布图

6 结束语

针对永磁直流电机出现异常阶次噪声的问题，本文从试验获取的噪声频谱特征出发，结合机理分析、仿真研究和试验验证，得出以下结论：

a.开非对称辅助槽的初衷是补偿转子动平衡，但这一矫正工艺会造成气隙磁密分布不对称，引起不平衡电磁力作用在定子结构上，最终在振动和噪声频谱中出现明显的异常阶次噪声。

b.在异常阶次下，单个磁钢所受电磁力的幅值并不高，但由于各磁钢受力相位差的影响，异常阶次下作用在整个电机壳体上的不平衡电磁力的合力超过了原有的主阶次，从而使得异常阶次在声振频谱图中占主导地位。

c.采用转子齿面等效减重法和转子配重法来保证动平衡，可有效解决因非对称辅助槽引起的电机异常阶次噪声问题。