泡沫金属微结构建模及其动态特性研究＊

罗耿 莫端钰 王童 陈轶嵩 孙世光

（1.长安大学，西安 710064；2.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082；3.西北工业大学，西安 710072）

主题词：泡沫金属 微结构 CT扫描 动态特性

1 前言

泡沫金属具有比强度高、比刚度高等优异的力学性能[1]，并且在压缩载荷作用下，既能承受很大的塑性变形，又能保持相对稳定的应力水平，具有良好的能量吸收特性[2]，近些年被用于设计各类防护和吸能结构，已在航空航天、建筑、车辆等领域广泛应用。

大多数泡沫金属采用发泡法制备，使其具有随机分布且复杂的细观结构，给泡沫金属数值研究工作带来了很大难度。早期，受技术手段限制，研究人员通常将胞孔结构简化为周期性排列的单胞模型[3-6]，不能准确地反映泡沫金属的真实细观结构，以致于不能准确地模拟泡沫金属的实际力学性能。目前，泡沫金属3D 细观随机分布有限元模型主要有2 种：Voronoi 有限元模型和基于CT 扫描图像建模的三维细观有限元模型[7-8]。Voronoi 模型建模过程与泡沫发泡制备过程类似，在很多文献中被用于表征泡沫金属的细观结构[9-14]。

随着计算机图像处理硬件技术的不断进步，基于CT扫描图像的泡沫金属有限元建模技术使准确模拟泡沫金属随机且复杂的细观结构成为可能。Michailidis等人[15-16]和Sun等人[17]分别建立了3D开孔和闭孔泡沫金属模型。但文献中所建立的基于CT扫描图像的有限元模型大多被用来研究泡沫金属在准静态加载条件下的力学特性，关于泡沫金属在动态载荷作用下的力学和变形特性的研究还较少。

泡沫金属在冲击载荷作用下表现出的动态特性主要为应力增强现象和局部变形现象[18]。目前，研究人员认为惯性效应是造成泡沫金属在动态冲击下应力增强的主要原因[19-20]，但对塑性冲击波与泡沫金属真实细观结构变形间的关系的研究还较少，基于CT 扫描图像的细观有限元模型无疑是研究该关系的有效路径。

综上所述，本文基于泡沫金属的CT 断层扫描影像信息重新构建泡沫金属三维数值模型，并通过准静态压缩试验对有限元模型进行验证；进而，基于CT扫描图像有限元模型开展泡沫金属动态加载仿真，研究塑性冲击波在泡沫金属中的传播机理，对泡沫金属在不同冲击速度下的变形模式进行讨论，并确定变形模式间的临界速度；最后对泡沫金属的动态吸能特性进行讨论。

2 泡沫金属微结构模型

2.1 CT扫描原理

采用微CT 断层扫描重构技术，可在不损坏试样的前提下快速重构泡沫金属的三维影像，其技术原理如图1所示。

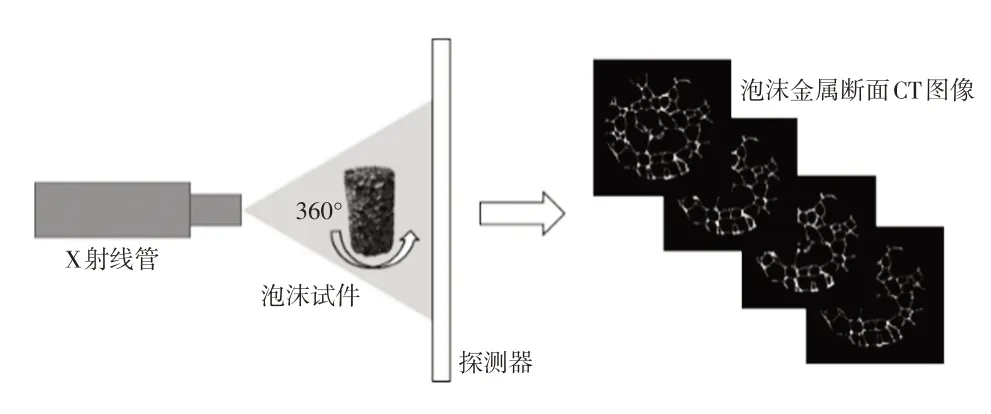
图1 CT扫描原理示意

2.2 二维影像处理与分析

利用CT 扫描设备对泡沫金属试件进行扫描，得到1 271张断面照片，层间距尺寸为0.014 5 mm，照片尺寸为2 000 像素×2 000 像素，1 个像素点对应实际尺寸0.014 5 mm。试件典型断面照片如图2a所示，其中灰色部分为泡沫金属试件的实体孔壁，黑色部分为中空胞孔，由图2a 可以清楚地看到泡沫金属试件各横截面胞孔的大小、形状及分布情况。试件孔壁非常薄，二维胞孔呈现为不规则的多边形，且胞孔大小不均。从二维截面图中未观察到泡沫金属试件内部存在大的缺陷。

通过CT扫描所得图像有的较暗，孔壁胞孔不明显，故需对断面图像进行处理。调节CT 扫描图像的对比度，将灰度图像转换为二值图像，处理前、后效果对比如图2所示。

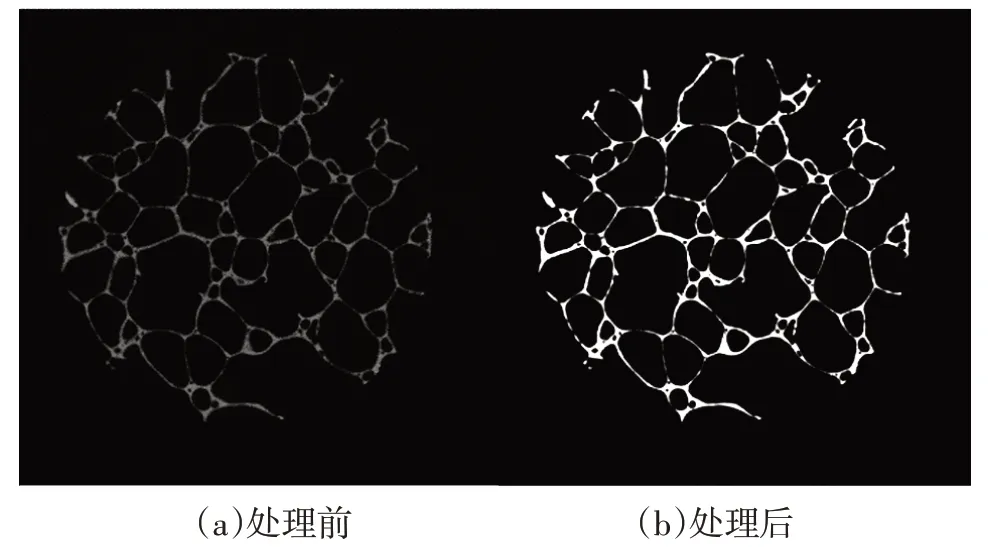
图2 试件截面处理前后对比

2.3 三维影像重构

泡沫金属三维影像重构在商用软件Mimics 中进行，将二值化CT 图像导入Mimics 中，生成泡沫金属三维点云模型，如图3所示。

图3 泡沫金属点云模型

由于泡沫金属胞壁结构十分复杂，无法通过直接实体化获得其几何模型，但是泡沫金属中的空隙部分相对规则，故可先构建空隙部分，然后通过布尔操作生成胞壁结构从而获得泡沫金属的细观模型，具体流程为：

a.在Mimics 中建立一个与试样同样大小的圆柱体，减去泡沫金属试样的3D点云模型，得到试样胞孔分布的三维点云模型，如图4所示。

图4 试样胞孔分布三维点云模型

b.将点云模型导入商用软件Geomagic Studio。同时，为方便开展数值仿真工作时施加边界并减少建模工作量，将圆柱体切成六面体，这样虽会造成胞元数量减少，但已有研究结果表明[21]，只需任一方向上胞元数量超过5个或6个，泡沫金属的宏观力学性能就不随细观胞元数量变化。

c.新建一个边长为15 mm 的立方体，经布尔运算，用立方体依次减去4 部分胞孔结构，即可得泡沫金属三维几何模型，过程如图5所示。

图5 泡沫金属几何模型建模过程

对胞孔数量、体积和表面积进行统计。首先将泡沫铝胞孔等效为规则球体，则泡沫金属胞孔的等效直径De为：

式中，V为胞孔的体积。

经统计得到泡沫金属的胞孔总数量为149个，孔径范围为1.45～6.46 mm，平均孔径为2.97 mm。厂商给出的泡沫金属平均孔径为2.88 mm，本文建模误差为3.12%，可见模型的孔径与实物吻合情况很好。孔径分布结果如图6所示：试件中孔径尺寸在2.0～2.5 mm区间内的胞孔数量最多，占胞孔总数量的22.8%；孔径尺寸在6.0～6.5 mm区间内的孔径数量最少，仅占胞孔总数量的1.3%。

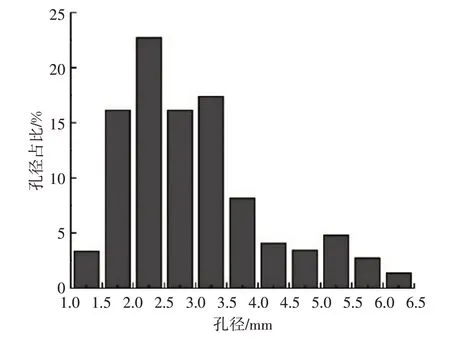
图6 泡沫金属孔径分布统计

实际泡沫金属的胞孔形状为光滑的不规则体，与球体相差甚远。为表征胞孔形状，定义与球体的相似程度为球度：

式中，S为与胞孔同体积的球体的表面积。

球度越接近1，说明胞孔的形状越接近球形。经统计，本文所建立的泡沫金属细观几何模型球度分布结果如图7 所示，球度分布范围为0.497～0.987，平均球度为0.789。由图7 可以看出，球度分布在＞0.7～0.8 区间的胞孔最多，占30.9%，其次是球度分布在＞0.9～1.0之间的胞孔，占26.8%，说明泡沫金属的胞孔形状并非很接近球形。

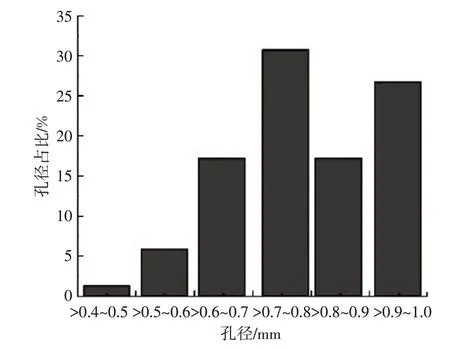
图7 泡沫金属球度分布统计

3 数值模型建立与验证

3.1 数值模型建立

采用ANSYS/ICEM 将泡沫金属的细观几何模型划分为四面体单元，共得到单元409 146个，划分结果如图8所示。

图8 泡沫金属模型网格划分结果

泡沫金属细观有限元模型如图9所示，上、下2块板均为刚性板，泡沫模型置于其间。对上板施加竖直向下的位移载荷，下板固定为支持端。泡沫和2个刚性板间设置接触，同时为泡沫金属本身设置自接触。泡沫金属孔壁材料为铝合金，其参数如表1所示[22]。

图9 泡沫金属细观有限元模型

表1 闭孔泡沫金属基体材料参数

3.2 数值模型的建立

为验证泡沫金属细观有限元模型的准确性，本文开展了泡沫金属准静态单轴压缩试验，采用万能试验机完成。准静态试验所用的泡沫金属试件尺寸为50 mm×50 mm×70 mm，与用于CT 扫描的泡沫金属从同一块泡沫金属材料上切割所得。试验采用位移控制，加载速度为1.5 mm/min。

泡沫金属准静态压缩试验与数值仿真名义应力-应变曲线对比如图10 所示。由图10 可知，2 条曲线吻合良好，表明本文所建立的细观有限元模型可对泡沫金属的宏观力学响应进行准确模拟。

蓝藻监测方面，由区环保局负责，以太湖流域第二大省际湖泊——淀山湖为重点，规定每年1—4月，逐月对淀山湖进行常规监测，5月起至10月止，对淀山湖实行人工加密监测。水质监测方面，青浦水环境监测分中心在淀山湖及其周边河道设置了14个监测点，以固定的频次采用国家标准方法进行7项水质指标监测，在中小河道水质监测上，设置73个常规水质监测点，每月1次进行水质监测。

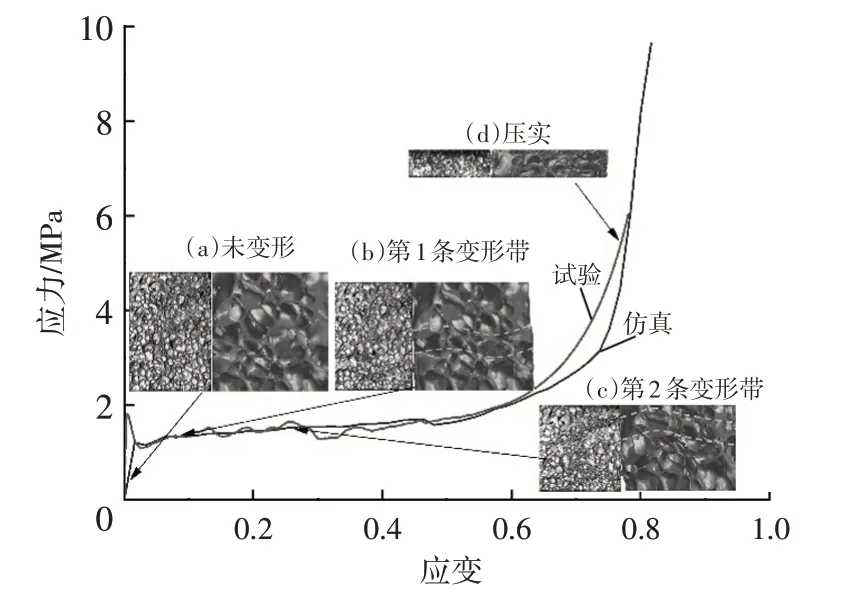
图10 数值仿真与准静态压缩试验应力-应变曲线及变形对比

图10 中也给出了在准静态压缩载荷作用下，试验和数值仿真中试件的变形过程，试验和数值仿真所呈现的变形形式相似。在泡沫金属静态压缩中，塑性屈服起始于泡沫金属的最薄弱部位，然后触发与其相邻的胞元坍塌，形成剪切变形带，如图10b所示。随着压缩继续，次薄弱区域出现塑性变形，形成第2条剪切带，如图10c所示。该过程不断重复，直至进入密实化阶段，如图10d 所示。在该阶段，泡沫金属被压实，胞壁相互挤压导致应力陡然上升。试验和数值仿真中变形模式的对比结果表明，有限元模型可准确模拟泡沫金属的细观变形特性。

4 泡沫金属动态特性

在冲击载荷作用下，泡沫金属的动态特性主要包括局部变形现象和应力增强现象。塑性冲击波是其动态特性形成的主要原因，本文将对泡沫金属在冲击载荷作用下的塑性冲击波效应开展详细研究，以对泡沫金属动态特性的机理进行解释。

4.1 塑性冲击波

基于细观有限元模型开展泡沫金属的动态加载仿真，当加载速度为150 m/s时，其变形过程以及泡沫金属冲击端和支撑端的名义应力-应变曲线如图11 所示。在冲击过程中，泡沫金属的塑性变形首先发生在冲击端，如图11c 所示，然后沿着冲击方向逐层向支撑端传播，如图11d、图11e 所示，该现象即泡沫金属的局部变形现象。沿着冲击方向逐层压溃的胞元在宏观上表现为一条塑性冲击波。在初始阶段，泡沫金属的冲击端首先产生弹性波，弹性波向着支撑端传过整个泡沫金属试样，使试样处于弹性变形状态。弹性波从冲击端传播到支撑端需要一定的时间，所以图中2 条应力-应变曲线存在时间差。

由图11可以发现，在塑性冲击波传播的过程中，冲击端和支撑端的应力基本保持稳定，且冲击端应力高于支撑端应力，该现象即泡沫金属的应力增强现象。由此可见，泡沫金属的局部变形现象和应力增强现象是同时出现且同时存在的。造成这一现象的原因是局部变形区域的应力水平高于未变形区域，塑性冲击波的波阵面为变形区域和未变形区域的分界面，因此造成了宏观层面上泡沫金属的应力增强现象。

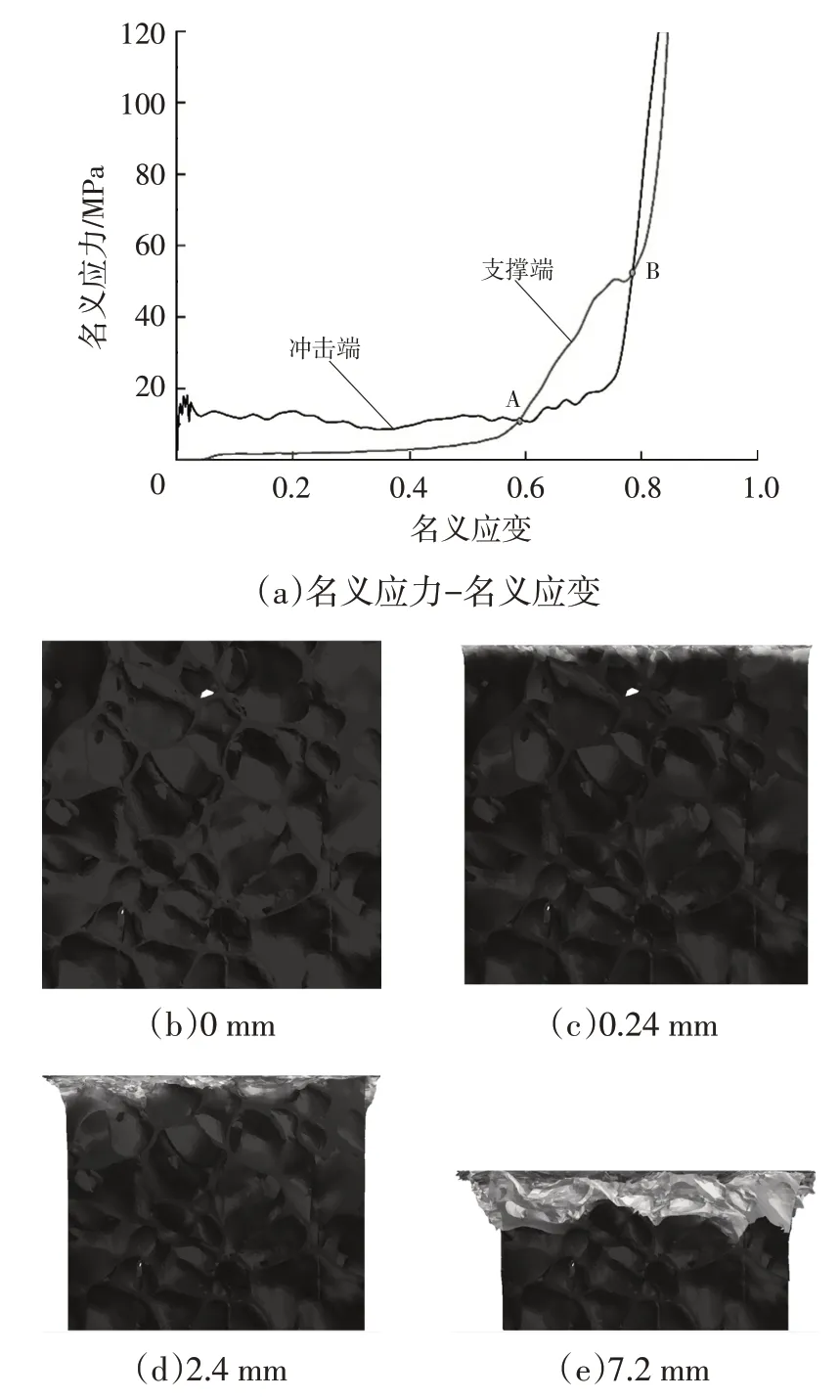
图11 冲击载荷下泡沫金属应力-应变曲线及变形过程

当波阵面抵达支撑端时，泡沫金属不存在未变形区域，可以认为冲击端应力等于支撑端应力，反映在其应力-应变曲线上即2条曲线的交点A。与此同时，波阵面在支撑端发生反射，因此支撑端应力迅速上升，直至塑性冲击波重新抵达冲击端。在此过程中泡沫金属已经相当密实，因此无法从细观有限元模型的变形中观察到塑性冲击波。为了更加直观地分析泡沫金属中塑性冲击波的传播规律，假设塑性冲击波由冲击端向支撑端传播时为第1次压缩阶段，塑性冲击波由支撑端向冲击端传播时为第2次压缩阶段，塑性冲击波的传播过程如图12所示。

图12 塑性冲击波在泡沫金属中的传播过程示意

图12 中：εL、εL2分别为第1 次压缩阶段和第2 次压缩阶段的锁定应变；σ0、σ1、σ2分别为泡沫金属准静态压缩下的平台应力、第1次压缩阶段冲击波阵面后区域应力和第2 次压缩阶段冲击波阵面后区域应力。由图12可知，泡沫金属两端的应力存在3 个平台阶段。在第1次压缩阶段（塑性冲击波向支撑端传播阶段）中，如图12b所示，支撑端应力小于冲击端应力。当塑性冲击波抵达支撑端时，支撑端应力发生阶跃，而冲击端应力保持不变，如图12c所示。在第2次压缩阶段（塑性冲击波向冲击端传播阶段）中，冲击端应力小于支撑端应力，如图12d所示，直至第2次压缩阶段结束。根据上述塑性冲击波在泡沫金属中的传播机理作出以下假设：由于弹性阶段十分短暂，忽略泡沫金属的弹性变形阶段；塑性冲击波在泡沫金属中传播的过程中，冲击端应力和支撑端应力保持不变；塑性冲击波的波阵面前、后区域的应力突变；塑性冲击波在端面反射时会引起波后区域应力出现阶跃。基于以上假设可以得到冲击载荷作用下泡沫金属的理想化材料模型，如图13所示。

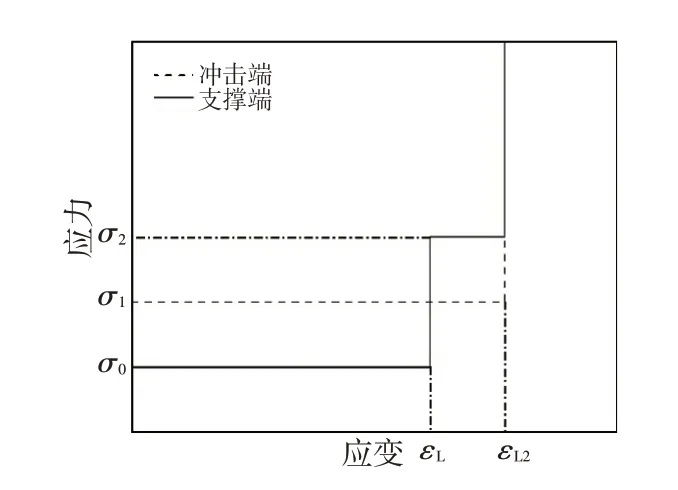
图13 泡沫金属理想化材料模型

对应图13 中的模型，应力和应变之间理想化关系表达式为：

式中，σi、σs分别为冲击端应力和支撑端应力。

可以发现，对于泡沫金属等多孔材料，由于在动态载荷作用下塑性冲击波（局部变形现象）存在，使得其内部应力分布不均匀（产生应力增强现象），因此，泡沫金属的动态理想化模型应该由2条曲线构成，用于描述其整体的应力状态。在已有的研究工作中，一般只关注了动态载荷作用下泡沫金属冲击端的应力变化情况，如图14 所示的刚性-理想塑性-锁定应变（Rigid-Perfect Plastic-Locking strain，RPPL）理想化材料模型，其中εd为压实应变，σqs为临界屈服应力。

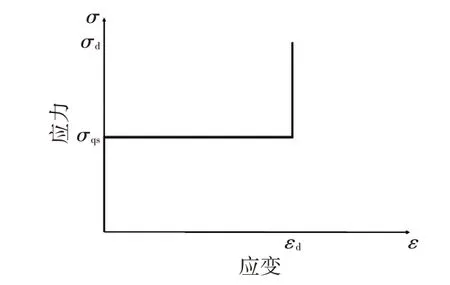
图14 泡沫金属RPPL理想化材料模型[23-24]

4.2 动态锁定应变

在前文建立的理想化材料模型中，最重要的参数为泡沫金属的锁定应变。基于有限元分析结果，当塑性冲击波形成并传播时，可认为波阵面后区域的变形程度达到锁定应变。因此，当塑性冲击波抵达支撑端时，泡沫金属的名义应变为该冲击速度下泡沫金属的锁定应变，可以通过测量此时泡沫金属的名义应变来获得泡沫金属的锁定应变。当冲击波传播到支撑端时，可以认为整个泡沫金属都在波阵面后方，材料中的质点都具有指向支撑端的速度，在这一刻，泡沫金属整体的动能最大。因此，可以根据泡沫金属在冲击过程中的动能最大值来确定泡沫金属的锁定应变。

本文计算了不同冲击速度下泡沫金属的动能随应变的变化关系，如图15所示。从图15中可以看到，随着速度的增大，泡沫金属动能最大值对应的应变增大，也就是泡沫金属的锁定应变增大。不同速度下动能最大值对应的应变即为泡沫金属不同冲击速度下的锁定应变。泡沫金属动态锁定应变随冲击速度的变化如图16所示，泡沫金属的锁定应变随着冲击速度的提高而增大，Tan等人[25]的工作也对相似的现象进行了描述。

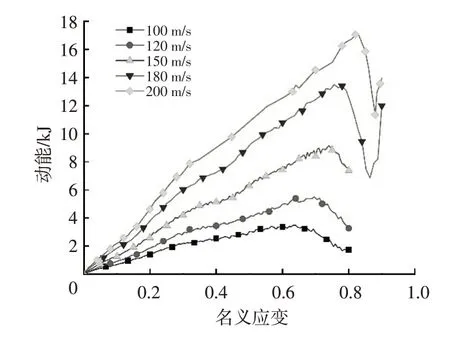
图15 不同速度下的动能应变曲线

图16 锁定应变随冲击速度变化曲线

4.3 变形模式

泡沫金属在冲击载荷下的变形模式与冲击速度密切相关。基于三维细观有限元模型，通过改变冲击速度，可以观察到泡沫金属不同的变形模式。图17 给出了泡沫金属在冲击速度为20 m/s、70 m/s和150 m/s时的变形模式。由图17可知，随着冲击速度的提高，泡沫金属的压缩呈现出不同的变形模式。根据变形特点，可将泡沫金属在冲击载荷下的压缩变形分为3种模式：在冲击速度较低时，其变形较为均匀，初始塑性变形发生在孔壁薄弱位置，称为均匀模式，如图17a所示；当冲击速度较高时，变形会高度集中在冲击端，形成一个很窄的变形带，并且从冲击端以逐层压溃的方式向支撑端传播，这种变形模式称为冲击模式，如图17c所示；当冲击速度介于上述2种变形模式对应的冲击速度之间时，泡沫金属没有形成明显的变形带，但变形靠近冲击端，同时泡沫金属试样薄弱孔壁处也会发生变形，这种变形模式称为过渡模式，如图17b所示。由图17可知，随着冲击速度的提高，泡沫金属内部逐渐形成明显的冲击波。相对应地，泡沫金属的变形模式也从过渡模式转变为冲击模式。

图17 泡沫金属在不同冲击速度下的变形模式

为研究泡沫金属的动态冲击行为，本文引入应力均匀化指标[26]：

可认为I=0.9时对应的速度为均匀模式向过渡模式转变的临界速度。

应用三维细观有限元模型计算了不同加载速度下的单轴压缩，得到应力-应变曲线，计算出了不同速度下的应力均匀化指标，如图18所示。从图18中可以看出，本文所用的泡沫金属模型从均匀模式向过渡模式转变的临界速度为50 m/s。

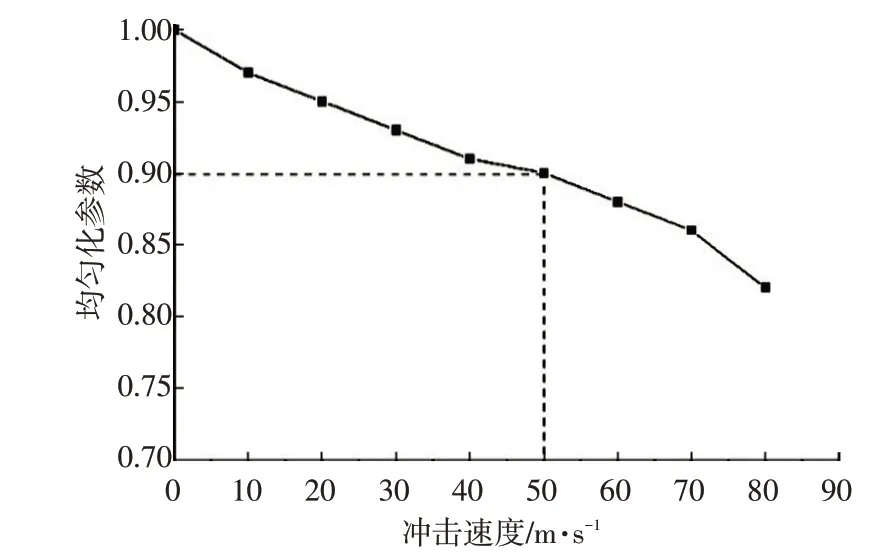
图18 不同加载速度下平台应力均匀化指标

4.4 动态吸能特性

泡沫金属在冲击载荷下的各项吸能特性指标与冲击速度的大小关系密切。在不同冲击速度下，泡沫金属冲击端名义应力-应变曲线如图19所示，随着冲击速度的提高，名义应力不断增大。通过泡沫金属的应力-应变曲线可以计算得到如下吸能指标：

图19 泡沫金属冲击端名义应力-应变曲线

a.总吸能EA，主要用于评价吸能结构在变形过程中通过塑性变形损耗的能量。

b.平台应力σp，表征吸能结构从开始屈服直到密实的整个过程中平均应力的大小，能比较直观地反映结构的吸能特性。

c.峰值应力Pm，表征冲击过程中结构刚开始发生屈服时受到的载荷。

图20所示为吸能、平台应力、峰值应力与冲击速度的关系，由图20 可知，泡沫金属在冲击载荷作用下，随着冲击速度的提高，总吸能EA、平台应力σp、峰值应力Pm均在不断提高。

图20 吸能、平台应力、峰值应力与冲击速度变化关系

5 结束语

本文基于微CT扫描技术获得了泡沫金属连续断面照片，并开展了泡沫金属微结构模型建模技术研究。同时，基于CT 扫描图像的细观有限元模型开展了一系列加载仿真，对泡沫金属动态特性进行了细致讨论，研究结果表明：

a.本文所建立的细观有限元模型，无论从细观上的胞元变形，或是宏观上的载荷-位移响应，均能准确模拟泡沫金属性能。

b.泡沫金属的胞元在细观层面上逐层压溃，造成宏观层面上的塑性冲击波传播和反射，导致出现局部变形现象和应力增强现象。同时，由于塑性冲击波反射，支撑端应力出现阶跃现象，传统理想化材料模型不能准确反映泡沫金属两端应力状态，本文建立的理想化材料模型能描述泡沫金属两端应力状态。

c.随着泡沫金属所受到的冲击速度提高，锁定应变也增大；同时，本文确定了泡沫金属的不同变形模式，分别为均匀模式、过渡模式、冲击模式，并引入均匀化指标，确定了均匀模式与过渡模式之间临界速度为50 m/s。

d.总吸能、平台应力和峰值载荷三者均随着冲击速度的提高而提高，泡沫金属的吸能特性随冲击速度的提高而有所增强。