节能赛车全路段滑行车速预测*

吴展骞 吴闯 赵治国

（同济大学，上海 201804）

主题词：节能车 降速模型 反向传播神经网络

1 前言

Z182原型车是面向壳牌环保马拉松与本田中国节能竞技大赛研发的比赛车型，其目标是在比赛规则允许的范围内，实现最低的燃油消耗量。速度分配策略对原型车燃油消耗量有较大的影响，Z182 原型车采取在17 km/h时点火加速，在37 km/h时怠速滑行交替的行驶策略。

国内外节能车队多从车辆的结构方面着手降低燃油消耗量，通过建立车辆降速模型预测加速点辅助驾驶的相关研究较少。王雪等[1]针对纯电动节能车提出一种行车策略及动力匹配方法，但其从电机、电池特性角度分析问题，对燃油车参考价值有限；姜长文等[2]通过采集车载全球定位系统（Global Positioning System，GPS）数据，基于反向传播（Back Propagation，BP）神经网络建立了节能车弯道降速模型，但该方法仅适用于弯道工况。在传统乘用车领域：Li 等[3]基于BP 神经网络和长短期记忆（Long Short-Term Memory，LSTM）算法建立了长程车速预测模型，但该方法实时性较差；Yan等[4]基于深度学习提出了一种车速预测方法，但该方法仅在城市道路低速工况下有较高的准确率，缺少对于内部道路的验证。因此，针对节能车全路段滑行降速特性的研究较为缺乏，研究节能车全路段滑行降速特性，预测加速点位置并提醒车手，对提高比赛成绩有重要意义。

本文以同济大学志远车队Z182 原型车为研究对象，建立车辆模型和Z182车型全路段BP神经网络降速预测模型，并应用于车手加速提醒系统，以达到减少燃油消耗量的目的。

2 节能赛车建模与CarSim仿真

2.1 节能赛车建模

车辆是一个多自由度的“质量-刚度-阻尼”系统[5]，对原型车建模时，应在保证模型准确性的同时忽略对目标影响较小的因素。本文针对Z182原型车的特点及所需求解的目标参数，进行了如下假设[6]：

a.Z182 原型车采用点火加速后断油滑行循环的策略，动力总成工作时间在车辆工作总时间中远占比小于1%，且本文主要分析赛车断油滑行时的动力特性，因此建模时将动力总成简化为一个刚体，并集中质量于底盘。

b.Z182原型车车轮与车架采用刚性连接，因此建模时忽略悬架的影响，不考虑轮胎弹性特性。

c.将Z182 原型车车壳、车架、动力总成、转向系统、车手均视为质量分布均匀的刚体。

Z182车型的基本外形尺寸和主要部件质量分别如表1、表2所示，各主要部件分布情况如图1所示。为便于计算，将车手简化为质量55 kg的圆柱体。

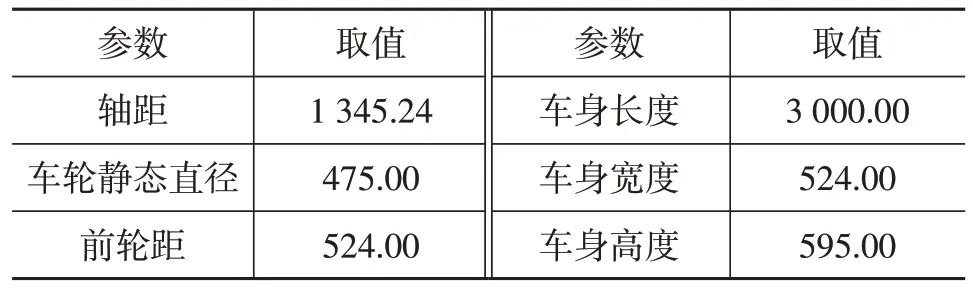
表1 Z182原型车基本外形尺寸 mm

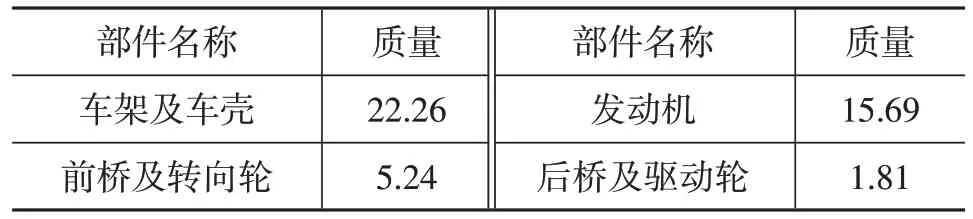
表2 Z182原型车主要部件质量 kg

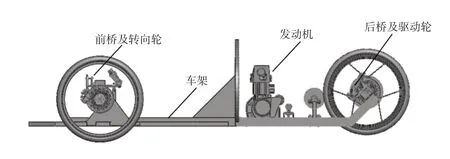
图1 Z182主要部件分布示意

Z182原型车的转动惯量如表3所示，空气动力学参数设置如表4所示，其中车辆坐标系原点位于车辆纵向对称面与前轴左右轮心连线的交点在地面的投影点处，X轴为车辆前进方向，向前为正，Z轴为铅锤（垂直）方向，向上为正，Y轴由右手螺旋原则确定。

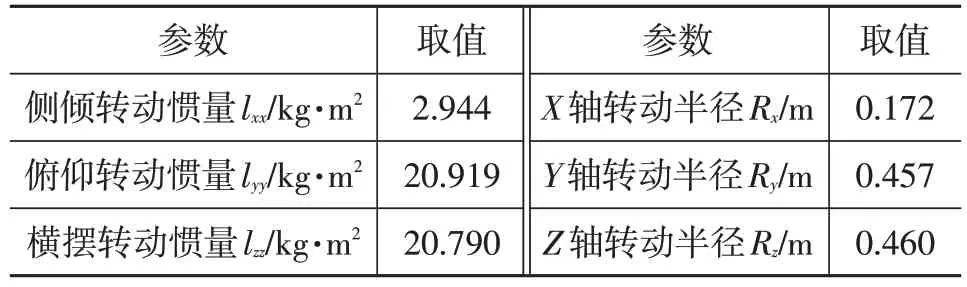
表3 Z182原型车转动惯量及相关参数

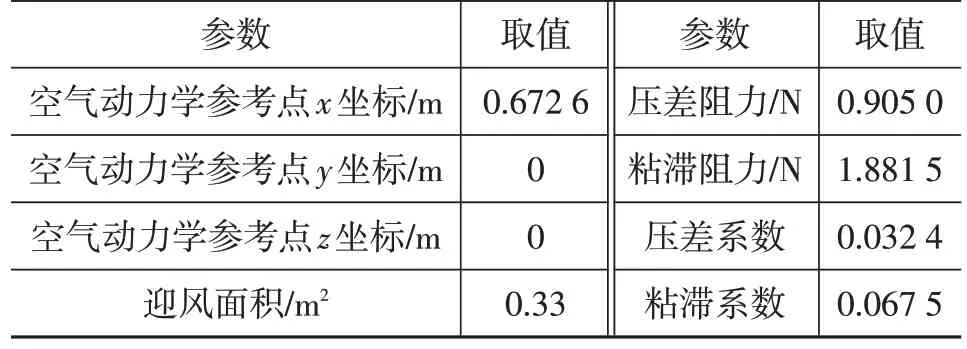
表4 Z182原型车空气动力学参数

Z182原型车轮胎特性设置如表5所示。

表5 Z182原型车轮胎特性参数

2.2 节能赛车降速特性仿真

仿真条件设置为：选择标准柏油路面，气温为25 ℃，路面附着系数为0.85，初始车速为37 km/h，空挡滑行，终点速度为17 km/h。选取直道和曲率半径30～70 m的弯道进行仿真。

通过CarSim 仿真采集数据点，绘得Z182 原型车不同工况下的降速曲线如图2所示。

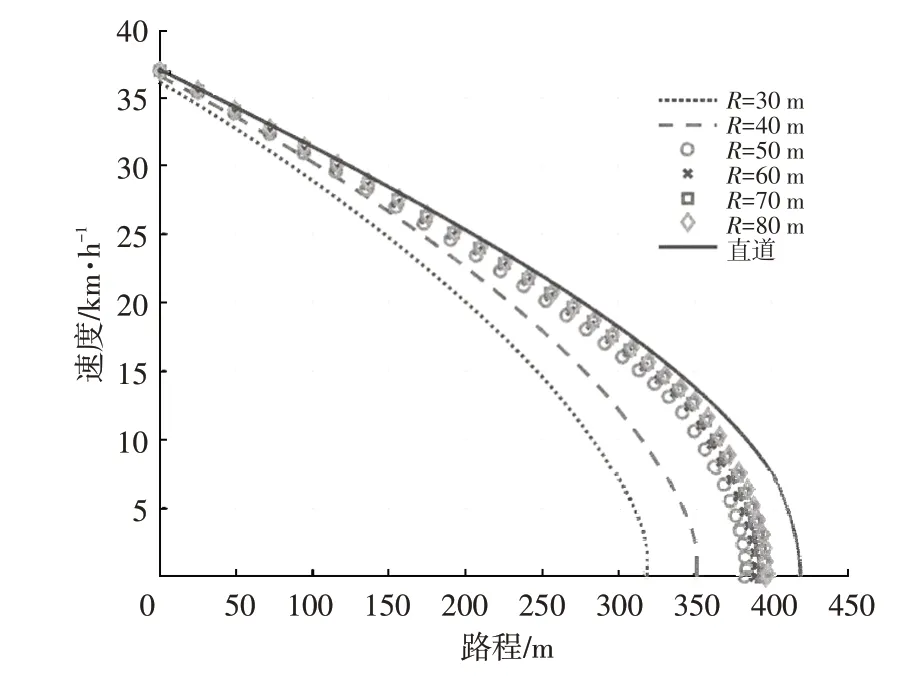
图2 Z182原型车多工况仿真降速特性曲线

由图2 可知，道路曲率半径越小，影响节能车速度下降的非线性因素影响越显著，因此本文选取实车试验数据中道路曲率半径最小的一组数据与仿真结果进行对比。道路曲率半径R=50 m时模型仿真结果与实车在相同条件下获取的试验数据对比结果如图3所示，由图3 可知：该模型在5～37 km/h 的速度区间内同一坐标位置下与实车试验数据误差小于0.6 km/h，能较好地表现Z182车型速度下降的特性；在小于5 km的非线性段，由于非线性影响因素部分作用显著，模型速度下降特性与实车速度下降特性误差逐渐增大。本文所涉及的速度区间为17～37 km/h，在该速度区间下，该模型具有较高的准确性。

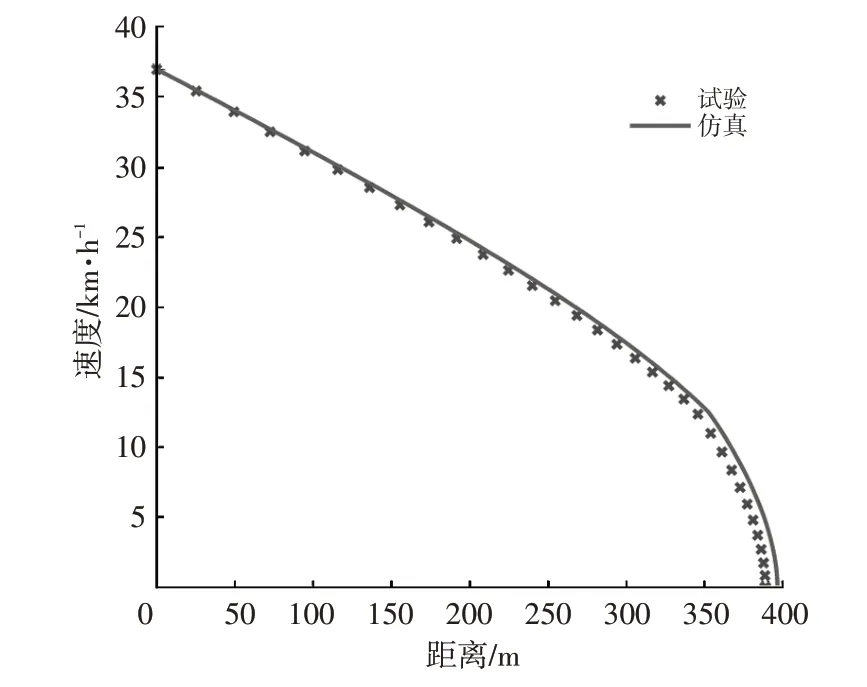
图3 模型准确性验证

3 基于BP神经网络的节能车全路段降速模型

3.1 BP神经网络搭建

由模型仿真结果可知，节能车降速过程是非线性的，受到车型、弯道曲率半径、速度等多种因素影响，传统的线性预测方法存在一定的局限性。BP神经网络可以不断利用误差进行反向传播，是良好的学习特征和自组织学习方法，对于特征复杂和不清晰的数据进行分类和识别具有良好效果[7]，由于其良好的非线性逼近能力而得到了广泛的应用[8]。因此，本文选用BP神经网络预测节能车降速过程。

n输入的人工神经元模型如图4 所示，主要包括连接权值、求和单元及激活函数3 个部分[9]。其中x1～xn为神经元i的n个输入变量，为对系统模型有关键影响的自变量，ωi1～ωin为神经元i的n个连接权值，ui为神经元i的激活函数φ()的输入，定义为：

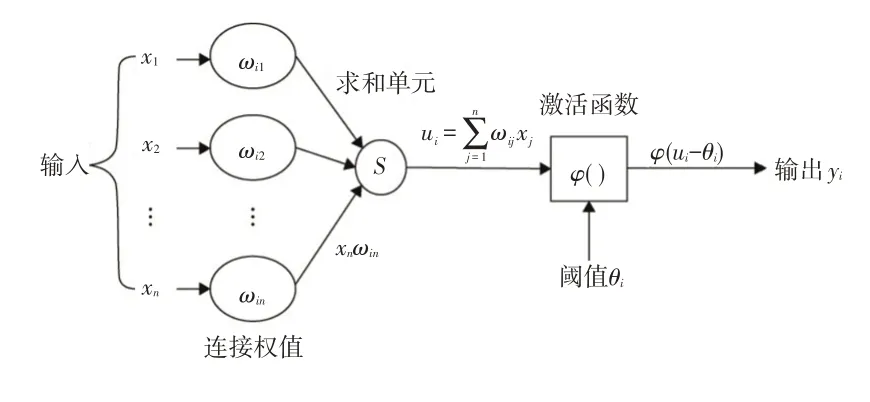
图4 人工神经元模型

Sigmoid 由于在正半轴的函数性质与常规的神经元模型LIF 模型十分相似，曾一度作为深度学习的激活函数而广泛使用[10]。故本文所选激活函数φ()采用Sigmoid函数：

神经元i的输出yi定义为：

式中，θi为神经元i的阈值。

将单一神经元通过图5 所示的方式连接构成本文所使用的BP神经网络，其中输入层神经元数量为4个，隐含层神经元数量为10个，输出层神经元数量为1个。

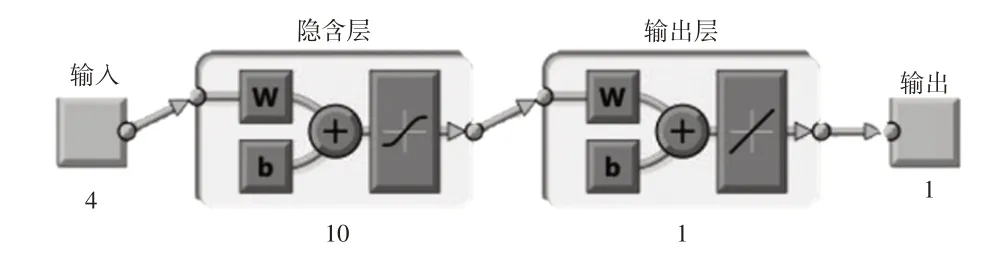
图5 BP神经网络结构

节能车在无坡度无风环境下直道滑行时的阻力F为：

节能车在无坡度无风环境下直道滑行时的加速度a为：

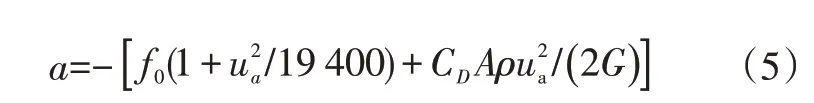
而在转弯行驶时，车辆的滚动阻力接近直线行驶的150%～200%[11]。

因此，影响节能车降速特性的主要因素有车辆自身特性、车辆行驶速度及道路曲率半径。为了预测节能车在特定路段的速度下降特性，选取车型序号、初始速度v、道路曲率半径p与预测段道路长度s的CarSim仿真数据作为输入，其中车型序号用以表征车辆自身特性，仿真输出为节能车在预测路段末端的速度。

为解决输入数据集变量单位数量级不统一的问题，引入归一化函数将数据样本映射到0～1的区间内：

式中，y(x)为离差化标准值；xmin、xmax分别为该变量最小值和最大值。

隐含层节点数量q为[10]：

式中，L为输入层神经元数量；M为输出层神经元数量；C为1～10范围内的常数。

由式（7）可知，q的取值范围为5～14。通过选取不同的隐含层节点数量q训练模型，通过验证得出q=10个时模型具有最小误差，故该模型最佳隐含层神经元数量为11个。

本文利用MATLAB BP 神经网络工具箱搭建BP 神经网络模型，采用Levenberg-Marquardt法对模型进行训练。训练集、测试集、验证集比例为70%、15%、15%，其中训练集、测试集为2.2节中的数据集，验证集为实车数据。

3.2 BP神经网络训练

该BP 神经网络的训练过程曲线如图6 所示，该BP神经网络最小均方差出现在第136次，其最优均方差为0.005 829 7，符合预期指标，故依据该组迭代结果，获得最终的BP神经网络。

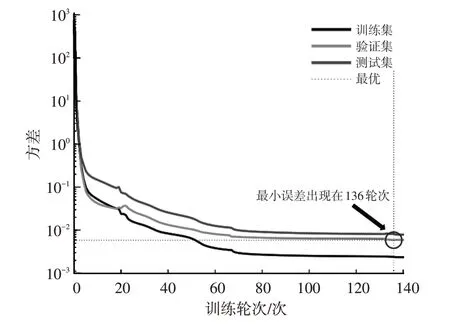
图6 BP学习过程曲线

本文使用决定系数R2作为预测结果准确度的衡量标准：

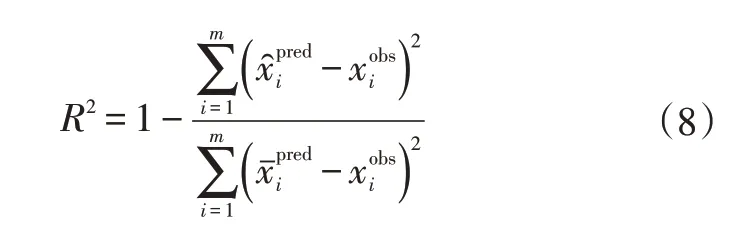
式中，m为测试集样本数量；xipred为末端速度预测值；xiobs为实际末端速度。

图7 所示分别为训练集、验证集、测试集和全部数据集拟合值与试验值的线性回归比较结果，通过验证，该网络R2＞0.999，拟合效果良好，能够充分反映Z182原型车在不同条件下的降速特性。

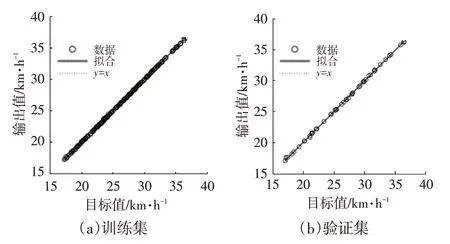
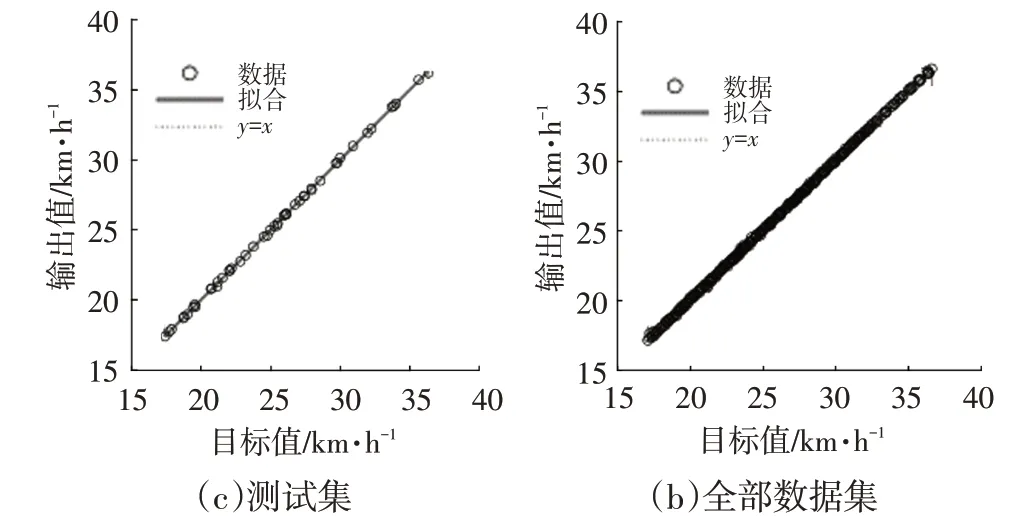
图7 拟合值与真实值线性回归比较

3.3 BP神经网络验证

为进一步检验该网络的实用性，本文使用Z182 原型车在北京京港国际赛车场和同济大学试车场分别进行4组降速测试。试验车辆行驶路径如图8所示，所选取的行驶工况能够覆盖节能车行驶的全部工况。

图8 神经网络验证试验路径

图9 示分别为赛车通过某一特定区间路段的尾速的实车数据和在该区间终点前25 m 处使用BP 神经网络预测的赛车通过该特定区间路段的尾速。从图9 中可以得出，该BP 网络对车辆在特定区间路段下的尾速预测结果误差均小于0.3 km/h，能够较为准确地反映节能赛车速度下降特性。

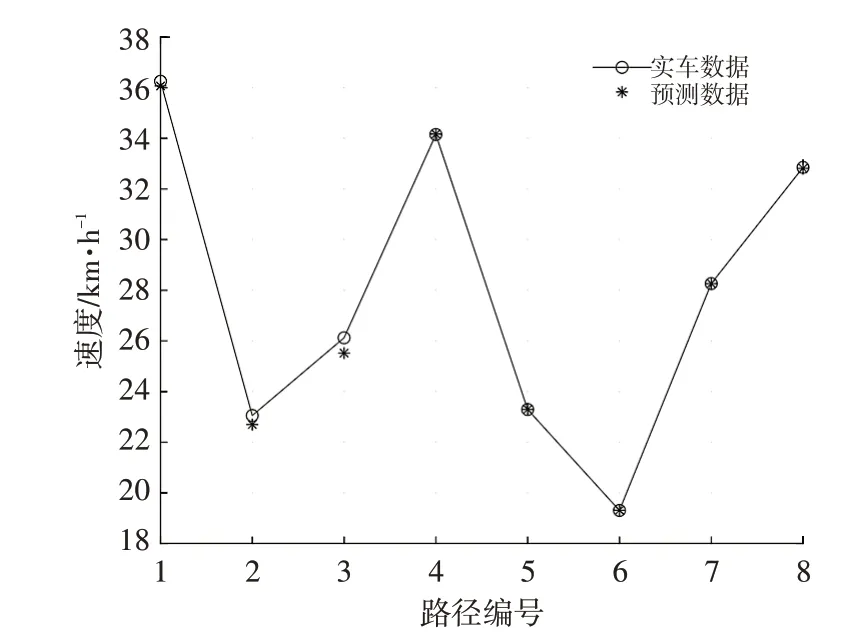
图9 BP神经网络验证

4 试验与结果分析

基于上述研究，为了进一步验证全路段BP 神经网络降速预测模型的有效性，在Z182 车型上进行试验。与传统节能车相比，该车加装了霍尔轮速传感器、GPS传感器和用于与电脑上位机通讯的433 MHz 无线发射模块。试验车辆如图10所示。

图10 试验车辆

在试验过程中，首先建立道路GPS 坐标地图，由霍尔轮速传感器、GPS 传感器采集车辆位置和速度信息，通过433 MHz 无线发射模块与MATLAB 进行通讯，BP神经网络根据回传的信息解算出加速点与当前位置的距离，将该预测结果与车速实际降低到最优加速值（17 km/h）的位置进行对比，验证其准确性。

实车试验地点为同济大学试车场，车辆行驶路径包含图8b 中的路径，覆盖节能车行驶的全部工况。上位机反馈结果如图11所示。

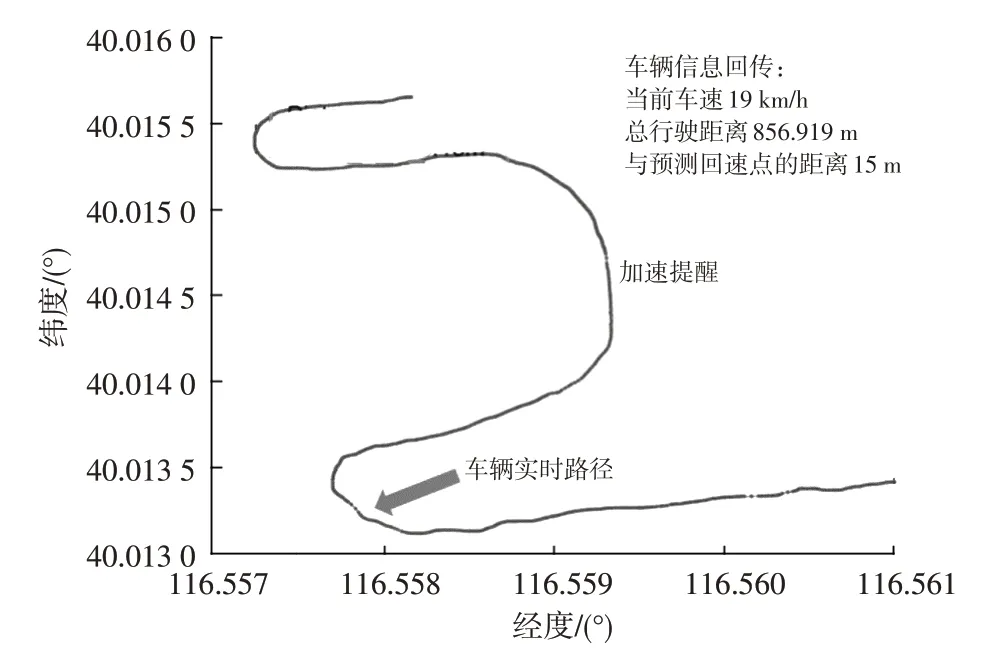
图11 MATLAB上位机反馈界面

在试验中，当车速降至25 km/h时，开始采集车辆参数并发送至上位机解算。试验结果如表6所示，准确度用误差率（预测误差距离与单次滑行总距离的比值）表征。在本文试验条件下，该模型能够平均提前5.15 s预测加速点位置，单次平均误差率小于0.1%，具有较好的实用价值。

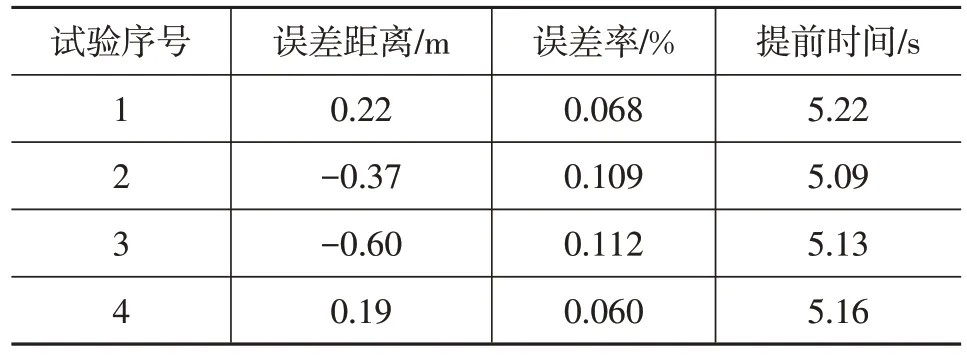
表6 BP神经网络预测试验结果

通过将该模型引入车载系统，在车速降至25 km/h时，开始采集车辆参数并发送至上位机解算，并通过声音频率的高低表征车辆与理论最优加速点的距离，提醒车手及时采取操作。该系统的作用以误操作次数表征，误操作指车手加速位置与理论最优加速点偏差大于±5 m。如表7所示，使用该系统后，平均减少4.07%的燃油消耗量。

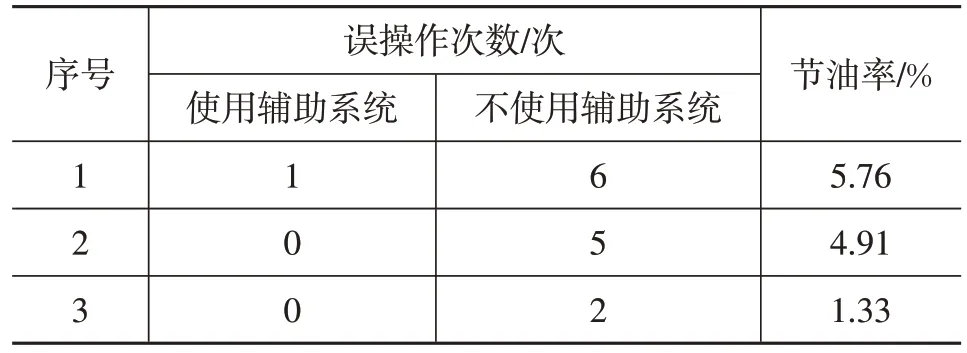
表7 辅助系统使用前后成绩对比

5 结束语

本文基于BP 神经网络构建了Z182 节能车全路段降速模型，可实现对节能车加速位置的预测。自主搭建了试验平台，通过实车试验，该模型平均能够提前5.15 s预测加速点位置，单次平均误差率小于0.1%，通过引入该模型，结合相应的车载辅助设备，单次试车平均能减少4.07%的燃油消耗量。

试验结果表明，该模型能够准确预测节能车加速位置，同时，本文为研究节能车比赛速度分配提供了一种新的思路，但是本文仅将其用于辅助车手操作，后续可将其应用于车辆控制系统，实现车辆最优速度分配的自动控制。