假设检验在汽车排放实验室比对中的应用研究

石则强 师颖 曹宁 朱晓轩 拓万航

（中公高远（北京）汽车检测技术有限公司，北京 101103）

主题词：假设检验 排放试验 实验室比对 置信区间 置信概率 正态分布

1 前言

2020 年11 月30 日，中国合格评定国家认可委员会（China National Accreditation Service for Conformity Assessment，CNAS）发布了CNAS-CL01-A005:2020《检测和校准实验室能力认可准则在汽车和摩托车检测领域的应用说明》[1]，要求汽车排放实验室“应至少每2年参加1 次能力验证或与获CNAS 认可的另外两家（含）以上实验室进行比对，且实验室比对/能力验证的结果不超出实验室比对/能力验证方案预定的评价准则”。该文件对实验室比对的方案和评价准则未作规定。GB/T 28043—2019《利用实验室间比对进行能力验证的统计方法》[2]推荐了多种能力评定指定值、标准差和统计量的计算方法，但多采用经验值进行评价，不能帮助实验室定位技术水平，不能通过实验室比对达到保证试验结果准确性、提升实验室技术水平的目的。

本文采用数理统计中的假设检验方法，通过分析比对数据的正态性、2 个正态总体的方差齐性和均值差，结合置信区间和标准差，实现实验室比对的评价。

2 实验室比对原始数据及评价方法差异

2020 年，轻型汽车排放检测行业组织完成了排放Ⅰ型实验室比对，共有11家实验室参加比对，其中的一氧化碳（CO）比对数据如表1所示。由表1可以看出，按照常用的Z比分数评价方法，所有实验室均为满意结果，但实验室间的测量结果存在较大波动，实验室8 和实验室9 的实验室间百分差达到了-29.1%和22.2%，实验室内的数据分散程度也存在较大差别，实验室10 和实验室11 的实验室内相对标准差分别为17.1%和10.8%。显然，Z比分数、百分差和标准差的评价结果存在很大差异。

表1 排放Ⅰ型实验室比对CO数据

3 假设检验用于实验室比对的分析方法

3.1 假设检验的原理

利用概率性质的反证法进行假设检验[3]：设某个假设H0需检验，先假定H0为正确，在此“假定”下，合理地构造一个事件A，在H0为正确的条件下，A 为一个小概率事件。

假设检验的一般步骤为：

a.根据问题提出原假设H0与备择假设H1；

b.构造检验统计量，根据原假设H0与备择假设H1确定拒绝域的形式；

c.选定适当的显著性水平α，求出临界值，得到对原假设H0的拒绝域；

d.计算检验统计量，与临界值比较，若满足拒绝域，则拒绝H0，否则接受H0。

使用假设检验进行实验室比对分析的步骤如下：

a.进行样本正态性检验；

b.利用F检验判断方差齐性；

c.利用t检验判断均值差；

d.计算样本总体的置信区间；

e.制作t检验统计图，进行比对分析。

3.2 样本正态性检验（W检验法）

假设检验分析方法分为正态总体和非正态总体2种类型。为了确认样本分布的类型，采用W检验法进行正态性验证[3]，W检验统计量为：

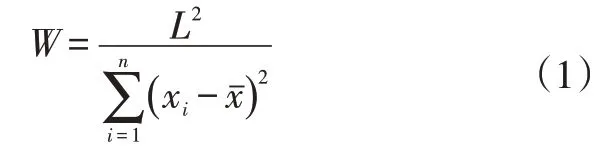
式中，n为样本中数据数量；xi为样本第i个数据为样本平均值查《夏皮罗-威尔克检验计算统计量W所必须的系数表》[3]得出。

对所有的实验室样本构造W检验统计量计算表，得出W=0.973，并查《夏皮罗-威尔克检验计算统计量W的概率分位数表》[3]得出W检验分位数Wa=0.931，满足Wa＜W≤1，即样本总体服从正态分布，同样也可验证各实验室的样本均服从正态分布。

3.3 2个正态总体方差的假设检验（F检验）

将单个实验室和实验室总体样本分别记作ξ～N(μ1,σ12)和ξ～N(μ2,σ22)，检验2个总体的方差齐性，即F检验[3]。

假设：

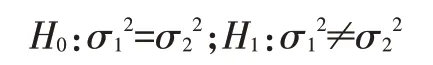
根据F检验法，F检验统计量为：

F检验临界值Fc=F1-α/2(n1-1,n2-1)，根据2 个样本的数据数量n1、n2和显著性水平α，可查《F分布分位数表》[3]得到。

当Fs＜Fc时，接受H0，认为2 组试验样本方差相等；否则，拒绝H0。

表2 所示为F检验统计量计算结果。由表2 可知，各实验室的Fs均小于Fc，即接受H0，单个实验室样本与实验室总体的方差相等，认为各实验室样本与实验室总体样本之间的数据无显著偏离。

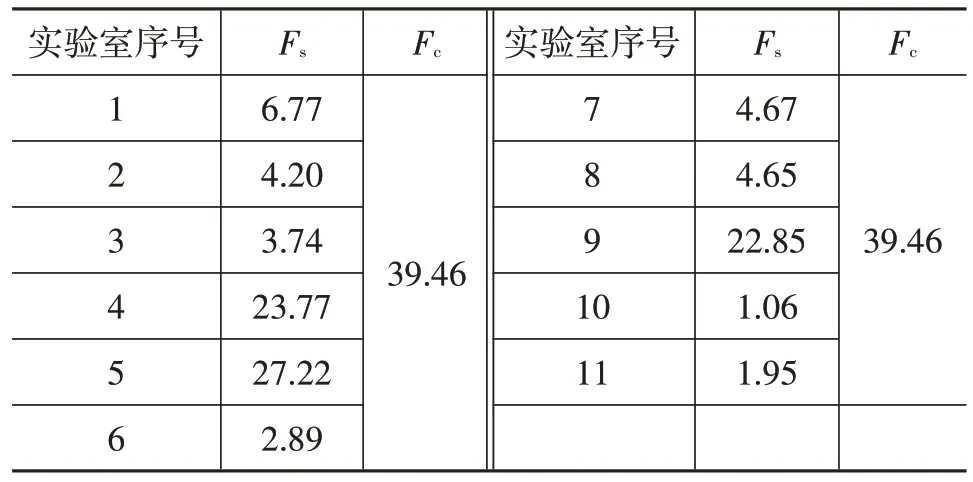
表2 F检验统计量

3.4 2个正态总体均值差的假设检验（t检验）

各实验室样本与实验室总体样本均服从正态分布，且σ12=σ22，检验两正态总体均值差，即t检验[3]。

假设：

根据t检验法，t检验统计量为：

t检验临界值tc=t1-α/2(n1+n2-2)，根据样本数量n1、n2和显著性水平α，可查《t分布分位数表》[3]得到。

当-tc＜ts＜tc时，接受H0，认为2 组试验样本差异不显著；否则，拒绝H0。

表3所示为t检验统计量计算结果。由表3可知：实验室2 和实验室9 的ts＞tc，实验室8 的ts＜-tc，均拒绝H0，与实验室总体样本的差异明显；其余实验室的ts均接受H0，与实验室总体样本间的差异不明显。

表3 t检验统计量

3.5 2个正态总体均值差的置信区间

由F检验可知，各实验室与实验室总体样本的方差相等，即，在显著性水平a=0.05 下，实验室总体样本估计均值差的置信区间为[3]：

本文按照宽松的要求，将|ts|最大的实验室8样本作为ξ～N(μ1,σ12)，计算得出实验室总体样本的置信区间为[49.50,71.75]mg/km。

3.6 假设检验样本分析

各实验室CO、THC和NOx测量结果与t检验统计结果分别如图1～图3所示。

图1 CO测量结果与t检验统计结果

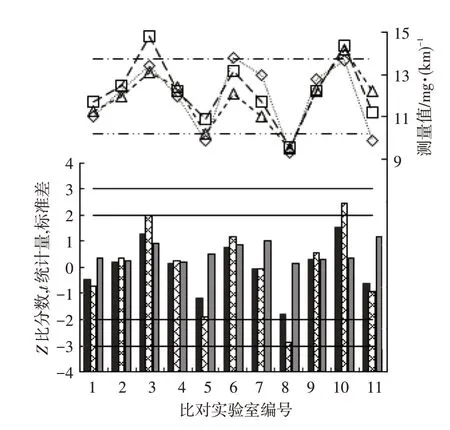
图2 THC测量结果与t检验统计结果

图3 NOx测量结果与t检验统计结果

由图1可以看出，t检验统计量与Z比分数相比：a.两者的样本评价结果趋势基本一致；

b.使用Z比分数评价，所有实验室的样本均满意，使用t检验评价，3 个实验室的样本超出临界值，其样本分布状态明显偏离；

c.ts最大的实验室9，样本全部超出置信区间上限，标准差最小，表明实验室水平较好，但试验存在系统性误差；

d.ts最小的实验室8，样本全部超出置信区间下限，标准差适中，表明实验室技术水平与其他实验室相当，但试验存在系统性误差；

e.实验室2 的标准差适中，但个别样本超出置信区间上限，导致ts＞tc，表明实验室技术水平与其他实验室相当，但试验存在系统性误差；

f.实验室10的标准差最大，个别样本低于置信区间下限，但其Z比分数和ts均未出现异常，表明实验室运转正常，但技术水平稍差；

g.实验室11 的标准差偏大，样本均在置信区间内，Z比分数和ts均无异常，表明实验室运转正常，但技术水平不稳定。

从图2和图3可以看出，t检验同样适用于各实验室THC和NOx样本的分析。

由此可以认为，使用假设检验方法分析汽车排放实验室比对的样本，与Z比分数方法的结论趋势相同，结合置信区间与标准偏差，可帮助实验室定位技术水平状态。

4 结论

a.使用假设检验进行排放实验室比对分析，与Z比分数的结论趋势相同；

b.ts超出tc，可做不满意评价；

c.假设检验采用了置信概率和置信区间的概念，所得结论能够反映比对结果的真实情况；

d.假设检验方法与标准差相结合，可定位实验室的技术水平状态。