稀疏规则库模糊插值推理的模糊结构元算法
薛胜寒,郭嗣琮
(1. 辽宁工程技术大学 理学院,辽宁 阜新 123000;2. 辽宁工程技术大学 智能工程与数学研究院,辽宁 阜新 123000)
0 引言
模糊推理的合成推理方法(Compositional Rule of Inference,CRI)是由ZADEH L A于1973年的提出[1],它不仅是模糊系统控制重要的理论基础,还广泛应用在故障检测、医疗诊断、自动驾驶、金融分析、风险预测等领域,发挥着越来越重要作用.
在稀疏规则库条件下,推理规则前件因素的状态域不能被规则库的前件状态所覆盖的时候,即规则前件的隶属函数之间就会出现空隙,因而,由于缺少相应的推理依据使得传统的模糊推理方法遇到困难.在此基础上,KOCZY L和HIROTA K[2]最早提出了KH线性插值推理方法,解决了模糊规则库呈稀疏状态下的模糊推理问题.但众多学者发现KH线性插值推理方法并不能保证最后推理结果的隶属函数是一个正规凸集,于是,提出了很多改进的插值推理方法.王天江[3]等提出了相似插值推理方法,该方法基于隶属函数围成的图形,更具有直观性.WANG Baowen[4]等提出了Lagrange插值推理方法,基于各种类型的函数有着不同的计算公式,虽计算简便,但推导较复杂.HUANG Zhiheng[5]等提出的重心插值推理方法,通过确定隶属函数的重心、位移参数与尺度参数进行推理,是目前被研究较多的方法.除此之外,刘文远[6]等提出了基于核集与相似性的模糊插值推理方法.文献[7]~文献[9]提出了基于排序和相似度度量的自适应模糊插值.
由于在模糊推理实际应用中,各因素状态几乎都是实数变量,因素所表现的模糊状态也都是模糊数.受以上研究启发,基于笔者提出结构元理论[10],提出新的稀疏规则库插值推理方法.该方法在保证推理结果正规性与凸性的基础上,避免了用α-截集方法求得结果,并使得推理运算更为简便.
1 预备知识
1.1 KH插值推理方法
已知的推理规则是模糊推理的依据,规则越丰富,对给定小前提的推理结论越容易产生.稀疏模糊规则库就是推理前件因素不能覆盖整个前提论域,以如下的模糊推理为例.
规则1 如果天气温度是热的,则电风扇是畅销的.
规则2 如果天气温度是凉的,则电风扇是滞销的.
小前提 现在的天气温度是正常的 结论 则电风扇是?
上述的推理可以表述为
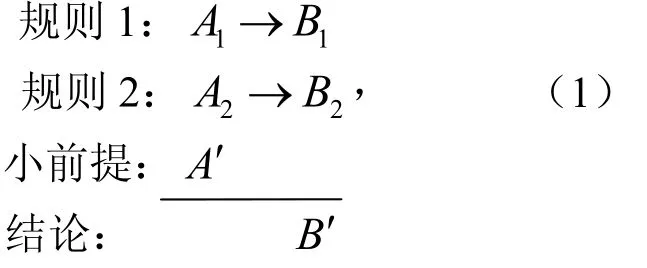
式中,A1,A2,A′为论域X上的一组有序模糊集,B1,B2,B′为论域Y上的有序模糊集,有A′≠A1,A′≠A2且A1<A′<A2.
当小前提与已知规则的前件没有重叠部分时,称推理规则是稀疏的,传统的模糊推理方法无法产生出结论,KOCZY和HIROTA[2]提出的KH线性插值推理方法就是试图解决这类问题.
所谓线性插值推理,就是按照模糊集距离的比例关系,来确定推理结论B′的方法.

假定论域X上的两个模糊集A1和A2有序关系A1<A2,A1和A2的α-截集(α∈[0,1])A1α和A2α之间的的上限距离dL和下限距离dU分别定义为
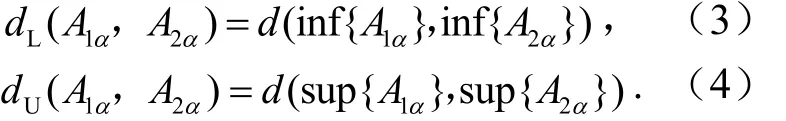
根据模糊集分解定理,式(2)被重写为
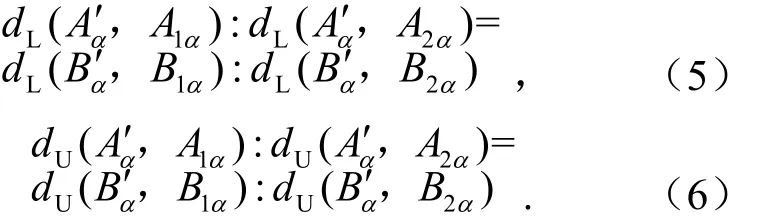
将式(3)、式(4)分别代入到式(5)、式(6)中得
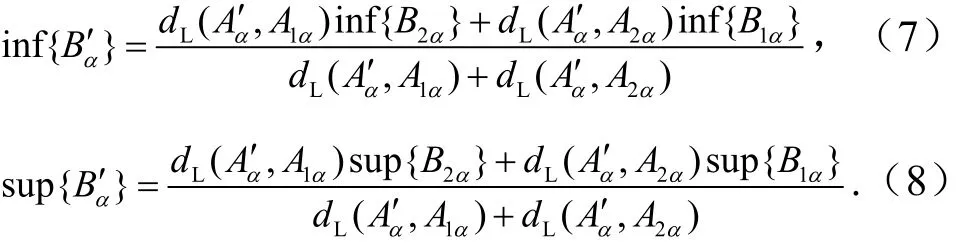
然而,在一些情况下,由此得到的推理结论B′不是一个正规凸模糊集,见图1.
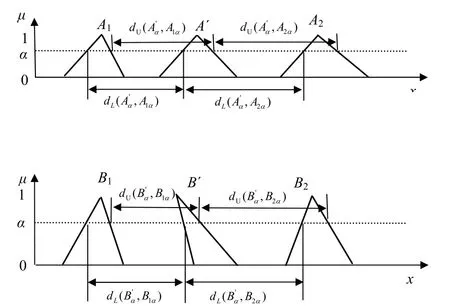
图1 KH插值推理方法不合理的结论 Fig.1 unreasonable conclusions of KH interpolation inference method
1.2 模糊结构元与模糊数
定义1设E是实数域R上的模糊集,其隶属函数记为E(x),x∈R.若满足下述性质.
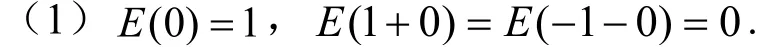
(2)当 -∞<x<-1 且1 <x<+∞时,E(x)=0.
(3)在区间[-1,0)上,E(x)是单增右连续函数,在区间(0,1]上E(x)是单降左连续函数,则称模糊集E为R上的模糊结构元[10].
若满足E(x)=E(-x),则称E为R上的对称型模糊结构元.
称模糊集E为三角结构元,若具有隶属函数

定理1(局部映射原理)设E是R上的任意模结构元,具有隶属函数E(x),又设函数f(x)在区间[-1,1]上是单调有界的,(x)是f(x)的延拓集值函数,则(E)是R上有界闭模糊数,且(E)的隶属函数为E(f-1(x)),这里f-1(x)是f(x)关于变量x和y的轮换对称函数(若f(x)是连续严格单调的,则f-1(x)是f(x)的反函数).在不引起混淆的情况下,记(x)为f(x)[10].
定理2(模糊数的结构元表现定理)对于给定的正则模糊结构元E和任意的有界闭模糊数A,总存在一个在[-1,1]上的单调有界函数f,使得A=f(E)[10].
在模糊插值推理中,常用三角模糊数与梯形模糊数,下面具体给出它们的结构元表达形式.
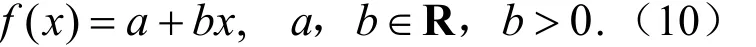
(1)A=f(E)是对称三角模糊数,取E为三角结构元,f(x)为 用特征点法表示A,记A=(α0,α1,α2),见图2(a),则a=α1,b=α1-α0.
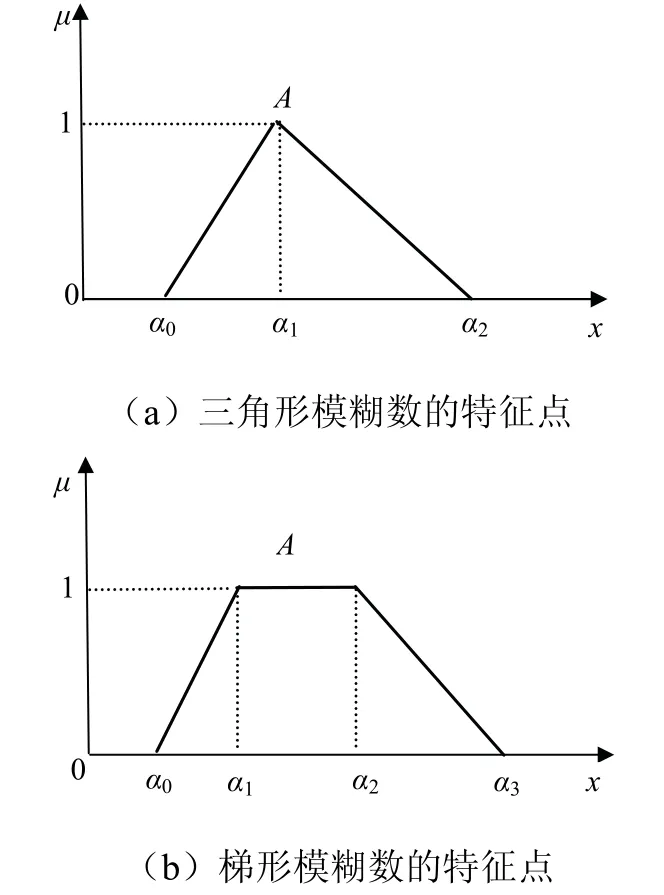
图2 三角形与梯形模糊数的特征点 Fig.2 characteristic points of triangle and trapezoid fuzzy numbers
(2)A=f(E)是非对称三角模糊数,取E为三角结构元,f(x)表达为

用特征点法表示A,记A=(α0,α1,α2),见图2(a),则
(3)A=f(E)是梯形模糊数,取E为三角结构元,f(x)表达为

若a<c,b=d,A=f(E)为对称梯形模糊数;若a<c,b≠d,A=f(E)为非对称梯形模糊数.
用特征点法表示A,记A=(α0,α1,α2,α3),见图2(b),则a=α1,b=α1-α0,c=α2,d=α3-α2.
2 基于结构元方法的模糊插值推理
由于推理结果B′对应的单调函数恒是递增的,所以基于结构元理论的模糊插值推理方法保证了推理结论隶属函数的凸性与正规性.将模糊数的运算利用结构元理论转换为单调函数的运算,无需分别求上限距离与下限距离,并且避免了用α-截集的方法求得结果,简便了推理运算.
在模糊插值推理中,推理规则前件与后件模糊集A与B常为语言变量值,且这些语言变量多用实数域中的模糊数进行表示,下面给出具体算法的描述.
2.1 模糊数的线性运算与距离
由模糊结构元理论知[9],设E是一个模糊结构元,f(x)和g(x)是[-1,1]上两个同序单调函数,使得模糊数A=f(E),B=g(E),则有
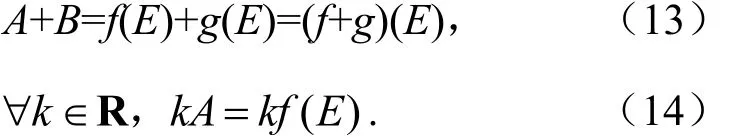
例1设A,B为对称三角模糊数,选取三角模糊结构元E,模糊数A,B可用结构元E线性表达,即存在实数a1,b1,a2,b2,使得A=a1+b1E,B=a2+b2E,则
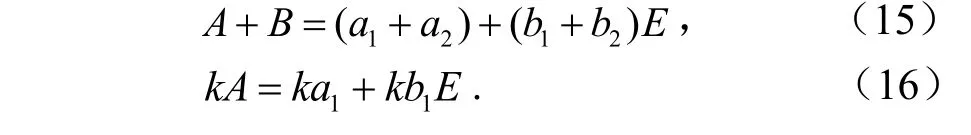
基于结构元理论,定义一种模糊数距离.
定义2设E是一个模糊结构元,f(x)和g(x)是 [-1,1]上两个同序单调函数,使得模糊数A=f(E),B=g(E),定义模糊数A,B的距离为

式中,D= max{f(1),g(1)} - min{f(-1),g(-1)}为f(x)和g(x)域值.
容易证明,式(17)满足距离的3条公理,此处证略.
取E为三角结构元,可以得到模糊插值推理中常用的三角模糊数与梯形模糊数距离公式.
(1)设A=f(E),B=g(E)为对称三角模糊数,
其中f(x)=a1+b1x,g(x)=a2+b2x,这里a1,b1,a2,b2为实数,b1>0,b2>0,则模糊数A,B的距离为
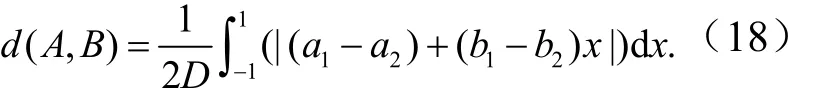
式中,D= max{(a1+b1),(a2+b2)} - min{(a1-b1),(a2-b2)}.
(2)设A=f(E),B=g(E)是非对称三角模糊数,
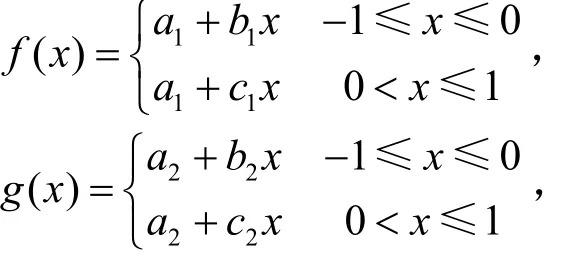
式中,a1,b1,a2,b2,c1,c2为实数,b1>0,b2>0,c1>0,c2>0,则模糊数A,B的距离为

(3)设A=f(E),B=g(E)是梯形模糊数,
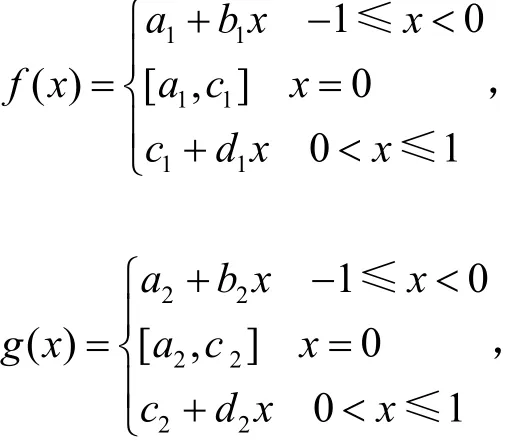
式中,a1,b1,a2,b2,c1,c2,d1,d2为实数,a1≤c1,a2≤c2,b1≥0,b2≥0,d1≥0,d2≥0,则模糊数A,B距离为

2.2 单维插值推理
给定式(1)的推理模型,其中,A1,A2,A′和B1,B2,B′分别为推理前件论域X和结论论域Y上的模糊数,且A1<A′<A2.
取三角结构元E,隶属函数见式(9),模型中模糊数可表示为A1=f1(E),A2=f2(E),A′=f0(E),B1=g1(E),B2=g2(E).在式(18)至式(20)中,根据模糊数的类型选取对应的公式,求出小前提与各规则前件的距离.根据两个模糊规则之间的线性插值定义为

可得
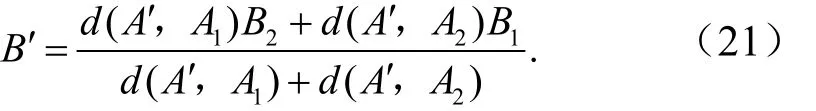
由式(14)可知,式(21)可转化为对应单调函数的运算
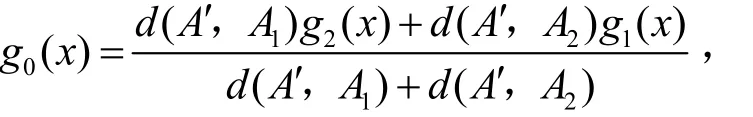
记

则
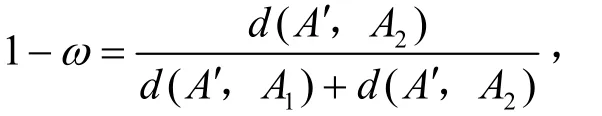
于是有
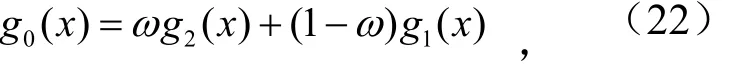
则B′=g0(E),具有隶属函数
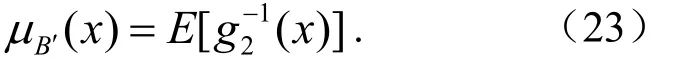
2.3 多维插值推理
上述方法可推广到多维插值推理模型中.假设推理前件存在m个推理变量fk(k=1,…,m),推理后件为一个结论变量v,已知n条由数据挖掘等方法得到的推理规则.变量fk与变量v的状态集为实数集合Xk与Y,Ak’与Aki(k=1,…,m;i=1,…,n)为Xk上的模糊数,B’与Bi=(i=1,…,n)为Y上的模糊数.
多维模糊插值推理结构写成如下推理形式.
规则1 若f1是A1n且f2是A21且…且fm是Am1,
则v是B1.
规则2 若f1是A12且f2是A22且…且fm是Am2,
则v是B2.
……
规则n若f1是A1n且f2是A2n且…且fm是Amn,则v是Bn.
小前提 若f1是 1A′且f2是 2A′且…且fm是mA′,结论g是B′.
将其简写为
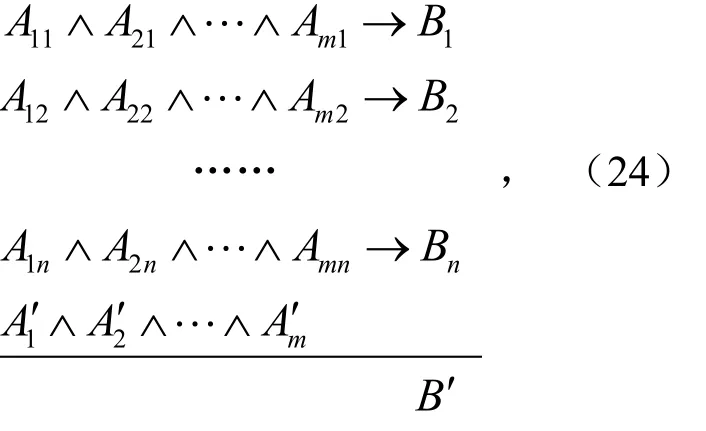
特别说明的是,在推理模型中不存在前件相同而结果不同的推理规则.
取三角结构元E,则推理模型中的模糊数可表示为Aki=fki(E),Ak0=fk0(E),Bi=gi(E),B′=g0(E)分别计算小前提与各条规则推理前件距离di(i=1,···,n).
先求前件中每个变量取值之间的距离
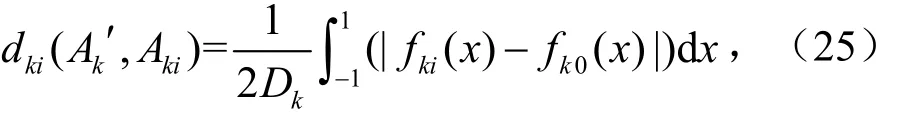
再求
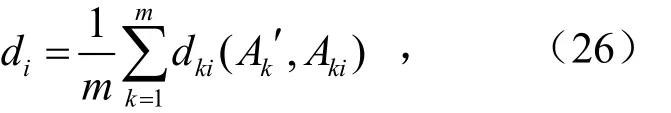
式中,
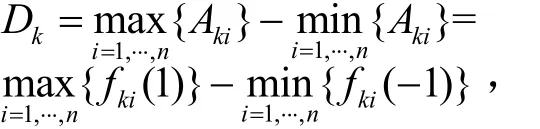
为第k个前件变量fk的域值.
给定阈值τ,选出距离小于τ的s(2≤s≤n)条规则进行下一步骤的计算.
记距离小于τ的s条规则为R1,…,Ri,…,Rs,利用第一步求得的小前提与各条规则推理前件的距离di,计算Aki的权重kiw′∈[0,1].权重计算方法如下
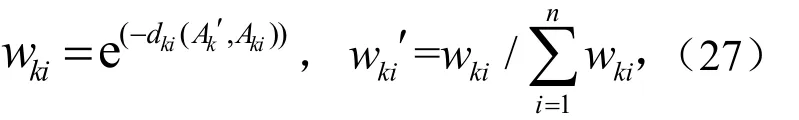
计算插值推理结论
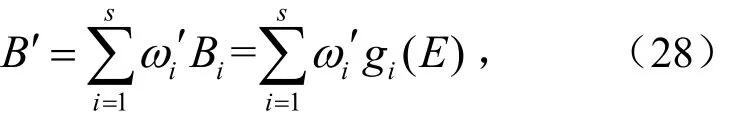
式中,
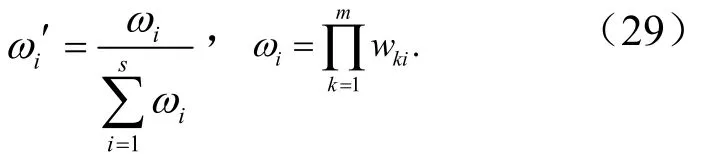
3 算例
下面以对称三角模糊数为例,说明多维插值推理方法的计算过程.设推理规则见表1.
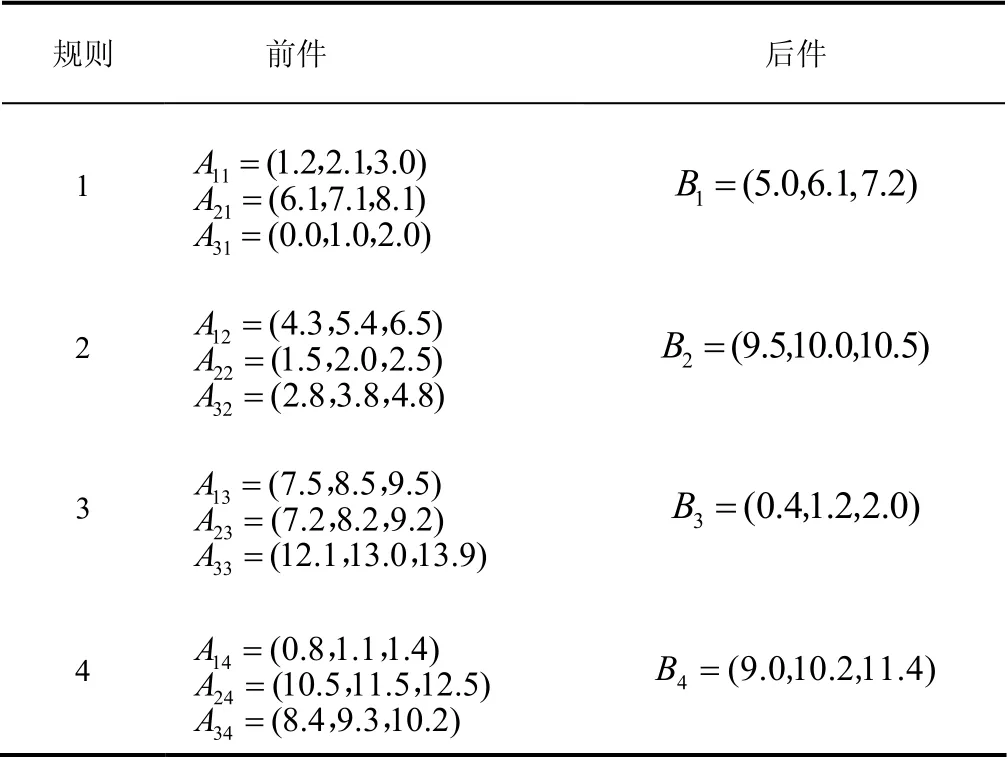
表1 已知规则 Tab.1 known rules
取三角结构元E,利用模糊数的结构元表示方法,表1所示的推理规则也可以表示为表2形式.
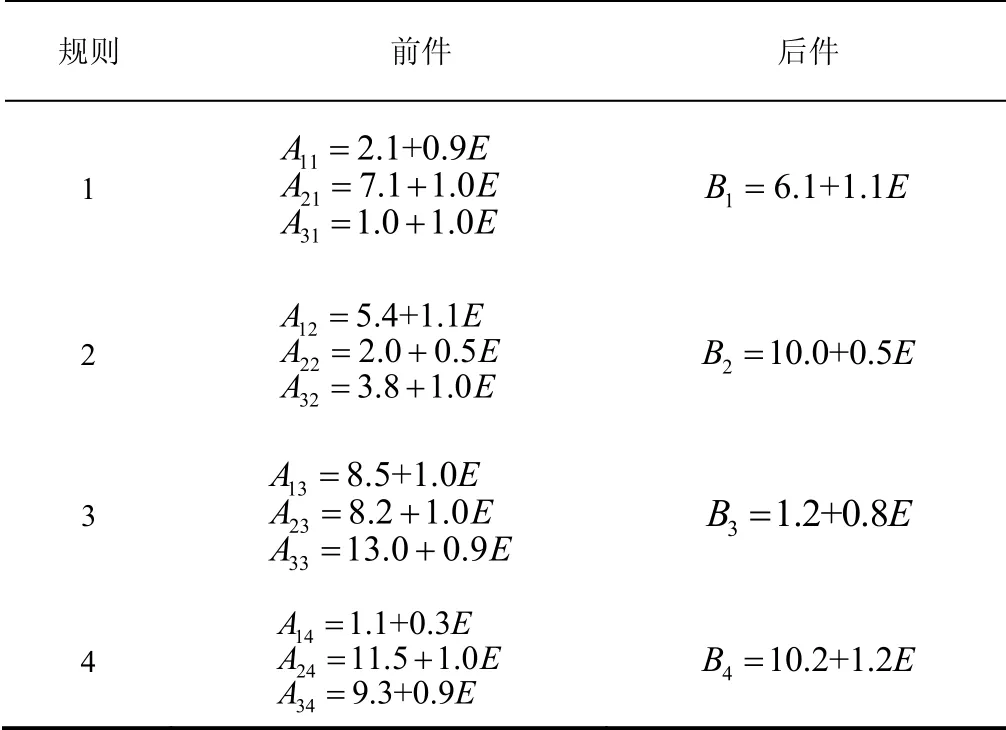
表2 已知规则的结构元表示 Tab.2 structural element representations of known rules
其结构元表示为
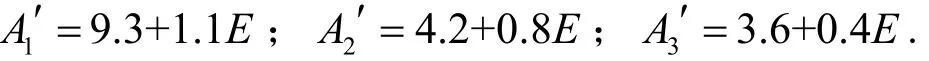
利用式(17),得到小前提与各条规则推理前件的距离分别为d1=0.282 2,d2=0.143 0,d3=0.315 6,这里取τ=0.3,则距离小于τ规则为2条,分别为规则1与规则2.
根据式(29)计算后件B1,B2的权重为
则推理的结论为
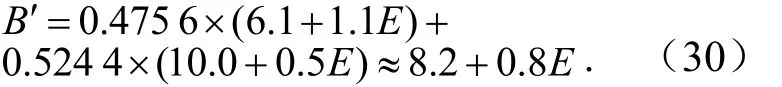
用特征点法表示为B′=(7.4,8.2,9.0).
4 结论
(1)基于模糊结构元理论定义了新的模糊数距离公式,构造了单变量与多变量的稀疏规则库插值推理方法.
(2)给出多变量情况下的算例,证明该方法保证了推理结果的正规性与凸性,避免了用α-截集的方法求得推理结论,简化了推理运算,并降低了推理运算的复杂度.

